При разработке упрощенной теории сейсмической дифракции А. Трореем за основу был взят дифракционный интеграл Гельмгольца, который выражает значение упругого потенциала j _p (или преобразования Лап­ласа от потенциала j _p) поля отраженных волн в произвольной точке р, расположенной внутри замкнутой поверхности S, через заданный на этой поверхности потенциал j _S :

,                                                   (4.3)

где j_р – преобразование Лапласа от скалярного потенциала поля отражен­ных волн в точке р внутри замкнутой поверхности S; r – расстояние от р до элемента DS на S; п – внешняя нормаль к S; V – скорость; р – транс­форманта Лапласа; j _S – заданный на S потенциал.

Данное уравнение имеет место лишь в рамках акустического прибли­жения, поэтому его решение содержит только продольные волны.

Трансформируя поверхность S в полусферу с бесконечным радиусом, на диаметральной плоскости которой расположен отражающий элемент, и аппроксимируя отражающую поверхность набором плоских полос бес­конечной длины и шириной Dx=x₂ – x ₁ (рис. 10, а), А. Трорей получил решение дифракционного интеграла (4.3) для одной[1] такой полосы в виде

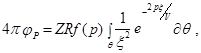                                                                                  (4.4)

здесь R – коэффициент отражения; f(р) – преобразование Лапласа от импульса волны в источнике Q; смысл обозначений Z, q  и x ясен из рис. 10. a. Для интегрирования выражения (4.4) следует выразить x через угол q (рис. 10, a), однако два важных вывода можно сделать и до этого

1. На каждом краю отражающего (дифрагирующего) элемента (в точ­ках А рис. 10, б) фаза дифракции изменяется на 180°. В самом деле, пусть D₁ и D₂ – результаты интегрирования (4.4) в направлении линии АВ (рис. 10, а) на расстоянии Х₁ и Х₂ соответственно (в пределах от -p/2 до p/2). Тогда j_р=D₂- D₁. Если Х₁<0, что соответствует положению точки p над полосой, то j_р=V–D₂– D₁ (здесь V обозначен член, соот­ветствующий отражению). Отсюда следует, что D₂ меняет знак при перехо­де Р через край полосы.

2. На дифрагирующем краю форма отраженной и форма дифрагированной волн совпадают, но величина амплитуды дифрагированной волны в 2 раза меньше. Действительно, пусть точка Р при движении слева направо пересекает дифрагирующую полосу (рис. 10, б). Для распространения алгоритма Трорея на случай многослойной среды с криволинейными Распределение амплитуд показано на этом же рисунке. Из условий непрерывности j_р при переходе через край А имеем D₂=V– D₂, т.е. D₂=V/2, что и требовалось.

3. Границами раздела, с горизонтальным градиентом плас­товых скоростей и плотностей, с угловыми несогласиями и выклиниваниями Ф. Хилтерман предложил вычислительный способ приведения среды над каждой границей поочередно к однослойной с единой постоянной скоростью. Для этой цели из каждого пункта наблюдения с равным шагом по углу производится трассирование лучей в исходной модели, после чего каждый прослеженный луч заменяется прямолинейным лучом, выхо­дящим из пункта наблюдения под тем же углом (рис. 10, в). Мнимое положение края плоского элемента рассчитываемой границы с номером j находится на прямолинейном луче на расстоянии, равном 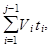 где V _i – локальная скорость; t_i – время прохождения трассированного луча в i-м слое (соответствующий пример представлен на рис. 10, в для границы 3). Множество всех полученных таким образом мнимых точек образует мни­мую модель, состоящую из одной границы с одной постоянной скоростью. От всех краев плоских элементов, составляющих эту мнимую границу, дифрагированные волны правомерно рассчитывать по "простой теории" Трорея.