Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Глава 1. Общие принципы интерпретации данных сейсморазведки на основе математического моделирования

Глава 2. Способы построения сейсмических моделей геологических сред

Предметом нашего рассмотрения являются волновые поля, образую­щиеся в многослойных средах в случае применения источника, возбуж­дающего преимущественно продольные волны, наблюдения отраженных волн при достаточно малых углах падения на границы раздела и регистра­ции только вертикальных компонент смещения. При моделировании таких волновых полей достаточно задавать в слоях модели следующие пара­метры: скорость продольных волн V_p, плотность s и коэффициент погло­щения продольных волн a _p. Поле продольных отраженных волн будет определяться в этом случае только данными параметрами, а распределение параметров поперечных волн не будет играть существенной роли. Вслед­ствие допущения о малых углах падения волны на границы раздела анизо­тропия скоростей также не учитывается.

В большинстве случаев для построения двумерных моделей использует­ся информация двух видов: высокоточная, но разреженная по площади геолого-геофизическая информация по разведочным скважинам и менее точная, но существенно более плотная сейсмическая информация между скважинами. Первая позволяет получить достоверные оценки физических свойств разреза в отдельных точках, т. е. построить одномерные модели. С помощью второй информации осуществляется переход к двумерным моделям.

Раздел 2.1. Построение одномерных моделей

Исходная информация, т. е. значения детальных скоростей и плотностей, для построения одномерных тонкослоистых моделей может быть получена несколькими способами:

1. По данным акустического (АК), гамма-гамма (ГГК) или гравита­ционного каротажей после соответствующей их обработки; обработка АК обычно включает процедуры вычисления скоростей с учетом кавернометрии, коррекции полученных скоростей по сейсмическому каротажу (СК), осреднения и др.; ГГК дает сразу плотность, поэтому обработка его заключается только в осреднении.

2. При отсутствии АК или ГГК, а также при низком их качестве акусти­ческие свойства разреза прогнозируются с использованием других широко рас­пространенных промыслово-геофизических характеристик: кажущегося сопротивления (r _k), интенсивности первичного (ГК) и вторичного (НГК) гамма-излучения и др.

3. Для приближенного задания акустических параметров тонких слоев иногда используются нормальные или обобщенные зависимости скорости и плотности от глубины для пород различной литологии.

Кроме того, информация о детальном распределении скоростей и плот­ностей в разрезе может быть получена по данным изучения керна, однако эти данные следует использовать только в тех случаях, если измерения про­водились в условиях, близких к пластовым.

Из перечисленных способов предпочтение следует отдать использованию данных АК и ГГК.

Осреднение данных АК и ГГК

Большое количество данных АК, накоп­ленное к настоящему времени, подт­верждает представления о тонкослоистой структуре реального скорост­ного разреза. Практически все осадочные породы, за редким иск­лючением (чистая соль, лед), имеют тонкослоистую структуру с той или иной степенью скоростной дифференциации.

Исходные непрерывные скоростные и плотностные разрезы, характеризующиеся высокой детальностью, не могут быть приняты в качестве одномерных моделей, по которым в дальнейшем предстоит построить двумерную модель. Тем или иным спосо­бом производится их осреднение и построение максимально упрощенной од­нородно-слоистой (или тонкослоистой) модели среды. Такая модель представляется в виде серии тонких однородных пластов, разделенных гра­ницами первого рода. При построении тонкослоистых моделей предпола­гается, что акустическая неоднородность, обусловленная внутренней измен­чивостью пород пласта, незначительна по сравнению с межпластовой акусти­ческой неоднородностью, связанной с изменением литологии или типа насыщения.

Способ осреднения с порогом. Применение его позволяет получить тонкослоистую модель в виде серии однородных слоев большей мощности по сравнению с исходным разрезом. Все границы в модели представляются границами первого рода. Сущ­ность алгоритма осреднения в данном способе заключается в том, что по заданным DV – величине значимой скоростной дифференциации и Dq_min – минимальной временной мощности слоев из разреза исключаются тонкие слои, время пробега в которых d t_i < Dq_min, объединяются слои с номера­ми i и i-1, если разница скоростей в них удовлетворяет условию

|V_i – V_i–1| £ DV

Значение скорости в объединенном слое вычисляется как среднее из V _i и V _i-1. Пороговое значение скачка скорости DV может быть различным для разных частей разреза.

Изменяя DV, можно менять число слоев в модели N, так как оно тем меньше, чем больше DV. Это может быть использовано для автоматическо­го поиска моделей с числом слоев, находящихся в заданных пределах N_min – N_max.

Методика полевых наблюдений

Как известно, требования повышения отношения сигнал/помеха и увеличения разрешенности записи в какой-то мере противоречивы. Поэтому на практике важно определить, какое из этих требований является доминирующим при изучении того или иного геологического объекта. Например, при изучении рифогенных построек, грабенообразных прогибов и др. прежде всего нужно обеспечить высокое отношение сигнал/помеха, а при выявлении зон выклинивания и страти­графического несогласия, первостепенным становится требование высокой разрешенности сейсмичес­кой записи.

На поисковом этапе исследований, в целях выявления рифогенных образований, грабенообразных прогибов, выступов кристаллического фундамента методика полевых работ может быть близка к производственной или отличаться от нее некоторым увеличением мощности интерференционных систем при возбуждении и приеме. Основные элементы такой методики следующие:

1) плотность сети профилей 1,5–2,0 пог. км на 1 км²;

2) схема наблюдения – в основном центральная;

3) кратность перекрытия 12 или 24;

4) максимальное расстояние взрыв – прибор Х_max = 1700–2500 м;

5) вы­нос 25–200 м;

6) расстояние между каналами 40–50 м;

7) группирование сейсмоприемников до 36 на канал, причем расположение приемников в одну или две линии на базе не более 50 м;

8) возбуждение – взрывы в одиночных скважинах с опти­мальной глубины или из группы мелких (4–5 м) скважин на базе не более 40–50 м.

При детальных исследованиях требования к методике полевых наблюде­ний повышаются и сводятся к следующему.

1) плотность профилей должна быть не менее 3 пог. км на 1 км², причем при детализации, например, грабенообразных прогибов большую часть профилей следует ориентировать вкрест прогиба с расстоянием между ними не более 500 м;

2) в целях повышения пространственной разрешенности расстояние между каналами не должно превышать 25–30 м;

3) группирование сейсмоприемников увеличивается до 48–60 элементов на канал, причем эти элементы располагаются по площади в виде 4–5 парал­лельных ниток; база группы должна быть не более 50 м.

Методика цифровой обработки

Независимо от содержания решаемой геологической задачи методика обработки должна предусматривать полу­чение временных разрезов с сохранением истинных амплитуд, с высокой разрешенностью отражений, с высоким соотношением сигнал/помеха, а также обеспечивать возможность высокоточного определения интерваль­ных скоростей.

Выполнение указанных требований достигается при использовании усложненного графа обработки, содержащего следую­щие процедуры:

1) демультиплексация цифровых записей (DMXT);

2) редакция (REDX);

3) коррекция амплитуд за геометрическое расхож­дение и поглощение (RAMP);

4) вычитание среднескоростных волн-по­мех (RECON);

5) минимально-фазовая деконволюция исходных записей (DECVTX);

6) широкополос­ная фильтрация исходных записей (FILVTX);

7) коррекция амплитуд за неидентичность условий возбуждения и приема (NORM);

8) коррекция статических поправок (SUMLAK);

9) коррекция кинематических поправок (сканирование или вертикальные спектры, KINVC);

10) автоматическая коррекция статических поправок (PAKS);

11) накапливание по ОГТ (SUMLC);

12) погоризонтный анализ скоростей (горизонтальные спектры скоростей, HORSP);

13) неза­висимая потрассовая коррекция остаточных фазовых сдвигов в несколь­ких временных окнах (WINCOR);

14) когерентная фильтрация (AMCOD);

15) нуль-фазовая деконволюция по раз­резу (ZEDEC);

16) широкополосная фильтрация по раз­резу (FILVTX);

17) когерентная фильтрация (AMCOD);

18) ми­грация (MIGFK);

19) псевдоакустический каротаж (РАК).

Раздел 3.2. Выбор способа решения прямой
динамической задачи

При использовании математического моделирования для целей интер­претации сейсмических данных возникает вопрос о выборе способа вычисления теоретического волнового поля. В последнее время для двумерного моделирования получили распространение способы, осно­ванные на лучевом приближении, и более точные способы, базирующиеся на решении дифракционного уравнения Кирхгофа или волнового уравнения в конечных разностях. Выбор способа является, прежде всего, вопро­сом методическим. Однако нельзя забывать и о стоимостной стороне дела, поскольку затраты машинного времени при вычислениях по точным спо­собам, например по алгоритму Трорея – Хилтермана, для некоторых, даже не очень сложных моделей, могут быть на один-два порядка выше, чем при вычислениях в лучевом приближении. Особенно остро вопрос о выборе способа вычислений стоит при использовании моделирования в итеративном режиме, когда предполагается многократное вычисление СВР.

При выборе способа его вычисления естественно исходить из того клас­са сейсмологических моделей, который предопределен решаемой при интерпретации геологической задачей. Зафиксировав этот класс моделей, нужно соотнести его с наиболее существенными допущениями, на которых построены конкретные вычислительные алгоритмы. Отправными здесь являются следующие соображения. Теория распространения сейсмических волн на основе лучевых представлений геометрической сейсмики предпо­лагает, прежде всего, абсолютную локальность сейсмических лучей, что равносильно утверждению о бесконечно малой длине волны, а также рас­пространение энергии волны по лучу и зеркальное ее отражение в един­ственной точке. Согласно волновым представлениям, полная энергия сейс­мической волны есть результат суммирования элементарных волн, при этом в одну и ту же точку приема приходит энергия, отраженная от неко­торого участка границы, которая, таким образом, должна иметь опре­деленную протяженность. Вследствие этого возникают явления дифракции, благодаря которым у окончаний границ не наблюдается резкого обрыва отраженных волн. При падении плоской волны на границу, содержащую резкие перегибы, их экстремальные точки являются источниками дифрагированных волн. Эти и некоторые другие явления не могут быть рассчитаны в лучевом приближении.

Для оценки величины области формирования отраженного импульса обычно используется параметр первой зоны Френеля F, который рассчи­тывается по известной формуле:

,

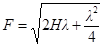где Н – глубина залега­ния отражающей границы; l – длина волны. Если протяженность отра­жающего элемента, связанного с какой-либо неоднородностью в геологи­ческом разрезе, составляет величину F зоны Френеля и более, то этот эле­мент отобразится на временном разрезе с максимальной амплитудой, со­ответствующей отражению от бесконечно длинной границы. При уменьше­нии горизонтальных размеров элемента (меньше F) он будет отображать­ся на временном разрезе с заметным уменьшением амплитуды, все мень­ше походить на отражение и все больше приобретать вид дифракции, со­ответствующей отражающей точке.

В связи с этим для практики моделирования большое значение имеет определение хотя бы примерного набора структурных и стратиграфических моделей, для которых ограничения лучевой теории могут оказаться неприемлемо жесткими и для построения СВР потре­буются способы, основанные на волновой теории. Далее рассмотрим примеры таких моделей, причем выбранные модели соответствуют геологи­ческим объектам, нередко обнаруживаемым в Волго-Уральской нефтегазоносной провинции. Для каждой модели вычислялись СВР по двум программам: по программе, алгоритм которой осно­ван на лучевых представлениях, и по программе, реализующей численное решение ди­фракционного уравнения Кирхгофа.

В первой программе СВР вычисляется путем поиска траекторий нормаль­ных лучей для заданных пунктов взрыва-приема (ПВП) и определения амплитуд отраженных волн. В осно­ву алгоритма второй программы положена простая теория дифракции А. Трорея, которую модифицировал Ф. Хилтерман для случая многослой­ной среды.

Пример 1. Моделирование микрограбенов

Данный пример (рис. 5) иллюстрирует отличие волновых полей от грабенообразных прогибов при различной их ширине. Последняя варьировалась, исходя из величины зоны Френеля, которая для модели на рис. 5, а при видимой длине волны l = 160 м и глубине границы Н = 2400 м составляет F = 880 м. Поэтому шири­на грабенов была задана следующей: l₁ = 0,5F = 440 м, l₂ = F = 880 м, l₃ = 2F = 1760 м.

На временных разрезах, полученных в лучевом приближении (рис 5, б), можно видеть адекватное отображение всех элементов модели грабенообразного прогиба независимо от его ширины. На временных разрезах, полученных по алгоритму Трорея – Хилтермана, наблюдается отчетливая зависимость волновой картины от ширины грабена: при ширине грабена меньше зоны Френеля происходит перекрытие разрыва в отражающих границах за счет дифракции, и при l₁ = 0,5 F разрыв практически незаме­тен. Существование его можно обнаружить лишь по небольшой аномалии времени и по некоторому ослаблению амплитуд. Это надо учитывать при практической интерпретации временных разрезов, чтобы избежать непра­вильных выводов относительно ширины прогиба, пределов распростра­нения вверх по разрезу разрывных нарушений и самого существования прогиба.

Пример 2. Моделирование подрифовых горизонтов

 

Данный пример (рис. 6) иллюстрирует различие в отображении на временных разрезах плоских горизонтальных границ, расположенных глубже рифогенных обра­зований. На рис. 6, а представлена обобщенная модель рифогенного образования фамен-турнейского возраста, составленная на основе анали­за и обобщения сейсмогеологических материалов по большому количе­ству структур Самарской и Оренбургской областей, рифогенная при­рода которых доказана. На модели граница 8 соответствует кровле терригенных отложений девона, границы 4 и 5 – бобриковскому горизонту, границы 2 и 3 – верейскому горизонту, граница 1 – кровле жестких отложений. В рифогенных образованиях, расположенных между граница­ми 5 и 8, скорость 6000 м/с, во вмещающих породах – 5400 и 5500 м/с.

Из сравнения временных разрезов на рис. 6, б, в, прежде всего, видно появление на обоих разрезах ложных антиклинальных перегибов по гори­зонту 8 с амплитудой 20 мс, хотя на модели граница 8 была задана плоской и горизонтальной. Отличие заключается в том, что на временном разрезе, вычисленном с учетом дифракции (рис. 6, в), по горизонту 8 наблюдает­ся резкое уменьшение интенсивности записи на участках флексурообразного перехода от горизонтальной части к ложной антиклинали. Кроме того, флексурообразные перегибы явились источниками ложных (мнимых) дифрагированных волн. Данный пример должен предостеречь от ошибочной интерпрета­ции реальных временных разрезов, на которых встречены аномалии, подоб­ные приведенным на рис. 6, б по горизонту 8. Очевидно, такие аномалии можно принять за горстовидные структуры.

Лекция 5

Рассмотренные модели являются достаточно "трудными" для расче­тов по лучевому методу, но следует учитывать, что соответствующие этим моделям реальные геологические объекты в Волго-Уральской провинции составляют не более 10-20 % от общего числа нефтегазоперспективных объектов. Кроме того, сравнение результатов моделирования для ряда других, менее сложных моделей (антиклинальные складки и флексурообразные перегибы слоев, тонкослоистая пачка с нерезким изменением толщин слоев или с плавно выклинивающимся одним слоем, выступы кристаллического фундамента с выклиниванием слоев в примыкающих отложениях, верейские и довизейские врезы с нерез­кой морфологией и др.) показывает, что временные разрезы, рассчитан­ные в лучевом приближении и по волновой теории, практически идентичны. В связи с этим применение лучевого метода при модельных расчетах с целью интерпретации может быть достаточно широким и полезным. Однако если в моделях имеются такие элементы, как тектонические нарушения, неоднородности с горизонтальными размерами, меньшими зоны Френеля, резкие перегибы слоев с радиусом кривизны, меньшим длины волны, и если при интерпретации используются в количественной форме динамические характеристики записи (например, при решении задач ПГР), то следует пользоваться более точными методами.

Предварительная коррекция

 

На этапе предварительной коррекции осуществляется сравнительно грубый подбор параметров модели в диало­говом режиме. Наличие данного этапа позволяет не вводить каких-либо ограничений на величину отклонения параметров модели нулевого при­ближения от искомого решения. Но вместе с тем если при первой оценке сходства (визуальной или по НФВК) синтетического и реального времен­ных разрезов обнаруживается явное их несходство, то ставится вопрос об изменении модели в целом или о переходе к другой гипотезе о геологи­ческом строении разреза.

Методической основой предварительной коррекции являются следующие положения:

1) при коррекции используются данные о сравнительной чувствитель­ности динамических характеристик записи к изменению параметров тонко­слоистой модели, полученные с помощью метода статистических испыта­ний;

2) в целях ограничения области поиска глобального экстремума из пер­вого этапа исключается и переносится на второй этап коррекция двух пара­метров исходного импульса (р, j) и в некоторых случаях коррекция толщин слоев;

3) для коррекции систематического отклонения толщин или скоростей в слоях, выражающегося в растяжении или сжатии трасс синтетического разреза, применяются формулы, которые учитывают значения первона­чальной скорости и толщины слоя;

4) на каждом шаге коррекции используются результаты сравнения СВР и РВР по НФВК, которые в конце предварительной коррекции могут дополняться сравнением по частным критериям (графики амплитуд и энергий, частотные спектры и др.) или с помощью дифференциальной оценки сходства.

Рассмотрим подробнее перечисленные положения.

Лекция 6

Учет динамических факторов

Амплитуды отражений рассчитываются на основе следующих положений теории распространения волн:

1) непре­рывность напряжений и смещений для плоских волн, отражающихся от плоских границ;

2) сохранение энергии внутри лучевой трубки;

3) по­стоянный параметр поглощения Q, учитывающий минимально-фазовый механизм потерь при распространении за счет поглощения энергии.

Условия непрерывности на границе дают для коэффициента отражения простейшую формулу, строго справедливую в рассматриваемом случае нормального падения луча:

,

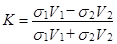где 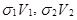 – акустические жесткости слоев, лежащих соответственно выше и ниже отражающей границы.

Для учета геометрического расхождения воспользуемся известной фор­мулой:

,

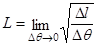где L – коэффициент геометрического расхождения; Dl – поперечный размер сечения лучевой трубки плоскостью паде­ния волны в точке наблюдения; Dq – интервал углов выхода, ограничи­вающий лучевую трубку. Обозначив R амплитудный фактор расхождения, с учетом соотношения R = L^-2

R= 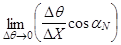,                                                                                               (4.2)

здесь Dq и DX – приращения угла засылки лучей и точек их выхода соот­ветственно; a _N – угол выхода нормального луча.

На основе формулы (4.2) построен итеративный алгоритм вычисления амплитудного фактора R, учитывающего геометрическое расхождение. Упрощенное описание его сводится к следующему.

Шаг 1. Засылка из данного пункта взрыва-приема пяти лучей с углами q _N-F, q _N‑F/2, q _N, q _N+F/2 и q _N+F и получение соответствующих точек выхода (F – малая величина порядка ~ 10^-4 – 10^-5, задаваемая в исходных данных).

Шаг 2. Формирование из пяти трассированных на шаге 1 лучей систе­мы из двух пар лучей так, чтобы каждая пара вмещала бы данный ПВП и чтобы одна из пар вмещала другую (см. рис. 9, б); вычисление двух значений амплитудного фактора R:

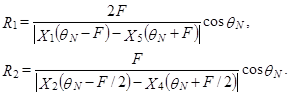
Шаг 3. Проверка предельного перехода

.

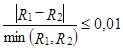Если "да", то R=R₂ и алгоритм заканчивается. Если "нет", проверяется условие |X₁‑X₅| < 50. При невыполнении этого условия расхождение считается вычисленным условно. В случае выполнения приращение увеличивается в 2 раза. Переход к шагу 1. При этом делается не более 16 попыток достигнуть сходимости в формуле (4.2) за счет увеличения F.

С учетом вышерассмотренных динамических факторов вычисляется импульсный временной разрез, в котором до свертки с заданным сейсми­ческим сигналом можно также произвести учет частотно-зависимого погло­щения сейсмической энергии.

Влияние фокусировки сейсмической энергии на амплитуду отраженных сигналов учитывается автоматически в ходе вычисления траекторий нор­мальных лучей. Явления фокусировки возникают при наличии локальных отрицательных перегибов в поведении границ (вогнутостей), когда нор­мальные лучи пересекаются (образуют каустики) в непосредственной бли­зости от линии наблюдения. Примером могут служить участки перехода от горизонтальной границы к крылу пологой структуры. В этом случае для одного и того же ПВП находятся два и более нормальных лучей с почти равными временами прихода отраженных сигналов которые автоматически суммируются.

Глава 1. Общие принципы интерпретации данных сейсморазведки на основе математического моделирования