P₅₀(30£ k £ 40)=Ф(x^// ) –Ф(x^/ )

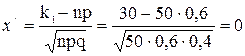; Ф(x^/ )=Ф(0)=0

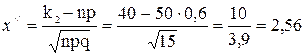;     Ф(x^// )=Ф(2,56)=0,4948

P₅₀(30£ k £ 40)=0,4948–0=0,4948

Когда требуется найти такое значение k₁, при котором вероятность наступление события А (Рn(k)) наибольшая, можно воспользоваться формулой

np–q£ k₀ £np+p

Пример 24. Вероятность попадания стрелком в мишень при одном выстреле 2/3. Каким будет наивероятнейшее число попаданий при 15 выстрелах?

Решение. p= ; q=1–p= ; n =15

15× – £ k₀ £15× +

30–1£3k₀                                     3k₀£32

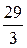£k₀                                            k₀£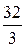

9,6£k₀                                                                          k₀£10,6

                          9£ k₀£10

Задания

20. 10 мощных ламп освещают съемочную площадку в Останкино. Съемка телесюжета идет 5 часов. Вероятность одной лампы выйти из строя за это время 0,4. Какова вероятность того, что 4 лампы из 20 за время съемки выйдут из строя?

21. Студент с вероятностью 0,8 решает задачу. Какова вероятность решить ему 3 задачи из 5?

22.  На склад поступили 6 приборов, из них 4 – II-го сорта. Какова вероятность взять потребителю наудачу 2 прибора II-го сорта?

23. Производится 5 подбрасываний игральной кости. Найти вероятность того, что цифра «6» появится хотя бы 2 раза.

24. Вероятность поражения стрелком мишени р=0,6 при одном выстреле. Найти вероятность того, что из 4х выстрелов стрелок поразит мишень не менее 3х раз.

25. К бензоколонке на заправку в течение дня подходит 100 автомашин. Из них 40 грузовых. За время t заправилось 10 автомашин. Какова вероятность того, что среди них окажутся две грузовые.

26. За смену станок производит 100 деталей. Из них 10 бракованные. Наудачу берут 7 деталей. Найти вероятность того, что хотя бы 3 из них будут бракованные.

27. На праздничном вечере разыгрывается 100 лотерейных билетов, из которых 60 выигрышные. Найти вероятность того, что у владельца 5 лотерейных билетов выигрышными окажутся не менее 3-х билетов.

28. Вероятность студенту взять 1 билет в театр «Оперы и балета» 0,5, а в драматический – 0,6. Студент хочет взять на вечер 2 билета. В театре «Оперы и балета» в кассе осталось 8 билетов, а в драматическом – 6. Какова вероятность студенту взять два билета в какой-либо театр?

29. Летчик поражает летящую учебную цель с вероятностью 0,9. Он делает 5 выстрелов. С какой вероятностью он поразит мишень хотя бы 3 раза из 5.

30. Два парашютиста выполняют прыжки с самолета . Вероятность приземлиться в обозначенное место для 1-го парашютиста – 0,8, для 2-го – 0,7. Первый совершает 5 прыжков, второй – 4. Какова вероятность 1му и 2му парашютисту приземлиться в обозначенное место не менее 2-х раз?

31. Цех завода выпускает за время t 200 ламп дневного света. Из них бракованными оказываются 20 штук. На повторный контроль отбирается 10 ламп. Какова вероятность того, что среди них окажется менее 2-х бракованных?

32. Подбрасываются 3 игральные кости 3 раза. Какова вероятность того, что цифра «6» выпадет на 1ой кости 2 раза; на 2ой – не менее 2-х раз и на 3ей – 1 раз?

33. Студент получит стипендию, если он сдаст все 5 экзаменов и из них на «отлично» не менее 3-х. Вероятность студенту сдать на «отлично» один экзамен равна 0,7. Какова вероятность того, что студент получит стипендию?

34. Предприятие начнет выпуск продукции, если оно поучит станки 2х видов. Причем станков I-го вида не менее 3х из 5, а II-го вида хотя бы 2 из 6 планируемых. Вероятность поставки станка I-го вида – 0,7, а II-го – 0,6. Какова вероятность предприятию начать работать?

35. Два стрелка стреляют по 2м различным целям и делают по 5 выстрелов. Вероятность поразить цель при одном выстреле для 1го стрелка – 0,6, для второго – 0,7. Найти вероятность того, что первый попадет в цель не больше 3х раз, а второй – не меньше 3х раз.

36. На склад доставили две упаковки с приборами в количестве 5 и 6 штук в каждой. Вероятность повреждения прибора в пути для первой упаковки 0,4, для второй – 0,3. Найти вероятность того, что при транспортировке оказались поврежденными 3 прибора 1ой упаковки и два второй.

37. В магазине продается живая рыба: форель и карпы в количестве 20 штук, среди которых карпов 6. Какова вероятность, что продавец выловит наудачу а) сразу 2х карпов; б) 2х карпов по очереди?

38. Группа студентов получает приз, если выйдет на первое место хотя бы по 2м из 3х показателей по успеваемости, по посещаемости занятий и по художественной самодеятельности. В группе по итогам сессии на положительные оценки из 25 человек сдало 20. По итогам посещаемости за семестр вероятность получить 1ое место составляет 0,7, а по художественной самодеятельности – 0,8. Какова вероятность выйти группе на 1ое место?

39. Система состоит из двух агрегатов, задействованных последовательно. Первый содержит 4 одинаковых, независимо работающих друг от друга блока, второй – 5. Вероятность выйти из строя одному блоку 1го агрегата 0,3, а для блока 2го агрегата – 0,2. в течении года система отключается, если какой либо агрегат выходит из строя. Первый агрегат отключается при выходе из строя одного блока. Второй – при выходе из строя двух блоков. Какова вероятность , что система в течение года отключится?

40. Игральный кубик подбрасывается 300 раз. Найти вероятность того, что цифра «5» появится 40 раз.

41. Вероятность появления события А в каждом из независимых испытаний равна 0,3. Найти вероятность того, что событие А наступает 80 раз в 300 испытаниях.

42. Станок штампует в смену 400 заготовок для болтов. Вероятность появления брака для каждого болта 0,2. Найти вероятность того, что брак появится у 50 болтов.

43. Вероятность появления события А в каждом из 2100 независимых испытаний равна 0,7. Вероятность того, что событие появится k раз равна 0,0189. Найти число k.

44. Партию телевизоров в 1000 штук завод доставляет на склад магазина. Вероятность повреждения в пути одного телевизора 0,001. Найти вероятность того, что в пути повреждено 3 телевизора.

45. Радиоэлектронная система содержит 3000 резисторов. Вероятность отказа каждого из них 0,0004. Какова вероятность отказа системы, если она выходит из строя при отказе хотя бы 2х элементов.

46. Два зенитных орудия стреляют по одной цели. Первое попадает в цель с вероятностью 0,6, а второе – с вероятностью 0,5. Сколько будет сделано залпов, при которых оба орудия попадут в цель, если общее число залпов равно 10?

47. Обувной цех в течение смены выпускает 300 пар обуви. Вероятность брака одной пары р=0,01. Какова вероятность того, что будет забраковано а) 3 пары обуви? б) не более 3х пар обуви?

48. Трикотажная фабрика выпускает перчатки, которые выборочно проходят ОТК. Вероятность одной паре перчаток не пройти ОТК равна 0,3. Какова вероятность того, что из 300 отобранных наудачу пар перчаток от 60 до 100 не пройдут ОТК?

49. Вероятность того, что на железнодорожном участке пути АВ при прохождении состава поезда произойдет авария равна 0,01. Найти вероятность того, что из 1000 составов , проходящих по этому участку за неделю безаварийно пройдут не больше 900 составов.

50. Вероятность появления события А в каждом из 24 независимых испытаний равна 0,6 . Найти вероятность того, что событие появится: А) не более 12 раз; б) менее 12 раз.

51. Выпущено120 лотерейных билетов. Из них 40 выигрышных. Сколько надо купить билетов, чтобы наивероятнейшее число выигравших билетов равнялось 5.

52.    100 штук футболок, выпущенных цехом, проходят ОТК. Вероятность для футболки быть забракованной равна 0,1. Найти наивероятнейшее число футболок, наудачу отобранных для ОТК, которые окажутся забракованными.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайная величина – отвлеченное выражение случайного события. Это величина, которая в результате опыта примет одно возможное, наперед неизвестное значение, зависящее от случайных причин. Случайную величину обозначают X, Y, Z, а ее количественные значения x_i, y_i, z_i (i = 1,…,n).

Если, например, x_1, x₂ …, x_n образуют дискретный ряд чисел, то X называется дискретной случайной величиной (ДCВ). Если же количественные значения заполняют промежуток (а,в), то X называется непрерывной случайной величиной (НСВ). Каждому значению случайной величины ставится в соответствие определенная вероятность его появления в опыте. Распределение вероятностей описывается законом. Для ДСВ Х это – ряд распределения, т.е. таблица, где каждому x_i соответствует определенное значение вероятности его появления p_i, причем x_i < x_i+1; и 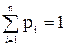. Графически это – многоугольник распределения.

Для непрерывной случайной величины характеристикой вероятности появления x_i в интервале (x; x+Dx) является плотность вероятности f(x)       (аналогично распределению массы вдоль Ох в механике, если она распределена по какому-то закону). Это неотрицательная функция и .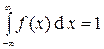

Функция плотности позволяет вычислить вероятность попадания НСВ Х в интервал (а,b), т.е.

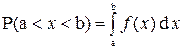
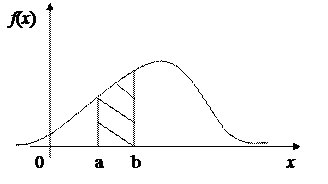Графически функция плотности напоминает «колокольчик», а вероятность попадания в заданный интервал есть площадь, ограниченная этой кривой на (a,b).

Зная ряд распределения или функцию плотности вероятности, можно построить соответствующую функцию распределения F(x). Ее еще называют интегральной функцией распределения, а f(x) - дифференциальной функцией плотности.