Выражения, определяющие вероятности суммы или произведения событий, зависят от того, совместны эти события или нет, зависимы они или нет.
События совместны, если могут произойти в данном опыте одновременно и несовместны, если это невозможно.
Пример9. 1. Событие А—появление туза, событие В появление карты пиковой масти. А и В —совместные события.
2. Событие А — появление двойки, событие В — появление четной цифры при бросании игральной кости. А и В—совместные события.
3. Событие А — попадание в мишень при первом выстреле. Событие В — непопадание в мишень при первом выстреле. События А и В —несовместны.
События А и В – независимы тогда и только тогда, когда на вероятность появления одного события не влияет появление другого. В противном случае события А и В называются зависимыми.
На практике о независимых событиях судят по смыслу задачи. Часто независимыми оказываются события, не имеющие одно к другому никакого отношения.
Пример10. Бросается 2 монеты. Событие А— на первой монете выпал «герб». Событие В — обе монеты упали одинаковым образом.
Решение. Всего четыре исхода опыта {ГГ, ГЦ, ЦГ, ЦЦ}.
Пусть А: {ГГ, ГЦ} 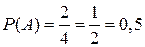
Пусть В: {ГГ, ЦЦ} 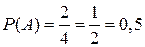
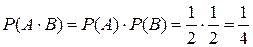
Действительно, пересечение событий А и В, т.е. 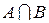 будет одно событие {ГГ}, т.е.
будет одно событие {ГГ}, т.е. 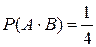 . Следовательно, события А и В независимы.
. Следовательно, события А и В независимы.
Теорема сложения (объединения) вероятностей несовместных событий: Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий. Для двух событий А и В:
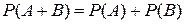 .
.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий. Так для n событий А i (i = 1, …,n):
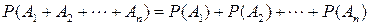 .
.
Если события A1, A2,…, An образуют полную группу, и попарно несовместны, то
P(A1) + P(A2) +…+ P(An)=1
Два события, образующих полную группу, называются противоположными.
Пусть событие А — попадание стрелка в цель, тогда противоположное событие 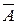 — промах стрелка.
— промах стрелка.
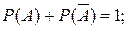
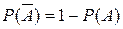
Теорема сложения вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий, безразлично какого, равна сумме вероятностей этих событий без вероятности их совместного появления. Для двух событий А и В:
P(A+B) =P(A)+P(B)–P(A×B).
Теорема умножения вероятностей двух независимых событий: Вероятность совместного появления двух независимых событий, равна произведению вероятностей этих событий.
P(A×B) =P(A)×P(B).
Для нескольких независимых событий
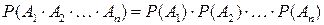 .
.
Теорема умножения вероятностей двух зависимых событий: Вероятность совместного появления двух зависимых событий, равна произведению вероятности одного из них (P(A)) на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило (PA(B)).
P(A×B) =P(A)×PA(B).
Аналогично, P(A×B) =P(B)×PB(A).
Вероятность совместного появления трех и более событий равна произведению вероятности одного из них на условные вероятности всех остальных:
P(A×B×C) =P(A)×PA(B)×PA B(C).
Пример 11. В урне 12 шаров, из низ 5 синих, остальные — белые. Наудачу берут 3 шара. Найти вероятность того, что
a) хотя бы один шар будет синим,
b) синих шаров взято не будет.
Решение. 1) Хотя бы один (событие А) означает, что один или два или три синих шара взято из урны.
Событие В —из урны взяты один синий и два белых шара.
Событие С —из урны взяты два синих и один белый шара.
Событие D —из урны взяты три синих шара.
A, B, C – события несовместные.
Тогда 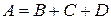
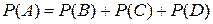
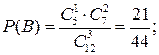
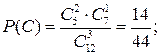
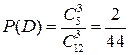
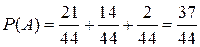 (по теореме сложения несовместных событий).
(по теореме сложения несовместных событий).
2) Взят хотя бы один синий и ни одного синего не взято — противоположные ( 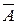 и А), следовательно,
и А), следовательно,
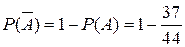
Пример 12 . Три стрелка стреляют по мишени и каждый делает по одному выстрелу. Вероятность попасть в мишень первому стрелку 0,9; второму — 0,7; третьему —0,8. Найти вероятность того, что в мишень попадет:
a) только один стрелок;
b) только два стрелка;
c) не попал ни один.
Решение. а) Событие А1 – попал первый стрелок; 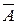 1 – не попал ;
1 – не попал ;
Событие А2 – попал второй стрелок; 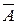 2 – промах ;
2 – промах ;
Событие А3 – попал третий стрелок; 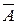 3 – промах.
3 – промах.
Событие А – попал только один стрелок. Это означает, что попал первый, а второй и третий промахнулись или попал второй, а первый и третий промахнулись или попал третий, а первый и второй не попали в мишень, т.е.
А = А1 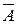 2
2 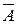 3+ А2
3+ А2 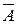 1
1 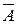 3 + А3
3 + А3 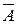 1
1 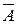 2.
2.
Здесь каждое из слагаемых есть произведение независимых событий, тогда Р(А) = Р(А1)Р( 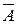 2)Р(
2)Р( 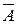 3) + Р(А2)Р(
3) + Р(А2)Р( 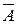 1)Р(
1)Р( 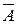 3) + Р(А3)Р(
3) + Р(А3)Р( 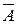 1)Р(
1)Р( 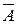 2).
2).
Р(А1) = 0,9 Р( 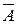 1) = 1– 0,9 = 0,1
1) = 1– 0,9 = 0,1
Р(А2) = 0,7 Р( 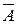 2) = 1– 0,7 = 0,3
2) = 1– 0,7 = 0,3
Р(А3) = 0,8 Р( 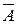 3) = 1– 0,8 = 0,2
3) = 1– 0,8 = 0,2
Р(А)= 0,9×0,3×0,2 + 0,7×0,1×0,2 + 0,8×0,1×0,3 = 0,092
б) Событие В — в цель попали только два стрелка
В= А1 А2 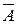 3 + А2 А3
3 + А2 А3 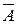 1+ А1 А3
1+ А1 А3 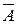 2
2
Р(В)= 0,9×0,7×0,2 + 0,7×0,8×0,1 + 0,9×0,8×0,3 = 0,398
с) Событие 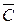 — в цель не попал ни один стрелок
— в цель не попал ни один стрелок
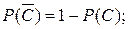 С= А1 А2 А3 Р(С)= Р(А1)Р( А2)Р( А3)
С= А1 А2 А3 Р(С)= Р(А1)Р( А2)Р( А3)
Р(С)= 0,9×0,7×0,8 = 0,594
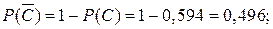
Пример13. Два стрелка стреляют по мишени и делают по одному выстрелу. Вероятность поразить цель первым стрелком равна 0,5; вторым — 0,7. Найти вероятность того, что в цель
1. попадут оба стрелка;
2. какой –либо один.
Решение . а) Событие С — в цель попадет и первый и второй стрелок.
Событие A — в цель попал первый стрелок;
Событие В — мишень поразил второй стрелок.
Так как события A и B независимы, то C = A×B и
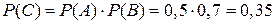
б) Событие D — в цель попал какой-либо один стрелок, т.е. попал или первый или второй, но не оба вместе D = A + B – A×B, т.к. A и B —события совместные, то
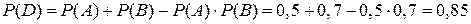
(по теореме сложения совместных событий)
Пример 14. В группе восемь девушек. Из них 5 — светловолосые. Наудачу выбираются одна за другой три девушки. Какова вероятность того, что все три окажутся светловолосыми?
Решение. а) Событие A — первая девушка светловолосая,
событие B — вторая девушка светловолосая,
событие C — третья девушка светловолосая.
Вероятность того, что первая девушка светловолосая
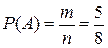
Так как число светловолосых девушек уменьшилось на единицу, т.е. их осталось 4, соответственно и общее число девушек уменьшилось на единицу, т.е. их осталось 7, то вероятность, второй отобранной девушке быть светловолосой, равна
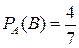
Рассуждаем аналогично, получаем
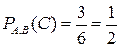
Тогда искомая вероятность, согласно теореме о произведении вероятностей зависимых событий (совмещенных) будет:
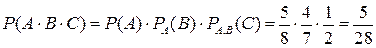
Пример 15. Вероятность попадания в первую мишень для стрелка равна 2/3. Если при первом выстреле стрелок попал, то он получает право на второй выстрел по другой мишени. Вероятность поражения первой и второй мишени при двух выстрелах равна 0,5. Какова вероятность поражения второй мишени?
Решение. а) Событие A — стрелок попал в первую мишень,
событие B — стрелок попал во вторую мишень.
Известно, что 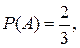

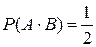 .
.
Но во вторую мишень он может попасть только при условии, что он попал в первую, тогда вероятность его попадания во вторую мишень есть условная вероятность 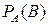 .
.
Дата: 2019-12-09, просмотров: 505.