Основные формулы комбинаторики
| Без повторения элементов | С повторениями (возвращениями) элементов |
| Перестановки | |
| P(n) = n! | 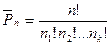 n 1 , n 2 , … nk — число повторений соответствующих элементов
n 1 , n 2 , … nk — число повторений соответствующих элементов
|
Размещения
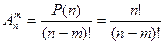
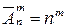
Сочетания
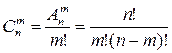
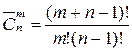
Пример 2. Найти число перестановок из трех цифр 1, 2, 3.
Решение. 123, 132, 231,213, 321, 312 или P3 = 3! = 1· 2· 3=6.
Пример 3. Найти число перестановок из букв слова «потоп».
Решение. P5 = 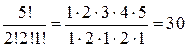 , так как в слове «потоп» 2 буквы «п», 2 буквы «о» и одна буква «т».
, так как в слове «потоп» 2 буквы «п», 2 буквы «о» и одна буква «т».
Пример4. Найти число размещений из четырех цифр 1, 2, 3, 4 по две.
а) без повторения цифр;
б) с повторениями их.
Решение. а) 12 13 14 21 23 24
31 32 34 41 42 43
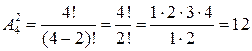
б) 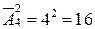
Пример 5. Найти число сочетаний из четырех элементов a , b , c , d по два
а) без повторения элементов;
б) с повторениями.
Решение. а) 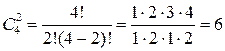
б) 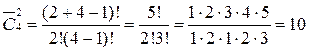
Здесь ab и ba неразличимы.
Замечание: В каждой конкретной задаче выбор формулы для подсчета m и n определяется ее содержанием.
Пример 6. На автодороге Красноярск–Дивногорск за время t зарегистрирован проезд 1000 автомобилей. Из них 6 инициировали дорожно-транспортные происшествия. Найти относительную частоту аварий автомобильного транспорта на этом участке.
Решение. Событие А—«произошло дорожно-транспортное происшествие». Тогда частота появления события А
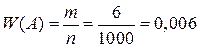
Пример 7. В урне a белых и b черных шаров. Наудачу выбирают три шара. Найти вероятность того, что они все черные.
Решение. Событие А—«вынуты 3 черных шара». Общее число равновозможных исходов испытания равно числу способов, которыми можно извлечь три шара из общего числа (a + b) шаров, т.е. числу сочетаний из (a + b) по 3: 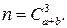
Найдем число исходов, благоприятствующих событию А: вынуть три черных шара. Так как черные шары можно взять только из черных, то число способов вынуть три черных шара равно числу сочетаний из b черных шаров по 3: 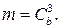
Тогда 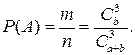
Здесь для подсчета m и n применили формулы сочетаний, так как порядок взятых трех шаров нас не интересует.
Пример 8. На отрезке [0,3] оси Ox называется произвольное число. Найти вероятность того, что оно будет принадлежать части этого отрезка [1,3].
Решение. Пусть событие А – «число принадлежит отрезку [1,3]». В задаче пространство всех равновозможных элементарных событий (G) имеет размер длины отрезка и равно 3, а пространство элементарных событий, благоприятствующих наступлению события А (g), равно 2 — длине отрезка[1,3].
Тогда 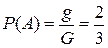
Задания
a) Человек решил поехать на день рождения к своему другу. Но к нему можно добраться только с пересадкой в городе А. Сначала у него есть три варианта поездки: поездом, автобусом пароходом, а дальше до места назначения только вертолетом или на моторной лодке. Сколькими способами человек может добраться к своему другу?
b) Сколько различных перестановок можно составить из букв слова «демократия», «крокодил»?
c) Сколькими способами можно разместить 8 человек в двух купе, если Нина и Оля должны быть в одном купе?
d) Проводник разносит пассажирам чай. В его распоряжении 9 купе по 4 человека в каждом. Сколькими способами он может обслужить их?
e) Серебренная, золотая и бронзовая медали разыгрываются между десятью штангистами. Сколькими способами медали могут быть распределены?
f) Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, если цифры
g) не повторяются
h) повторяются?
i) Сколькими способами можно распределить на пароходе среди шести человек
j) 3 одноместные каюты I класса?
k) Одну каюту «люкс», одну одноместную I класса и одну одноместную II класса?
l) Сколькими способами можно разместить на стоянке автомобилей на лучшее место сначала 2 «Нивы» из 5, потом 3 «Мерседеса» из 5, а затем остальные машины? Всего в очереди на размещение 16 машин.
m) В урне 5 белых и 4 красных шара. Сколькими способами можно достать 3 белых шара? Сколькими способами можно достать любые 3 шара?
n) На верхней полке в купе можно разместить 4 багажных предмета. Сколькими способами это можно сделать? Сколькими способами их можно расставить на двух верхних полках?
o) В магазине покупатель может приобрести для себя 10 различных предметов одежды. Сколькими способами он может купить 2 разные по составу комплекта одежды из 8 предметов?
p) Из 100 подбрасываний монеты «герб» выпал 48 раз. Какова относительная частота появления «герба»?
q) На испытательном стенде проходят проверку на виброустойчивость 100 приборов. Относительная частота годных приборов оказалась равной 0,93. Найти число бракованных приборов.
r) На работу проводником требуются пять человек. Подали заявление 8 человек, из них 5 женщин. Найти вероятность того, что будут отобраны двое мужчин и три женщины.
s) В соревнованиях по парному фигурному катанию на зимних олимпийских играх разыгрываются медали золотая, серебряная и бронзовая. В розыгрыше участвуют спортсмены из Англии, Финляндии, Германии, США, Белоруссии и России. Каждая страна представляет по 2 пары участников. Какова вероятность того, что золотая медаль достанется России, серебряная – Белоруссии и бронзовая – Финляндии.
t) На 6 карточках написаны цифры 1, 3, 4, 6, 7, 9. Наугад берутся 2 карточки и составляется дробь. Какова вероятность того, что ее можно сократить на три?
u) В редакции газеты работают 7 корреспондентов. Редактор для беседы приглашает троих из них. Найти вероятность того, что корреспонденты будут вызваны в определенном порядке?
v) На прилавке магазина 60 одинаковых тетрадей в клетку. Из них 20 сделаны из бумаги второго сорта. Покупатель приобрел 15 тетрадей, из них 6 оказались второго сорта. Он решил купить ещё одну. Какова вероятность того, что эта тетрадь будет второго сорта?
w) В библиотеку института поступили 20 учебников по английскому языку. Из них три оказалось с браком. Для занятий в группе берут 7 учебников. Какова вероятность того, что среди них окажется один бракованный?
x) Секретный замок сейфа содержит шифр из пяти разных цифр. Оператор забыл первую цифру и набрал её наудачу. Какова вероятность того, что будет набрана верная цифра? Какова вероятность открыть сейф, если он забыл 3 первые цифры и набирает их наудачу?
y) В ремонтный цех поступило 12 осей для колесных пар. Из них три дефектные. Рабочий берет наудачу 2 оси. Найти вероятность того, что взята одна стандартная и одна дефектная ось.
z) Из букв слова «коммутатор», нанесенных на карточки, последовательно берется 5 букв и складываются в ряд. Какова вероятность того, что получится слово «мотор».
aa) У ребенка есть буквы нарезной азбуки и, о, у, з, н, к, м, м, м. Какова вероятность того, что раскладывая их подряд, он получит слово «коммунизм»?
bb) Из 50 взятых наудачу подшипников, оказались бракованными несколько штук. Частота появления брака 0,1. Сколько было бракованных подшипников?
cc) Квадрат с вершиной в начале координат и стороной 3 см пересекается с параболой 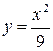 . Какова вероятность того, что наудачу брошенная точка попадет на участок квадрата, лежащий вне площади, ограниченной параболой?
. Какова вероятность того, что наудачу брошенная точка попадет на участок квадрата, лежащий вне площади, ограниченной параболой?
dd) Пять человек разного роста выстраиваются в одну линию. Найти вероятность того, что они выстроятся строго в убывающем порядке.
ee) В квадрат со стороной 3 см вписан круг радиуса 1 см, произвольно. Найти вероятность того, что точка брошенная в квадрат, окажется в круге.
ff) В окружность радиуса 5 см вписан квадрат. Наудачу брошена в круг точка, которая попадает в квадрат, вписанный в круг, с вероятностью 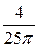 . Найти сторону квадрата.
. Найти сторону квадрата.
gg) Две параболы y = x2 и x = y2 пересекаются в точках (0,0) и (1,1) квадрата со стороной в 1 см, две стороны которого лежат на осях координат. Какова вероятность брошенной наудачу точке попасть на участок, ограниченной параболами?
hh) Подбрасываются две игральные кости белая и черная. Найти вероятность того, что на белой кости выпало не меньше 3 очков, а на черной – кратное трем.
ii) Два встречных поезда приходят в Красноярск с 10 до 11 часов. Стоянка каждого 15 минут. Каждый может прибыть с опозданием. Какова вероятность встречи поездов?
jj) Какова вероятность получить из слова «комбинация» слово, состоящее из двух гласных и трех согласных?
kk) Из пяти пронумерованных кубиков наудачу извлекают по одному три кубика. Найти вероятность того, что номера кубиков расположены в возрастающем порядке.
ll) На карточках написаны буквы э, л, е, р, т, о, з, в, о, к. Ребенок берет по одной и раскладывает их в ряд. Какова вероятность того, что получится слово «электровоз»?, слово «лектор»?
mm) Набирая номер телефона, абонент забыл две последние цифры, но помнит, что они разные. Абонент стал набирать их наудачу. Какова вероятность того, что абонент наберет нужный номер со второго захода?
nn) В ящике лежат 12 одинаковых тетрадей. Из них пять в линейку, остальные – в клетку. Взяты наудачу 3 тетради. Найти вероятность того, что из них хотя бы одна окажется в клетку.
oo) В коробке лежало несколько лампочек, причем две из них на 127 в, а остальные на 220в. Вероятность взять три лампы, из которых одна на 127 в, а две другие на 220в равна 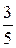 . Найти число лампочек в коробке.
. Найти число лампочек в коробке.
pp) Рыбак поймал 8 омулей и хариусов, примерно одинаковых по весу. Покупатель с вероятностью 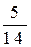 покупает у него 2 омуля. Сколько омулей и хариусов поймал рыбак?
покупает у него 2 омуля. Сколько омулей и хариусов поймал рыбак?
Задания
17. Изделие проходит проверку у трех контролеров. Вероятность того, что его забракует первый — 0,1, второй — 0,05, третий — 0,01. Найти вероятность того, что изделие будет забраковано.
18. Вероятность того, что в начале сентября выпадет снег — 0,05, что он выпадет в середине сентября — 0,1, что он выпадет в конце месяца — 0,2. Найти вероятность того, что в сентябре выпадет снег.
19. Вероятность студенту сдать экзамен по физике на «пять» равна 0,1, на «четыре» — 0,2, на «три» — 0,3, на «два» — 0,05. Какова вероятность студенту сдать экзамен на положительную оценку?
20. Американский бомбардировщик ведет прицельное бомбометание по объектам на территории Югославии. Причем, попадая в один из намеченных объектов, он поражает ещё два. Вероятность попадания в каждый из объектов соответственно 0,035; 0,03; 0,015. Найти вероятность того, что намеченные объекты не будут поражены?
21. Завод отправил электрочайники в количестве 100 штук в магазин. Из них 80 штук первого сорта, 15 штук — второго сорта и 5 штук — бракованная продукция. Какова вероятность того, что отобранный наудачу чайник оказался либо первого, либо второго сорта?
22. Ребенок перемешал семена яблок «Семеринка» и «Фуше». Какова вероятность посадить три семени одного сорта, если «Семеринки» было 8 штук, а «Фуше» — 6? Какова вероятность, что будут посажены семена разных сортов?
23. На сортировочную горку поступают товарные, почтовые, пассажирские и багажные вагоны с вероятностью соответственно 0,3; 0,2; 0,4 и 0,1. Какова вероятность того, что на сортировочную горку поступит какой либо вагон из товарных или почтовых или пассажирских?
24. В детский новогодний подарок положили 6 конфет «Ласточка»,4 конфеты «Белочка» и 5 конфет «Стратосфера». Ребенок берет три конфеты. Найти вероятность того, что среди них окажутся две одинаковые.
25. Предприниматель ожидает телеграфные извещения из трех городов: Москвы, Минска и Владивостока Вероятность получения телеграммы из Москвы — 0,5, из Минска — 0,3. Найти вероятность получения извещения из Владивостока.
26. Профком выделяет три путевки в дом отдыха студентам за хорошую успеваемость. Поощрения заслуживают пять студентов Вадим, Николай, Стас, Ирина и Ольга. Найти вероятность того, что поощрения путевками получат Вадим и Николай или Стас и Ирина или Николай, Ольга и Стас.
27. Подбрасываются одновременно три игральных кости. Какова вероятность того, что на всех трех выпадут цифры «5»?
28. На трех полках находится по десять книг. Из них на первой полке — 8 книг последнего года издания; на второй — 6; на третей — 4. Наудачу берут по одной книге с каждой полки. Какова вероятность того, что все три книги окажутся последнего года издания? Что книги не окажутся последнего года издания?
29. В трех коробках лежат карандаши по 40 штук в каждой. Красные — в первой коробке; синие — во второй; зеленые — в третей. В каждой коробке смешаны карандаши двух фабрик. Фабрики им. Кирова в первой коробке 20 штук; во второй —15; в третьей —18, остальные изготовлены на фабрике им. «Сакко и Ванцетти». Наудачу из каждой коробки взято по карандашу. Какова вероятность того, что из первой коробки взят карандаш фабрики им. Кирова, а из второй и третьей — карандаш, изготовленный на фабрике им. «Сакко и Ванцетти»?
30. В магазине по одинаковой цене продаются швейные изделия, изготовленные на двух швейных фабриках. 40 штук изготовлено Московской фабрикой, а 30 — Ивановской. Два покупателя, независимо друг от друга наудачу покупают по одному одинаковому изделию. Какова вероятность того, что оба купили изделия одной и той же фабрики?
31. Спортсмен в одной секции магазина покупает лыжные ботинки, а в другой — лыжи. Лыжных ботинок в магазине 10 пар, из них четыре нужного размера. Лыжных пар разных марок — 16, из них 7 пар марки «Енисей». Какова вероятность того, что спортсмен купит лыжи марки «Енисей» и лыжные ботинки нужного размера?
32. Два станка штампуют различные заготовки для изделия. Первый станок на 50 заготовок допускает 2% брака, второй — на 80 заготовок — 5% брака. Рабочий берет по одной заготовке с каждого станка. Какова вероятность того, что первая и вторая заготовки не бракованные?
33. Завхозу надо заменить в общежитии 4 электролампы. Из них две на 100 Вт и две на 60 Вт. В одной коробке лежат 20 ламп на 100 Вт, из них 5 штук не стандартные; в другой — 16 ламп на 60 Вт, из них 4 нестандартные.
a. Какова вероятность того, что завхоз возьмет по две стандартные лампы на 100 и на 60 Вт?
b. Какова вероятность того, что все взятые завхозом лампы окажутся нестандартными?
2. Схема состоит из трех последовательно соединенных блоков. Надежности блоков соответственно равны 0,9; 0,8; 0,6. Какова вероятность того, что схема не выйдет из строя?
3. На двух вазах яблоки трех сортов: «Фуше», «Семеринка», «Апорт». На каждой вазе по 12 яблок. Ребенок берет по одному с каждой вазы. Какова вероятность того, что оба яблока оказались сорта «Фуше», если на первой вазе их 5 штук, а на второй — 3. Какова вероятность, что с первой вазы он взял два яблока «Семеринки», а со второй одно сорта «Апорт», если всего он взял три яблока?
4. Два аквалангиста со дна моря достают затонувший предмет и опускаются под воду поочередно. Каждый предпринимает две попытки. Вероятность обнаружить предмет с одного захода для каждого аквалангиста равна 0,7. Какова вероятность того, что предмет будет найден?
5. Средства ПВО охраняют завод от воздушного налета. Противник совершил одну за другой 3 воздушные атаки. Вероятность поражения завода в одной атаке равна 0,3. Какова вероятность того, что завод
a. будет поражен противником?
b. не будет поражен противником.
6. Спортсмен–лыжник выполняет три прыжка с трамплина. Вероятность в каждом прыжке удачно приземлиться, равна 0,7. Найти вероятность того, что спортсмен–лыжник хотя бы один раз благополучно приземлился.
7. На соревнованиях разыгрывается золотая, серебряная и бронзовые медали. Вероятность получить золотую медаль — 0,7, серебряную — 0,8; бронзовую — 0,9. Найти вероятность того, что спортсмен получит хотя бы одну какую–либо медаль.
8. Спортсмен участвует в трех видах соревнований: лыжные гонки; прыжки с трамплина и стрельба из винтовки. Первое место он может занять в лыжных гонках с вероятностью 0,9; в прыжках с трамплина — с вероятностью 0,7; в стрельбе из винтовки — с вероятностью 0,8. Какова вероятность того, что он займет первое место во всех трех видах? Какова вероятность, что он займет первое место только в лыжных гонках и стрельбе из винтовки?
9. В коробке в произвольном порядке лежат двенадцать втулок, из них пять латунных. Рабочий последовательно достает 4 втулки. Какова вероятность того, что хотя бы одна из них латунная?
10. Проводится конкурс трех певцов. Вероятность получить высшую оценку для каждого одинакова и равна 0,7. Какова вероятность того, что только два певца получат высшую оценку? Какова вероятность того, что не более двух певцов получат высшую оценку?
11. В цехе работают четыре электромотора. Вероятность не выхода из строя каждого за время t равна 0,8. Найти вероятность того, что за это время
a. только один электромотор выйдет из строя;
b. по крайне мере два не выйдут из строя;
c. выйдут из строя не менее трех электромоторов.
12. В пяти ящиках находятся различные транзисторы. Сборщику радиотехнического узла необходим один определенный. В первом ящике он может находиться с вероятностью 0,3; во втором — с вероятностью 0,4; в третьем —0,2; в четвертом — 0,5; в пятом — 0,6. Найти вероятность того, что нужный транзистор содержится
a. не менее чем в трех ящиках;
b. во всех ящиках;
c. не содержится ни в одном ящике;
d. хотя бы один ящик содержит нужный транзистор.
13. Трех студентов независимо друг от друга попросили решить одну и ту же задачу. Первый может ее решить с вероятностью 0,8; второй — 0,6; третий — 0,7. Какова вероятность того, что
a. ни один студент не решил задачу;
b. хотя бы один студент решил ее;
c. решили два студента.
14. Студент добирается с занятий домой автобусом и троллейбусом. Вероятность того, что за время t к остановке подойдет нужный автобус, равна 0,9; а нужный троллейбус— 0,8. Какова вероятность того, что в течение времени t студент уедет домой?
15. В сеть включены последовательно два блока и сигнальная лампочка. Вероятность того, что за время t первый блок выйдет из строя равна 0,2; а для второго — 0,3. Найти вероятность того, что за время t сигнальная лампа погаснет.
16. Какова вероятность безотказной работы сети, если в схеме есть два дублирующих блока, причем первый не выходит из строя с вероятностью 0,6, а второй — с вероятностью 0,7.
17. Подбрасываются две кости белая и черная одновременно. Какова вероятность того, что на белой кости выпадет число очков меньшее трех, а на черной — число очков, кратное двум.
18. Игральная кость подбрасывается два раза поочередно. Найти вероятность того, что выпадет четное число очков при первом и втором бросании её.
19. Покупатель хочет приобрести спортивный костюм. Они продаются в трех магазинах. В первом он может купить его с вероятностью 0,9; во втором — 0,85; в третьем — 0,7. Какова вероятность того, что покупатель приобретет костюм?
20. Самолет – разведчик преодолевает две линии обороны противника. Вероятность того, что его могут сбить на первой линии равна 0,8; на второй — 0,7. Найти вероятность того, что самолет – разведчик не будет сбит.
21. Студент решил вечером пойти в театр. В кассе филармонии есть 22 билета. Из них 10 в драматический театр, а остальные в театр «Оперы и балета». Ему надо два билета в один театр. Какова вероятность того, что он купит билеты в театр.
22. Два спортсмена участвуют в розыгрыше серебряной медали. Вероятность того, что медаль будет получена первым из спортсменов равна 0,88. Найти вероятность получить медаль вторым спортсменом, если первый может ее получить с вероятностью 0,7.
23. Средства ПВО обнаружили вражеский самолет в воздушном пространстве страны. На поражение цели одна за другой посылаются три ракеты. Каждая может поразить самолет с вероятностью 0,8. Какова вероятность того, что самолет будет сбит?
24. Покупателю надо приобрести подарок для юбиляра. В одном магазине он может купить его с вероятностью 0,6; в другом — с вероятностью 0,8. Какова вероятность того, что покупатель сделает подарок юбиляру?
25. Рыбак закинул две удочки в разных местах реки. Вероятность того, что рыба клюнет на одну из них равна 0,8. Какова вероятность того, что рыба клюнет на первую удочку, если на вторую она клюет с вероятностью 0,5?
26. В коробке перемешаны пять красных кубиков, семь синих и четыре желтых. Ребенок достает наудачу по одному кубику. Какова вероятность того, что он сначала достанет красный, потом желтый, потом синий кубик?
27. В коробке перемешаны кубики с цифрами от 1 до 9, по одной цифре на каждом кубике. Ребенок достает три кубика и выстраивает их в ряд. Найти вероятность того, что у него получится число 143, если он доставая их поочередно
a. не возвращает кубики в коробку;
b. возвращает их обратно.
28. Два абитуриента сдают физику. Один выучил 20 вопросов из 30; а во второй — 10. Чтобы получить положительную оценку надо ответить на два вопроса из трех. Какова вероятность того, что оба получат положительную оценку?
29. Хозяйка предложила гостю к чаю три пирожка с капустой, три пирожка с морковкой, два с картошкой и два с повидлом. Пирожки произвольно положены на тарелке. Какова вероятность того, что гость взял сначала пирожок с капустой, потом с морковкой, а затем с повидлом? Какова вероятность того, что он сразу взял три пирожка с капустой, морковкой и повидлом себе на тарелку?
30. По жребию распределяются пять конвертов с двумя билетами в театр каждый. Причем в трех конвертах билеты на «Риголетто», а в двух на «Летучую мышь». Два студента наудачу поочередно берут конверты. Какова вероятность того, что второму студенту достанется конверт с билетами на «Летучую мышь», если первый студент вытащил конверт с билетами на этот же спектакль?
31. Продаются десять пар варежек. Из них шесть пар с узорами. Какова вероятность второму покупателю приобрести одну пару варежек с узорами, если первый взял две пары таких варежек?
32. Бомбардировщик производит бомбометание по целям на вражеской территории. Вероятность попадания бомбы в цель 3/4. Какова вероятность того, что цель будет взорвана, если 5% бомб могут не взорваться?
33. В составе поезда остались недоукомплектованными пассажирами два купейных вагона: старый и новый. В новом свободны 15 мест, из них 5 нижние, в старом — 20 мест, из них 8 нижние. Пассажир покупает билет в купейный вагон. Найти вероятность того, что
a. куплено нижнее место при условии, что вагон старый;
b. билет куплен в новый вагон, если известно, что место нижнее.
34. Проводник поезда дальнего следования раздает пассажирам постельное белье: комплекты голубого и белого цвета, сложенные в произвольном порядке. Всего голубых комплектов 12, белых —28. Вероятность брака для комплекта голубого цвета составляет 1/4, для комплекта белого цвета 3/14. Найти вероятность того, что пассажир получит комплект белого цвета и без брака?
35. Из четырех лыжников и трех конькобежцев отбираются в сборную завода четыре спортсмена. Какова вероятность того, что последовательно, один за другим будут выбраны два лыжника и два конькобежца? Какова вероятность того, что отбирая наудачу, будут выбраны сразу два лыжника и два конькобежца?
36. Цех обувной фабрики выпускает мужские ботинки. Часть изделий ОТК отправляет в брак, 70% не бракованных изделий оказываются изделиями первого сорта. Наудачу берут одно изделие. Оно оказывается с вероятностью 0,679 и не бракованным, и первого сорта. Какова вероятность брака, допускаемого фабрикой при выпуске изделий?
37. Из семи юношей и пяти девушек отбираются для сопровождения гостей три человека. Найти вероятность того, что при поочередном отборе будут выбраны двое юношей и одна девушка. Какова вероятность того, что наудачу будут назначены двое юношей (старший группы сопровождения и его помощник) и одна девушка?
38. В группе пятнадцать студентов. По одному к доске вызываются три студента. Какова вероятность того, что это будут Петров, Сидоров, Иванов? Какова вероятность Петрову, Сидорову, Иванову оказаться в числе трех студентов, вызванных наудачу к доске одновременно?
39. В воскресенье 16 студентов поехали отдыхать на речку. Из них четыре человека обгорели на солнце, а 6 человек были сильно покусаны комарами. Десять человек остались довольны всем. Какова вероятность одному студенту оказаться покусанным комарами и обгореть на солнце?
40. На конных состязаниях лошадь должна преодолеть шесть различных препятствий. Вероятность того, что она преодолеет все, равна 0,7. Вероятность того, что она преодолеет первое препятствие, равна 0,9. Какова вероятность преодолеть оставшиеся препятствия, если она преодолела первое?
41. Вероятность абитуриенту сдать первый вступительный экзамен 3/4. Если он его сдал, то получает право на второй экзамен по другому предмету. Вероятность того, что он сдает оба экзамена равна 1/2. Какова вероятность абитуриенту сдать второй экзамен?
Формула полной вероятности. Формула Бейеса
Пусть событие А наступает при условии, если имеет место одно из несовместных событий Н1, Н2,…,Нn, образующих полную группу. Их называют гипотезами.
Пусть известны или могут быть найдены вероятности этих гипотез, а также условные вероятности события А: Р(А/Н1) ; Р(А/Н2); ….. Р(А/Нn). Тогда вероятность события А равно сумме произведений вероятностей гипотез на соответствующие условные вероятности события А.
Р(А) = Р(Н1) Р(А/Н1)+Р(Н2) Р(А/Н2) + … + Р(А/Нn)
То есть 
Это и есть формула полной вероятности.
Если же, в результате испытания, событие А уже появилось, то можно найти как изменятся при этом вероятности гипотез по формуле Бейеса.
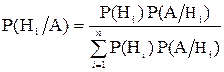
Пример 16. Три станка штампуют детали, I-ый – 300 шт. за смену; II - ой – 350 шт., а III-ий – 400 шт. Причем нестандартными оказываются на I-ом станке- 20 штук, на II-ом - 15; на III-м – 22шт. Детали поступают на общий конвейер. Рабочий берет на удачу одну деталь. Какова вероятность того, что рабочий взял стандартную деталь? Какова вероятность того, что эта деталь изготовлена на I-ом станке?
Решение . Событие А – рабочим взята стандартная деталь.
Выдвигаем гипотезы:
Н1 – стандартная деталь изготовлена Iм станком.
Н2 – деталь изготовлена II м станком.
Н3 - деталь изготовлена IIIм станком.
Так как станки производят разное количество деталей, то вероятность взятой детали принадлежать разным станкам не одинакова.
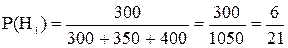 – вероятность того, что деталь изготовлена I-ым станком.
– вероятность того, что деталь изготовлена I-ым станком.
Аналогично для II-го и III-го станка:
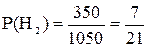 ;
; 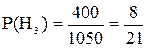
Так как, событие, что взятая деталь принадлежит к изделиям какого-то из 3-х станков, относится к полной группе событий, то 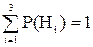 , т.е.
, т.е. 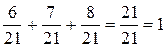
Найдем вероятность того, что взятая стандартная деталь изготовлена I-ым станком
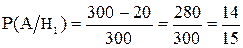
Аналогично для II-го и III-го станка
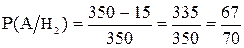
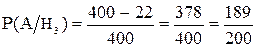
Но стандартная деталь, взятая рабочим, может быть произведена или на I-ом или на II-ом или на III-м станке.
Тогда, полная вероятность для взятой детали быть стандартной, равна
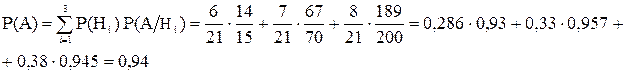
Зная, что взята стандартная деталь, ответим на 2-ой вопрос: с какой вероятностью она может быть произведена 1-м станком?
То есть мы должны найти вероятность 1-ой гипотезы при уже свершившемся событии А. Воспользуемся формулой Бейеса
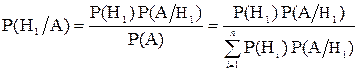
Формально эта формула означает отношение возможности стандартной детали быть изготовленной I-м станком ко всем возможностям детали оказаться стандартной.
Формализуя подобные жизненные ситуации, рассмотрим задачу о шарах.
Пример17. В 3-х одинаковых урнах находятся шары. В I-ой 20 белых и 10 синих; во II-ой 15 белых и 5 синих; в III-ей 10 белых и 10 синих. Из какой-то урны вынимается наудачу один шар. Какова вероятность, что он – синий. Какова вероятность того, что вынутый синий шар взят из 2-ой урны?
Решение . Событие А - вынут синий шар.
Выдвигаем гипотезы:
Н1 – синий шар вынут из I-ой урны
Н2 - синий шар вынут из II-ой урны
Н3 - синий шар вынут из III-ой урны
Так как шар может быть взят из любой урны, то гипотезы равновероятны. Следовательно
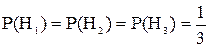 ;
; 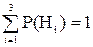
Вероятность того, что шар взят из I-ой урны
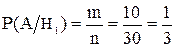 , где m – число случаев, благоприятствующих появлению синего шара, n – число всех возможных случаев вынуть шар из урны.
, где m – число случаев, благоприятствующих появлению синего шара, n – число всех возможных случаев вынуть шар из урны.
Аналогично для II и III-ей урны:
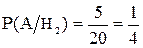 ;
; 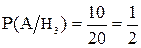
Тогда полная вероятность вынуть синий шар, будет
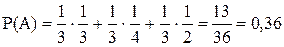
Пусть известно, что вынут синий шар (событие А произошло) тогда вероятность синему шару быть взятым из 2-ой урны по формуле Бейеса будет

Рассмотрим ту же задачу, но зададимся другой целью: какова вероятность вынуть одновременно 2 синих шара?
Решение . Событие А – вынуто два синих шара.
Выдвигаем гипотезы
Н1 – оба шара взяты из 1-ой урны
Н2 – оба шара взяты из 2-ой урны
Н3 - оба шара взяты из 3-ей урны
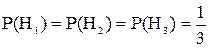
Найдем вероятность наступления события А при первой гипотезе
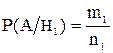 , где
, где 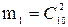 ;
; 
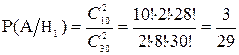
Аналогично
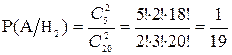 ;
; 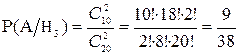
Тогда полная вероятность события А будет:
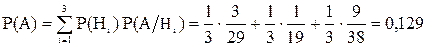
Пример 18. В урне 20 шаров. Из них 14 белых 7 синих. Из 14 белых шаров 4 штрихованные, а из 7 синих – 3 штрихованных. Наудачу одновременно вынимают 2 шара. Найти вероятность того, что они штрихованные.
Решение. Событие А – взяты 2 штрихованных шара
Выдвигаем гипотезы:
Н1 - оба шара белые;
Н2 – оба шара синие;
Н3 – 1 белый, 1 синий.
Найдем вероятности гипотез:
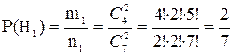
Аналогично для 2-ой и 3-ей гипотезы:
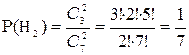 ;
; 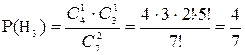
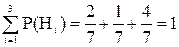
Событие А/Н1 - оба шара штрихованные, при условии, что они белые. Вероятность взять одни шар штрихованный при условии, что он белый, 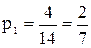 ; а при условии, что он синий
; а при условии, что он синий 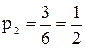 .
.
Но из урны берут 2 шара одновременно. Тогда вероятность взять 2 шара штрихованных, при условии, что они белые, будет
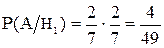
Аналогично для остальных гипотез
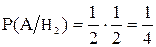 ;
; 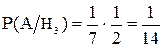
Тогда полная вероятность взять 2 штрихованных шара любой окраски
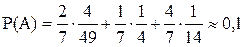
Задания
1. В двух ящиках стола лежат одинаковые тетради в клетку и в линейку. В 1-ом 20 в клетку и 15 в линейку; во 2-ом – 14 в клетку и 28 в линейку. Берется наугад одна тетрадь. Какова вероятность, что она в клетку?
2. Два цеха А и В производят одинаковую радиоаппаратуру, которая поступает на продажу. Цех В производит втрое больше изделий, чем цех А. Количество бракованных изделий в цехе А – 1%, а в цехе В – 4%. Заказчику поступило изделие. Найти вероятность того, что оно оказалось бракованным?
3. Три станка механического цеха штампуют заготовки для болтов, причем первый штампует в 2 раза больше, чем второй, а 3-ий – в 3 раза больше, чем второй. Первый станок дает 4% брака, второй – 3%, третий – 5%. Детали поступают на общий конвейер. Рабочий наудачу берет одну заготовку. Найти вероятность того, что она не бракованная.
4. В библиотеке на 2-х книжных полках стоят учебники и задачники по математике одинакового формата. На 1ой полке 10 задачников и 8 учебников, на 2ой – 6 задачников и 9 учебников. Библиотекарь случайным образом переложил одну книгу с 1ой полки на 2ую. Какова вероятность того, что читатель возьмет со 2-ой полки учебник по математике?
5. Летчик делает вылет на бомбометание по 3м складам боеприпасов. Причем попадание в один из них приводит к взрыву двух других. Вероятность взрыва 1-го склада – 0,6; 2-го – 0,7; 3-го – 0,65. Найти вероятность уничтожения складов.
6. В мехмастерских 3 станка разрезают листовой металл по одинаковому шаблону. Заготовки поступают на общий конвейер. Первый станок производит 300 заготовок в смену, второй – 350, а 3-ий 400. Брак 1-го станка 2%, второго – 3%, а третьего в 2 раза больше, чем 1-го. Найти вероятность того, что наудачу взятая деталь не бракованная.
7. Студенту надо купить 2 билета на спектакль в театр. В городе есть 3 кассы, где он может их купить. Вероятность обращения в любую кассу зависит от ее местоположения и составляет соответственно 0,3; 0,5; 0,2. Студент может купить билет в 1ой кассе с вероятностью 0,6; во 2ой – 0,8; в 3-ей – 0,7; т.к. часть билетов может оказаться распроданной. Какова вероятность того, что студент купит 2 билета?
8. На городские соревнования отбираются 2 спортсмена из заводской команды лыжников и конькобежцев. Лыжников в команде 10 человек, конькобежцев – 6. Вероятность выиграть кубок лыжнику – 0,8; конькобежцу – 0,7. Найти вероятность того, что будут выиграны 2 кубка.
9. Пассажир покупает 2 билета до нужного пункта в день отправления поезда. Он может добраться до места поездами двух назначений, причем на поезд одного назначения в кассе осталось 10 билетов, а на поезд другого назначения 8 билетов. Вероятность того, что он возьмет билет на поезд одного назначения 0,9; а на поезд другого назначения – 0,8 (возможности пассажира). Найти вероятность того, что пассажир купит 2 билета.
10. Институту необходимо приобрести 3 одинаковых прибора. В магазине есть нужные приборы 2х сортов: 10 приборов I сорта и 8 – IIго. Вероятность быть исправным прибору I сорта – 0,9, а второго – 0,7. Найти вероятность того, что наудачу купленные 3 прибора окажутся исправным.
11. В магазин поступили 2 партии одинаковых изделий разного цвета. В 1ой 10 изделий коричневого цвета и 6 бежевых. Во 2ой – 8 коричневых и 12 бежевых. Продавец случайно переложил одно изделие во 2ую партию. Какова вероятность того, что покупатель из 2ой партии купит 2 изделия бежевого цвета.
12. Два предприятия выпускают электробытовые приборы. Первое выпускает 20 штук за 1 час. второе – 15 штук. Из них второго сорта 20% и 10% соответственно. Продукция поступает на склад. Наудачу берут 2 электробытовых прибора. Найти вероятность того, что они оба 1-го сорта.
13. На диспетчерский пункт поступают сведения о количестве отправленных за день пассажирских и товарных поездов с 3-х подразделений дороги (Ачинского – А; Канского – В; Красноярского – С). Из А отправлено в 2 раза больше пассажирских, чем товарных поездов, из С – товарных в 3 раза больше, чем пассажирских, а из В – и тех и других одинаково. В диспетчерской на дисплей выводится произвольный номер пассажирского состава. Найти вероятность того, что он относится к подразделению А.
14. Два предприятия выпускают видеокассеты. Первое – 500 шт. за смену, второе – 700. Из них некачественных соответственно 2 и 3 шт. Кассеты направляются на склад. Наудачу берется одна кассета. Она оказалась некачественной. Найти вероятность того, что ее изготовило 2ое предприятие.
15. Завод готовит к выпуску 3 пассажирских состава. В первом 10 плацкартных и 6 купейных вагонов. Во втором 8 плацкартных и 7 купейных; в третьем 5 плацкартных и 9 купейных вагонов. Для контроля готовности выбирают из наудачу выбранного состава один вагон. Он оказался купейным. Найти вероятность того, что это вагон второго состава.
16. В магазин поступила 3 партии коробок с электролампами. В первой партии 3 коробки. В каждой по 30 ламп на 220 В и 20 ламп на 127. Во второй партии 2 коробки по 40 ламп на 220В и 10 ламп на 127 В в каждой. В третьей – 4 коробки по 10 ламп на 220В и 40 ламп на 127 в каждой. Из наудачу выбранной коробки вынимается лампа. Она оказалась на 220В. Найти вероятность того, что она взята из коробки 3ей партии.
17. При массовом пошиве костюмов число изделий I-го сорта составляет 96%, остальные зачисляются II-м сортом. Перед поставкой в магазин изделия проходят еще один контроль. При этом из изделий I-го сорта пропускается только 98%, а из изделий II-го сорта переводится в I-ый 3%. Какова вероятность изделию I-го сорта выдержать проверку?
18. В день военно-воздушного флота проводятся показательные выступления парашютистов. Надо приземлиться в заранее намеченный квадрат с высоты 1км. Выбирается любой из 3-х подготовленных парашютистов, причем 1ый может приземлиться с вероятностью 0,8; второй – 0,95; третий – с вероятностью – 0,9. Выбранный наудачу парашютист приземлился точно в квадрат. Найти вероятность того, что это был 3ий парашютист.
19. Студенту надо купить книгу по математике. Ее можно купить в 3-х магазинах. Первый находится на расстоянии 600м, второй – 700м, третий – 500м от покупателя. Но в первом магазине он может купить книгу с вероятностью 0,8; во втором – 0,7; в третьем – с вероятностью 0,5. Найти вероятность того, что студент купит книгу в третьем магазине.
20. Сессия. Группа студентов из 12 человек сдает экзамен. Надо было подготовить 26 вопросов. 5 студентов подготовились отлично. Они знают все 26 вопросов. 4 студента подготовились хорошо. Они знают 20 вопросов из26. И 3 студента подготовились плохо. Они знают только 6 вопросов. Наугад вызванный студент ответил на 3 заданных вопроса и получил «Отлично». Найти вероятность того, что это был плохо подготовленный студент.
21. Спортсмены-авиаторы участвуют в показательных выступлениях в день авиации. Всего 12 человек. Из них 4 мастера спорта, 5 кандидатов в мастера и 3 спортсмена, подающих надежды. Для показательных выступлений наудачу выбирается один. Он выполняет на отлично 3 предложенные фигуры высшего пилотажа из 15. Причем мастер спорта может отлично выполнить все 15 фигур, кандидат в мастера – 13, а спортсмен, подающий надежды - 5. Найти вероятность того, что был выбран спортсмен, подающий надежды.
22. Летчику предлагается взорвать 2 склада с боеприпасами №1и №2. Причем, при поражении одного, взрывается и второй. У летчика боезапас – 3 бомбы и он располагает резервом времени на 3 захода на цель. Вероятность поражения цели №1 при одном заходе р1 =0,6, а цели №2 – р2=0,7. Найти вероятность того, что задание будет выполнено.
23. В боевых учениях военно-морских сил принимает участие подводная флотилия. Подлодка потонет, если будут пробиты отсеки №1 и №2. Вероятность пробоя отсека №1 – р1= 0,3; а отсека №2 – р2=0,2. Бой длился t мин. В результате подлодка вышла из строя. Найти вероятность того, что был пробит отсек №1, а №2 – нет.
24. Латунные и бронзовые втулки находятся в 2х ящиках. В первом 16 латунных и 18 бронзовых. Во втором – 20 латунных и 30 бронзовых. Из произвольного ящика наудачу берется одна втулка. Она оказалась латунной. Найти вероятность того, что следующая вынутая втулка будет тоже латунной.
Формула Бернулли
Пусть проводится n независимых испытаний. В каждом из них вероятность появления события А равна р. Найти вероятность того, что среди n независимых испытаний событие А появится ровно k раз (Рn (k)).
Вероятность одноразовому событию А произойти k раз и не произойти (n – k) раз равна pk ×qn-k , где q=1–p
Число таких событий задается числом способов наступления события А, то есть равно числу сочетаний из n испытаний по k ( 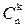 ).
).
Тогда, искомая вероятность равна
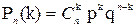
Это и есть формула Бернулли.
Пример 19. Найти вероятность того, что в 6 независимых испытаниях событие А появится 2 раза, если в каждом испытании вероятность его появления равна р=0,3.
Решение. n = 6; k=2; р=0,3; q=1–р=0,7.
Одно сложное событие состоит в том, что событие А наступит 2 раза и не наступит 4 раза. Его вероятность равна
0,32×(1–0,3)4=0,32×0,74
Число таких случаев 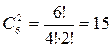
Тогда, вероятность того, что событие А наступит 2 раза в 6 испытаниях равна
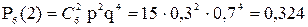
Пример 20. Стрелок стреляет по мишени 8 раз. Вероятность попадания при каждом выстреле 3/4. Найти вероятность того, что он попадет в мишень не менее 2х раз.
Решение. n = 8; k³2; р= 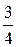 ; q=1–р=
; q=1–р= 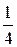 .
.
Событие А – стрелок попал в мишень не менее 2-х раз. Значит он попал в мишень или 2, или 3, … или 8 раз. Тогда, по теореме сложения вероятностей несовместных событий
Р8(k³2)= Р8(2)+ Р8(3)+ Р8(4)+…+ Р8(8)
Но подсчитывать все вероятности – процесс трудоемкий. Проще подсчитать вероятность противоположного события
Р8(k<2)= Р8(k=0)+ Р8(k=1)
Тогда Р8(k³2)= 1– Р8(k<2)
т.е.
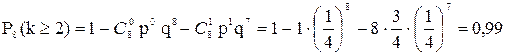
Если число испытаний, (n) велико, то вычисления по формуле Бернулли громоздки. В этом случае применяют приближенные формулы Муавра-Лапласа или Пуассона.

Пример 21. Найти вероятность того, что при 40 выстрелах стрелок поразит мишень 30 раз. Вероятность поражения стрелком мишени при одном выстреле р=0,8.
Решение. n = 40; k=30; р=0,8; q=1–р=0,2
Так как вычисления по формуле Бернулли громоздки, воспользуемся формулой Муавра-Лапласа.
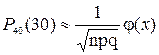
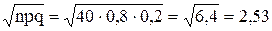
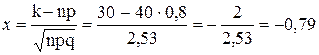
В таблице значений четной функции 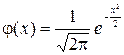 находим j(–0,79)= j(0,79)=0,2920
находим j(–0,79)= j(0,79)=0,2920
Тогда 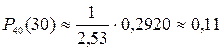
Пример 22. На железнодорожном вокзале кассир обслуживает в течение недели 600 пассажиров. Вероятность ошибки в оформлении билета равна 0,003. Какова вероятность того, что будет оформлено неверно а) 2 билета? б) не больше 2-х билетов.
Решение . n = 600; р=0,003; k1=2; k2£2;
Т.к. np=l=1,8<10, воспользуемся формулой Пуассона для вычисления вероятности
а) 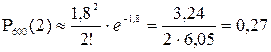
б) 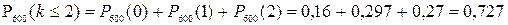
Когда требуется вычислить вероятность наступления события А не менее k1 раз и не более k2 раз можно воспользоваться точной формулой
P(k1 £ n £ k2)=Pn(k1)+Pn(k1+1)+…+Pn(k2)
или, во избежание громоздких вычислений (при k1>10), приближенной формулой Лапласа (интегральной теоремой Лапласа)
P(k1 £ n £ k2)=Ф(x//)–Ф(x/), где
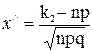 ;
; 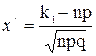
где 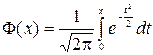 – нечетная ( табулированная)
– нечетная ( табулированная)
Пример 23. Вероятность поражения мишени стрелком при одном выстреле 0,6. Найти вероятность того, что из 50 выстрелов мишень будет поражена не менее 30 и не более 40 раз.
Решение . n=50; k1=30; k2= 40; p=0,6; q=1–0,6=0,4
Задания
20. 10 мощных ламп освещают съемочную площадку в Останкино. Съемка телесюжета идет 5 часов. Вероятность одной лампы выйти из строя за это время 0,4. Какова вероятность того, что 4 лампы из 20 за время съемки выйдут из строя?
21. Студент с вероятностью 0,8 решает задачу. Какова вероятность решить ему 3 задачи из 5?
22. На склад поступили 6 приборов, из них 4 – II-го сорта. Какова вероятность взять потребителю наудачу 2 прибора II-го сорта?
23. Производится 5 подбрасываний игральной кости. Найти вероятность того, что цифра «6» появится хотя бы 2 раза.
24. Вероятность поражения стрелком мишени р=0,6 при одном выстреле. Найти вероятность того, что из 4х выстрелов стрелок поразит мишень не менее 3х раз.
25. К бензоколонке на заправку в течение дня подходит 100 автомашин. Из них 40 грузовых. За время t заправилось 10 автомашин. Какова вероятность того, что среди них окажутся две грузовые.
26. За смену станок производит 100 деталей. Из них 10 бракованные. Наудачу берут 7 деталей. Найти вероятность того, что хотя бы 3 из них будут бракованные.
27. На праздничном вечере разыгрывается 100 лотерейных билетов, из которых 60 выигрышные. Найти вероятность того, что у владельца 5 лотерейных билетов выигрышными окажутся не менее 3-х билетов.
28. Вероятность студенту взять 1 билет в театр «Оперы и балета» 0,5, а в драматический – 0,6. Студент хочет взять на вечер 2 билета. В театре «Оперы и балета» в кассе осталось 8 билетов, а в драматическом – 6. Какова вероятность студенту взять два билета в какой-либо театр?
29. Летчик поражает летящую учебную цель с вероятностью 0,9. Он делает 5 выстрелов. С какой вероятностью он поразит мишень хотя бы 3 раза из 5.
30. Два парашютиста выполняют прыжки с самолета . Вероятность приземлиться в обозначенное место для 1-го парашютиста – 0,8, для 2-го – 0,7. Первый совершает 5 прыжков, второй – 4. Какова вероятность 1му и 2му парашютисту приземлиться в обозначенное место не менее 2-х раз?
31. Цех завода выпускает за время t 200 ламп дневного света. Из них бракованными оказываются 20 штук. На повторный контроль отбирается 10 ламп. Какова вероятность того, что среди них окажется менее 2-х бракованных?
32. Подбрасываются 3 игральные кости 3 раза. Какова вероятность того, что цифра «6» выпадет на 1ой кости 2 раза; на 2ой – не менее 2-х раз и на 3ей – 1 раз?
33. Студент получит стипендию, если он сдаст все 5 экзаменов и из них на «отлично» не менее 3-х. Вероятность студенту сдать на «отлично» один экзамен равна 0,7. Какова вероятность того, что студент получит стипендию?
34. Предприятие начнет выпуск продукции, если оно поучит станки 2х видов. Причем станков I-го вида не менее 3х из 5, а II-го вида хотя бы 2 из 6 планируемых. Вероятность поставки станка I-го вида – 0,7, а II-го – 0,6. Какова вероятность предприятию начать работать?
35. Два стрелка стреляют по 2м различным целям и делают по 5 выстрелов. Вероятность поразить цель при одном выстреле для 1го стрелка – 0,6, для второго – 0,7. Найти вероятность того, что первый попадет в цель не больше 3х раз, а второй – не меньше 3х раз.
36. На склад доставили две упаковки с приборами в количестве 5 и 6 штук в каждой. Вероятность повреждения прибора в пути для первой упаковки 0,4, для второй – 0,3. Найти вероятность того, что при транспортировке оказались поврежденными 3 прибора 1ой упаковки и два второй.
37. В магазине продается живая рыба: форель и карпы в количестве 20 штук, среди которых карпов 6. Какова вероятность, что продавец выловит наудачу а) сразу 2х карпов; б) 2х карпов по очереди?
38. Группа студентов получает приз, если выйдет на первое место хотя бы по 2м из 3х показателей по успеваемости, по посещаемости занятий и по художественной самодеятельности. В группе по итогам сессии на положительные оценки из 25 человек сдало 20. По итогам посещаемости за семестр вероятность получить 1ое место составляет 0,7, а по художественной самодеятельности – 0,8. Какова вероятность выйти группе на 1ое место?
39. Система состоит из двух агрегатов, задействованных последовательно. Первый содержит 4 одинаковых, независимо работающих друг от друга блока, второй – 5. Вероятность выйти из строя одному блоку 1го агрегата 0,3, а для блока 2го агрегата – 0,2. в течении года система отключается, если какой либо агрегат выходит из строя. Первый агрегат отключается при выходе из строя одного блока. Второй – при выходе из строя двух блоков. Какова вероятность , что система в течение года отключится?
40. Игральный кубик подбрасывается 300 раз. Найти вероятность того, что цифра «5» появится 40 раз.
41. Вероятность появления события А в каждом из независимых испытаний равна 0,3. Найти вероятность того, что событие А наступает 80 раз в 300 испытаниях.
42. Станок штампует в смену 400 заготовок для болтов. Вероятность появления брака для каждого болта 0,2. Найти вероятность того, что брак появится у 50 болтов.
43. Вероятность появления события А в каждом из 2100 независимых испытаний равна 0,7. Вероятность того, что событие появится k раз равна 0,0189. Найти число k.
44. Партию телевизоров в 1000 штук завод доставляет на склад магазина. Вероятность повреждения в пути одного телевизора 0,001. Найти вероятность того, что в пути повреждено 3 телевизора.
45. Радиоэлектронная система содержит 3000 резисторов. Вероятность отказа каждого из них 0,0004. Какова вероятность отказа системы, если она выходит из строя при отказе хотя бы 2х элементов.
46. Два зенитных орудия стреляют по одной цели. Первое попадает в цель с вероятностью 0,6, а второе – с вероятностью 0,5. Сколько будет сделано залпов, при которых оба орудия попадут в цель, если общее число залпов равно 10?
47. Обувной цех в течение смены выпускает 300 пар обуви. Вероятность брака одной пары р=0,01. Какова вероятность того, что будет забраковано а) 3 пары обуви? б) не более 3х пар обуви?
48. Трикотажная фабрика выпускает перчатки, которые выборочно проходят ОТК. Вероятность одной паре перчаток не пройти ОТК равна 0,3. Какова вероятность того, что из 300 отобранных наудачу пар перчаток от 60 до 100 не пройдут ОТК?
49. Вероятность того, что на железнодорожном участке пути АВ при прохождении состава поезда произойдет авария равна 0,01. Найти вероятность того, что из 1000 составов , проходящих по этому участку за неделю безаварийно пройдут не больше 900 составов.
50. Вероятность появления события А в каждом из 24 независимых испытаний равна 0,6 . Найти вероятность того, что событие появится: А) не более 12 раз; б) менее 12 раз.
51. Выпущено120 лотерейных билетов. Из них 40 выигрышных. Сколько надо купить билетов, чтобы наивероятнейшее число выигравших билетов равнялось 5.
52. 100 штук футболок, выпущенных цехом, проходят ОТК. Вероятность для футболки быть забракованной равна 0,1. Найти наивероятнейшее число футболок, наудачу отобранных для ОТК, которые окажутся забракованными.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайная величина – отвлеченное выражение случайного события. Это величина, которая в результате опыта примет одно возможное, наперед неизвестное значение, зависящее от случайных причин. Случайную величину обозначают X, Y, Z, а ее количественные значения xi, yi, zi (i = 1,…,n).
 Если, например, x1, x2 …, xn образуют дискретный ряд чисел, то X называется дискретной случайной величиной (ДCВ). Если же количественные значения заполняют промежуток (а,в), то X называется непрерывной случайной величиной (НСВ). Каждому значению случайной величины ставится в соответствие определенная вероятность его появления в опыте. Распределение вероятностей описывается законом. Для ДСВ Х это – ряд распределения, т.е. таблица, где каждому xi соответствует определенное значение вероятности его появления pi, причем xi < xi+1; и
Если, например, x1, x2 …, xn образуют дискретный ряд чисел, то X называется дискретной случайной величиной (ДCВ). Если же количественные значения заполняют промежуток (а,в), то X называется непрерывной случайной величиной (НСВ). Каждому значению случайной величины ставится в соответствие определенная вероятность его появления в опыте. Распределение вероятностей описывается законом. Для ДСВ Х это – ряд распределения, т.е. таблица, где каждому xi соответствует определенное значение вероятности его появления pi, причем xi < xi+1; и 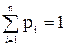 . Графически это – многоугольник распределения.
. Графически это – многоугольник распределения.
Для непрерывной случайной величины характеристикой вероятности появления xi в интервале (x; x+Dx) является плотность вероятности f(x) (аналогично распределению массы вдоль Ох в механике, если она распределена по какому-то закону). Это неотрицательная функция и 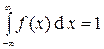 .
.
Функция плотности позволяет вычислить вероятность попадания НСВ Х в интервал (а,b), т.е.
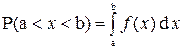
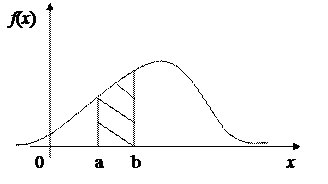 Графически функция плотности напоминает «колокольчик», а вероятность попадания в заданный интервал есть площадь, ограниченная этой кривой на (a,b).
Графически функция плотности напоминает «колокольчик», а вероятность попадания в заданный интервал есть площадь, ограниченная этой кривой на (a,b).
Зная ряд распределения или функцию плотности вероятности, можно построить соответствующую функцию распределения F(x). Ее еще называют интегральной функцией распределения, а f(x) - дифференциальной функцией плотности.
Задания
1. a) Пассажир делает три попытки купить билет на поезд, причем вероятность того, что он купит билет с одной попытки равна 0,7. Составить закон распределения числа попыток купить билет.
P(1£ X £2)
 b)
b)
| a=1; b=2 |
2. a) Проводится 4 независимых испытания рессоры для вагона. Вероятность благополучно пройти одно испытание равна 0,8. Составить закон распределения испытаний, которые рессора пройдет благополучно.
P (2<X<4)
b)
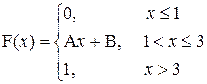
| a=1,5; b=2 |
3. a) Управление вагоно-ремонтного завода выпустило 100 новогодних лотерейных билетов для работников завода достоинством 10 руб. —50 шт., 50 руб. —20 шт., 70 руб. —10 шт., 100 руб. — 1шт.
Остальные билеты невыигрышные. Составить закон распределения стоимости выигрыша владельцем одного лотерейного билета.
P(50< X £100)
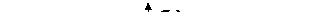 b)
b)
| a= –2,5; b= –1 |
4. a)
| x | –2 | –1 | 0 | 1 | 2 |
| p | 0,1 | 0,2 | 0,3 | p | 0,15 |
P(–2< X £ 0)
b)
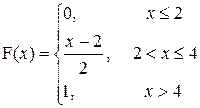
| a =3; b=2,5 |
5. а) В магазин поступили учебники по 3м дисциплинам математике, физике, теории вероятностей. Студент намерен приобрести 3 разных учебника. Вероятность купить любой из них равна 0,6. Пусть Х – число различных учебников, купленных студентом. Составить закон распределения чисел купленных книг.
Р(0 £ Х < 2)
 b)
b)
| a= –2; b= –1 |
6. a) В математической олимпиаде предлагается решить 5 задач. Студент решает любую задачу с вероятностью 0,8. Составить закон распределения числа решенных задач.
P (3£ X £5)
b)
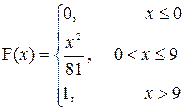
| a=3; b=5 |
7. a) В цехе завода производят оси вагонных колес. В партии из 6 пронумерованных осей 1 бракованная. Брак выявляют, проверяя одну ось за другой, выбирая их наудачу. Найти закон распределения номера выбранной для проверки оси, включая бракованную.
P (1<X<3)
 b)
b)
| a=2; b=¥ |
8. a) Товарная станция имеет контейнеры различного тоннажа для перевозки груза: 1,5 т, 3 т, 5 т и 7 т. Она выделяет заказчику один контейнер. Составить ряд распределения тоннажа выделенного заказчику контейнера.
P (1<X<3)
b)
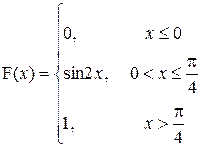
|
a=0; b= 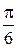
|
9. a) Деталь проходит три этапа контроля. Вероятность нахождения дефекта на первом этапе p1=0,2; на втором – p2=0,3; на третьем – p3=0,1. X – число случаев нахождения дефекта. Составить закон распределения случайной величины X.
P (0≤X<2)
 b)
b)
| a=1,5; b=3 |
10. a) Пассажиру надо купить в железнодорожной кассе 3 билета на поезда трех разных назначений. Вероятность купить билет на поезд 1-ого назначения p1=0,8; на поезд 2-ого назначения p2=0,7; на поезд 3-его назначения p3=0,6. Пусть X – число случаев приобретения пассажиром билетов. Найти закон распределения случайной величины X.
P (1≤X<3)
b)
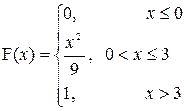
| a=1; b=4 |
11. a) На пути из города A в город B поезд проходит 5 светофоров. Каждый из них разрешает проезд или запрещает. Пусть X – число светофоров, пройденных поездом до первой остановки. Найти закон распределения случайной величины X.
P (X>2)
b)

| a=0; b=1,8 |
12. a) Вагоно-ремонтный завод выпускает в месяц 60% пассажирских вагонов и 40% – товарных. Наудачу берут для контроля качества ремонта 5 вагонов. Пусть X – число пассажирских вагонов. Составить закон распределения случайной величины X.
P (2<X≤ 5)
b)
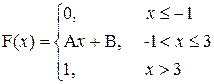
| a = 0; b=2 |
13. a) 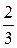 всех сотрудников заводоуправления имеет высшее образование и
всех сотрудников заводоуправления имеет высшее образование и 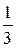 средне-техническое. Отбираются наудачу 5 человек. Составить закон распределения числа сотрудников с высшим образованием.
средне-техническое. Отбираются наудачу 5 человек. Составить закон распределения числа сотрудников с высшим образованием.
P(2<X<3)
b)
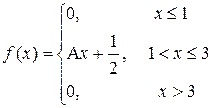
| a =0,5; b=2 |
14. a) На склад поступило 600 м провода, причем высоковольтного из них 100 м диаметром 10 мм; 150 м диаметром 15 мм; 200 м диаметром 25 мм; 50 м диаметром 20 мм; 40 м диаметром 30 мм.
Остальной невысоковольтный. Потребитель заказал высоковольтный провод. Составить закон распределения высоковольтного провода по размеру его диаметра.
P (10≤X≤20)
b)
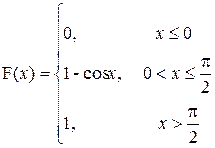
|
a= 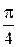 ; b= ; b= 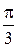
|
15. a) Поезд следует из города А в город В через пункты С и D. Вероятность опоздания на участке АС составляет p1=0,3; на участке CD – p2=0,4; на участке DB – p3=0,35. Пусть X – число участков, на которых может произойти опоздание поезда. Найти закон распределения случайной величины X.
P (0<X≤3)
b)
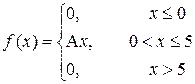
| a =2; b=6 |
16. a) Для ремонта локомотива требуются три детали различного назначения. В цехе три автомата производят эти детали в стандартном качестве с вероятностями 0,9; 0,8; 0,7. Пусть X – количество отобранных стандартных деталей. Найти закон распределения случайной величины X.
P (0≤X<2)
b)
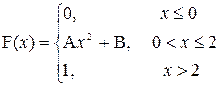
| a=0; b=1 |
17. a)
| x | –2 | –1 | 0 | 1 | 2 |
| p | 0,1 | 0,2 | p | 0,25 | 0,15 |
P (–1≤X<1)
b)
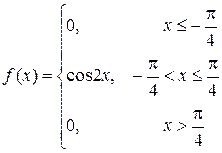
|
a=0; b= 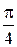
|
34. a)
| x | 1 | 1,5 | 2 | 4 | 5 |
| p | 0,1 | 0,05 | 0,1 | 0,35 | p |
P (1,5≤X≤5)
b)
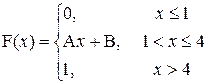
| a=2; b=3 |
19. a) На конкурс предложено 5 проектов прокладки железнодорожной магистрали, из которых может быть принят только один. Проекты по одному проходят предварительное обсуждение. Проект, не прошедший его, из конкурса исключается. Пусть X – число проектов, прошедших предварительное обсуждение. Составить закон распределения случайной величины X.
P (1,5≤X≤3,5)
 b)
b)
| a=0; b=2,5 |
a)
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0,03 | p | 0,3 | 0,35 | 0,1 |
P (1≤X≤3)
b)
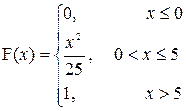
| a=2; b=4 |
21. a) На товарную станцию прибыло 3 партии одинаковых контейнеров по 12 штук в каждой, причем в первой партии 3 нестандартных, во второй – 7, в третьей – 2. Из каждой партии отбираются по одному контейнеру. Составить закон распределения отбора стандартных контейнеров.
P (0,5≤X<2,5)
 b)
b)
| a=1,5; b=2,5 |
22. a)
| x | 1 | 3 | 5 | 7 | 9 |
| p | 0,2 | 0,1 | 0,1 | 0,4 | 0,3 |
P (1≤X≤5)
b)
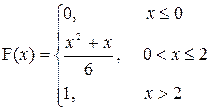
| a=1; b=5 |
23. a) При посадке на электричку пассажир проходит через турникет. Если пассажир без билета, турникет перекрывается. 8 пассажиров стоят в очереди на посадку, из них три без билета. Пусть X – число пассажиров, прошедших турникет до появления первого безбилетника. Составить закон распределения случайной величины X.
P (X≥3)
b)
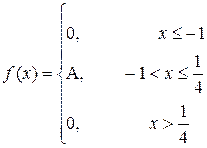
| a= –0,5; b=0,5 |
24. a) В электронной схеме, состоящей из 5 блоков, произошла неисправность в каком-то блоке. Блоки проверяют последовательно один за другим, пока не найдут неисправный блок. Пусть X – номер проверенного блока. Составить закон распределения случайной величины X.
P (1<X<3)
b)
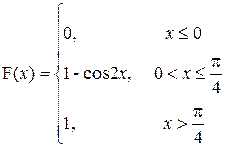
|
a=0; b= 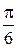
|
25. a)
| x | -3 | -1 | 0 | 1 | 2 |
| p | 0,1 | p | 0,2 | 0,2 | 0,2 |
P (–1,5<X≤1)
 b)
b)
| a=0; b=2 |
26. a)
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0,02 | p | 0,4 | 0,3 | 0,2 |
P (X>3)
b)
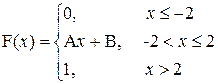
| a= –1; b=0 |
27. a) В цех по ремонту локомотивов поступило 4 партии различных приборов по 10 штук в каждой. Известно, что в каждой партии находится по 4 прибора со знаком качества. Наудачу отбираются по одному прибору из каждой партии. Найти закон распределения количества отобранных приборов со знаком качества.
P (1,5≤X<3,5)
b)
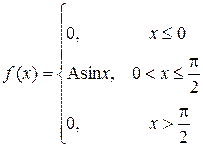
|
a= 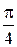 ; b= ; b= 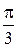
|
28. a) На городские соревнования от железнодорожной спортивной организации отбираются наугад по одному спортсмену от 3-х спортивных групп. В первой группе 10 спортсменов, из них 3 мастера спорта; во второй – 12 спортсменов, из них 4 мастера спорта; в третьей – 20 спортсменов, среди которых 5 мастеров спорта. Пусть X – число отобранных мастеров спорта. Написать закон распределения случайной величины X.
P (X≥1)
b)
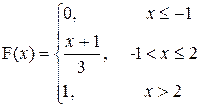
| a= –1; b=0 |
a)
| x | 1 | 2 | 3 | 5 | 7 |
| p | 0,1 | p | 0,3 | 0,35 | 0,15 |
P (2,5≤X<5)
b)
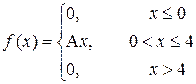
| a=3; b=¥ |
30. a) При подтверждении квалификации машиниста претендент проходит тестирование. Экзаменатор задает 4 вопроса и прекращает тестирование, если претендент не отвечает хотя бы на один вопрос. Пусть X – количество удовлетворительных ответов. Найти закон распределения случайной величины X, если вероятность ответить машинисту на один вопрос равна 0,8.
P (0≤X<2)
b)
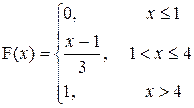
| a=0; b=2 |
Понятие вероятности. Комбинаторика
В естествознании, наряду с детерминированными процессами и явлениями, существуют такие, которые не имеют четкой причинно-следственной связи. Такие закономерности характеризуются той или иной степенью возможности (вероятности). Это связано с тем, что они описывают поведение случайных событий. Их изучением и занимается теория вероятностей.
Событие — это первичное понятие, к которому сводятся все остальные. Его можно представить как исход опыта или действия. Например, попадание стрелком в цель, выпадение цифры при бросании монеты, наступление рассвета и т.д.
Событие называется случайным, если в результате опыта (совокупности условий) оно может произойти или нет. Например, подбрасывается монета. Выпадение герба или цифры – случайное событие. Их обозначают А, В, С,… . Каждый опыт из серии опытов, повторяющихся в одних и тех же условиях, называется испытанием.
Отношение числа случаев (m), благоприятствующих наступлению события А к общему числу проведенных испытаний (n) называют относительной частотой появления события А. Обозначают W ( A ). Записывают по форме W ( A )= 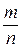 — статистическое определение вероятности. Всегда 0 ≤ W(A) ≤ 1, n — конечно.
— статистическое определение вероятности. Всегда 0 ≤ W(A) ≤ 1, n — конечно.
Когда проводится большое число испытаний, наблюдается свойство устойчивости частоты. Оно состоит в том, что частота появления события А незначительно колеблется в различных однородных сериях испытаний. Это очень важное свойство. Оно и позволяет ввести вероятность, т.е. число, около которого колеблется частота появления события А. Но часто требуется знать вероятность появления какого-либо события до проведения испытаний. Это особенно важно тогда, когда испытания трудоемки или невозможны. В таких случаях для нахождения вероятности события А пользуются классическим определением, по которому вероятность наступления события P ( A ) находится по той же формуле, что и относительная частота.
Р( A ) = 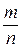 ,
,
где m — число исходов, благоприятствующих появлению события А, а n — число всех возможных исходов (событий).
Замечание: каждый из возможных исходов испытания (подбрасывание монеты, вынимание шара из урны и т.п.) называют элементарным исходом.
Формула Р(A)= 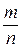 справедлива, когда исходы (события) равновозможны, несовместны и образуют полную группу.
справедлива, когда исходы (события) равновозможны, несовместны и образуют полную группу.
Под равновозможными понимают такие события, когда одно из них не более возможно, чем другое. Выпадение «6» и «3» при бросании игрального кубика — равновозможные события.
События несовместны, если в одном испытании (опыте) появление одного исключает появление других. Появление герба несовместно с появлением цифры при одном бросании монеты.
Несколько событий образуют полную группу, если в результате испытаний появится хотя бы одно из них.
Если события, образующие полную группу, попарно–несовместны, то в результате опыта появится только одно из них. Выпадение «герба» или «цифры» при бросании монеты образуют полную группу. 0 ≤ Р( A ) ≤ 1. Для достоверного события, которое в данном испытании обязательно произойдет, Р(А)=1, для невозможного Р(А)=0. Например, при бросании игральной кости выпадение числа очков меньше или равное «6» —достоверное событие, а больше «6» — невозможное.
Пример1. В урне 6 белых и 7 черных шаров. Вынимается наудачу один шар. Найти вероятность того, что он белый.
Решение. Число всех случаев вынуть один шар равно сумме шаров в урне 6+7=13, причем исходы равновозможны, несовместны и образуют полную группу. Пусть событие А — вынут белый шар. Число случаев, благоприятствующих этому событию m=6, т.к. белый шар можно вынуть только из белых шаров. Поэтому Р(А)= 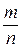 =
= 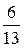 .
.
Но формулы W(A) и P(A), справедливы только при конечном числе испытаний (исходов) (n). Чтобы восполнить этот недостаток вводят понятие геометрической вероятности, т.е. вероятности попадания точки в область (отрезок, площадь, …)
Р(А)= 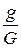 , где g принадлежит G и g — мера геометрического образа (длины, площади, …), благоприятствующего попаданию точки; G — мера всей рассматриваемой области.
, где g принадлежит G и g — мера геометрического образа (длины, площади, …), благоприятствующего попаданию точки; G — мера всей рассматриваемой области.
Часто подсчитать число всех исходов или число благоприятствующих случаев бывает не так просто или трудоемко. Здесь на помощь приходит комбинаторика — раздел математики. Она изучает различные способы соединения элементов в группы: перестановки, размещения, сочетания.
Перестановками (P n ( n ) ;Р n) из n элементов называют их соединения, которые различаются друг от друга только порядком входящих в них элементов.
Размещениями (A 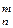 ) из n элементов по m называют такие их соединения, которые различаются друг от друга самими элементами или их порядком.
) из n элементов по m называют такие их соединения, которые различаются друг от друга самими элементами или их порядком.
Сочетаниями (C 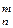 ) из n элементов по m называют соединения элементов, которые отличаются друг от друга только самими элементами.
) из n элементов по m называют соединения элементов, которые отличаются друг от друга только самими элементами.
Дата: 2019-12-09, просмотров: 1346.