Формула Бернулли
Пусть проводится n независимых испытаний. В каждом из них вероятность появления события А равна р. Найти вероятность того, что среди n независимых испытаний событие А появится ровно k раз (Рn (k)).
Вероятность одноразовому событию А произойти k раз и не произойти (n – k) раз равна pk ×qn-k , где q=1–p
Число таких событий задается числом способов наступления события А, то есть равно числу сочетаний из n испытаний по k ( 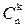 ).
).
Тогда, искомая вероятность равна
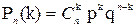
Это и есть формула Бернулли.
Пример 19. Найти вероятность того, что в 6 независимых испытаниях событие А появится 2 раза, если в каждом испытании вероятность его появления равна р=0,3.
Решение. n = 6; k=2; р=0,3; q=1–р=0,7.
Одно сложное событие состоит в том, что событие А наступит 2 раза и не наступит 4 раза. Его вероятность равна
0,32×(1–0,3)4=0,32×0,74
Число таких случаев 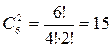
Тогда, вероятность того, что событие А наступит 2 раза в 6 испытаниях равна
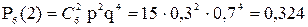
Пример 20. Стрелок стреляет по мишени 8 раз. Вероятность попадания при каждом выстреле 3/4. Найти вероятность того, что он попадет в мишень не менее 2х раз.
Решение. n = 8; k³2; р= 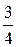 ; q=1–р=
; q=1–р= 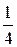 .
.
Событие А – стрелок попал в мишень не менее 2-х раз. Значит он попал в мишень или 2, или 3, … или 8 раз. Тогда, по теореме сложения вероятностей несовместных событий
Р8(k³2)= Р8(2)+ Р8(3)+ Р8(4)+…+ Р8(8)
Но подсчитывать все вероятности – процесс трудоемкий. Проще подсчитать вероятность противоположного события
Р8(k<2)= Р8(k=0)+ Р8(k=1)
Тогда Р8(k³2)= 1– Р8(k<2)
т.е.
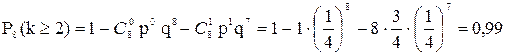
Если число испытаний, (n) велико, то вычисления по формуле Бернулли громоздки. В этом случае применяют приближенные формулы Муавра-Лапласа или Пуассона.

Пример 21. Найти вероятность того, что при 40 выстрелах стрелок поразит мишень 30 раз. Вероятность поражения стрелком мишени при одном выстреле р=0,8.
Решение. n = 40; k=30; р=0,8; q=1–р=0,2
Так как вычисления по формуле Бернулли громоздки, воспользуемся формулой Муавра-Лапласа.
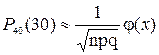
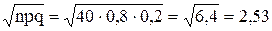
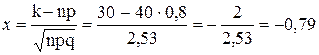
В таблице значений четной функции 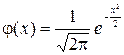 находим j(–0,79)= j(0,79)=0,2920
находим j(–0,79)= j(0,79)=0,2920
Тогда 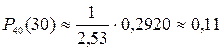
Пример 22. На железнодорожном вокзале кассир обслуживает в течение недели 600 пассажиров. Вероятность ошибки в оформлении билета равна 0,003. Какова вероятность того, что будет оформлено неверно а) 2 билета? б) не больше 2-х билетов.
Решение . n = 600; р=0,003; k1=2; k2£2;
Т.к. np=l=1,8<10, воспользуемся формулой Пуассона для вычисления вероятности
а) 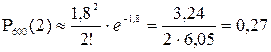
б) 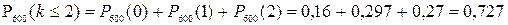
Когда требуется вычислить вероятность наступления события А не менее k1 раз и не более k2 раз можно воспользоваться точной формулой
P(k1 £ n £ k2)=Pn(k1)+Pn(k1+1)+…+Pn(k2)
или, во избежание громоздких вычислений (при k1>10), приближенной формулой Лапласа (интегральной теоремой Лапласа)
P(k1 £ n £ k2)=Ф(x//)–Ф(x/), где
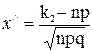 ;
; 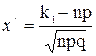
где 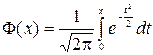 – нечетная ( табулированная)
– нечетная ( табулированная)
Пример 23. Вероятность поражения мишени стрелком при одном выстреле 0,6. Найти вероятность того, что из 50 выстрелов мишень будет поражена не менее 30 и не более 40 раз.
Решение . n=50; k1=30; k2= 40; p=0,6; q=1–0,6=0,4
Дата: 2019-12-09, просмотров: 387.