| Без повторения элементов | С повторениями (возвращениями) элементов |
| Перестановки | |
| P(n) = n! |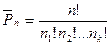 
n 1 , n 2 , … nk — число повторений соответствующих элементов
|
Размещения
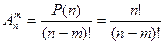
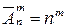
Сочетания
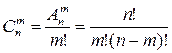
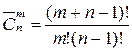
Пример 2. Найти число перестановок из трех цифр 1, 2, 3.
Решение. 123, 132, 231,213, 321, 312 или P3 = 3! = 1· 2· 3=6.
Пример 3. Найти число перестановок из букв слова «потоп».
Решение. P5 =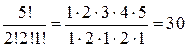 
, так как в слове «потоп» 2 буквы «п», 2 буквы «о» и одна буква «т».
Пример4. Найти число размещений из четырех цифр 1, 2, 3, 4 по две.
а) без повторения цифр;
б) с повторениями их.
Решение. а) 12 13 14 21 23 24
31 32 34 41 42 43
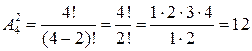
б)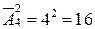 
Пример 5. Найти число сочетаний из четырех элементов a , b , c , d по два
а) без повторения элементов;
б) с повторениями.
Решение. а)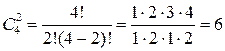 
б)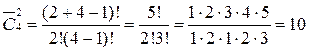 
Здесь ab и ba неразличимы.
Замечание: В каждой конкретной задаче выбор формулы для подсчета m и n определяется ее содержанием.
Пример 6. На автодороге Красноярск–Дивногорск за время t зарегистрирован проезд 1000 автомобилей. Из них 6 инициировали дорожно-транспортные происшествия. Найти относительную частоту аварий автомобильного транспорта на этом участке.
Решение. Событие А—«произошло дорожно-транспортное происшествие». Тогда частота появления события А
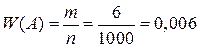
Пример 7. В урне a белых и b черных шаров. Наудачу выбирают три шара. Найти вероятность того, что они все черные.
Решение. Событие А—«вынуты 3 черных шара». Общее число равновозможных исходов испытания равно числу способов, которыми можно извлечь три шара из общего числа (a + b) шаров, т.е. числу сочетаний из (a + b) по 3: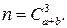 
Найдем число исходов, благоприятствующих событию А: вынуть три черных шара. Так как черные шары можно взять только из черных, то число способов вынуть три черных шара равно числу сочетаний из b черных шаров по 3: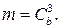 
Тогда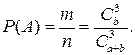 
Здесь для подсчета m и n применили формулы сочетаний, так как порядок взятых трех шаров нас не интересует.
Пример 8. На отрезке [0,3] оси Ox называется произвольное число. Найти вероятность того, что оно будет принадлежать части этого отрезка [1,3].
Решение. Пусть событие А – «число принадлежит отрезку [1,3]». В задаче пространство всех равновозможных элементарных событий (G) имеет размер длины отрезка и равно 3, а пространство элементарных событий, благоприятствующих наступлению события А (g), равно 2 — длине отрезка[1,3].
Тогда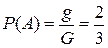 
Задания
a) Человек решил поехать на день рождения к своему другу. Но к нему можно добраться только с пересадкой в городе А. Сначала у него есть три варианта поездки: поездом, автобусом пароходом, а дальше до места назначения только вертолетом или на моторной лодке. Сколькими способами человек может добраться к своему другу?
b) Сколько различных перестановок можно составить из букв слова «демократия», «крокодил»?
c) Сколькими способами можно разместить 8 человек в двух купе, если Нина и Оля должны быть в одном купе?
d) Проводник разносит пассажирам чай. В его распоряжении 9 купе по 4 человека в каждом. Сколькими способами он может обслужить их?
e) Серебренная, золотая и бронзовая медали разыгрываются между десятью штангистами. Сколькими способами медали могут быть распределены?
f) Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, если цифры
g) не повторяются
h) повторяются?
i) Сколькими способами можно распределить на пароходе среди шести человек
j) 3 одноместные каюты I класса?
k) Одну каюту «люкс», одну одноместную I класса и одну одноместную II класса?
l) Сколькими способами можно разместить на стоянке автомобилей на лучшее место сначала 2 «Нивы» из 5, потом 3 «Мерседеса» из 5, а затем остальные машины? Всего в очереди на размещение 16 машин.
m) В урне 5 белых и 4 красных шара. Сколькими способами можно достать 3 белых шара? Сколькими способами можно достать любые 3 шара?
n) На верхней полке в купе можно разместить 4 багажных предмета. Сколькими способами это можно сделать? Сколькими способами их можно расставить на двух верхних полках?
o) В магазине покупатель может приобрести для себя 10 различных предметов одежды. Сколькими способами он может купить 2 разные по составу комплекта одежды из 8 предметов?
p) Из 100 подбрасываний монеты «герб» выпал 48 раз. Какова относительная частота появления «герба»?
q) На испытательном стенде проходят проверку на виброустойчивость 100 приборов. Относительная частота годных приборов оказалась равной 0,93. Найти число бракованных приборов.
r) На работу проводником требуются пять человек. Подали заявление 8 человек, из них 5 женщин. Найти вероятность того, что будут отобраны двое мужчин и три женщины.
s) В соревнованиях по парному фигурному катанию на зимних олимпийских играх разыгрываются медали золотая, серебряная и бронзовая. В розыгрыше участвуют спортсмены из Англии, Финляндии, Германии, США, Белоруссии и России. Каждая страна представляет по 2 пары участников. Какова вероятность того, что золотая медаль достанется России, серебряная – Белоруссии и бронзовая – Финляндии.
t) На 6 карточках написаны цифры 1, 3, 4, 6, 7, 9. Наугад берутся 2 карточки и составляется дробь. Какова вероятность того, что ее можно сократить на три?
u) В редакции газеты работают 7 корреспондентов. Редактор для беседы приглашает троих из них. Найти вероятность того, что корреспонденты будут вызваны в определенном порядке?
v) На прилавке магазина 60 одинаковых тетрадей в клетку. Из них 20 сделаны из бумаги второго сорта. Покупатель приобрел 15 тетрадей, из них 6 оказались второго сорта. Он решил купить ещё одну. Какова вероятность того, что эта тетрадь будет второго сорта?
w) В библиотеку института поступили 20 учебников по английскому языку. Из них три оказалось с браком. Для занятий в группе берут 7 учебников. Какова вероятность того, что среди них окажется один бракованный?
x) Секретный замок сейфа содержит шифр из пяти разных цифр. Оператор забыл первую цифру и набрал её наудачу. Какова вероятность того, что будет набрана верная цифра? Какова вероятность открыть сейф, если он забыл 3 первые цифры и набирает их наудачу?
y) В ремонтный цех поступило 12 осей для колесных пар. Из них три дефектные. Рабочий берет наудачу 2 оси. Найти вероятность того, что взята одна стандартная и одна дефектная ось.
z) Из букв слова «коммутатор», нанесенных на карточки, последовательно берется 5 букв и складываются в ряд. Какова вероятность того, что получится слово «мотор».
aa) У ребенка есть буквы нарезной азбуки и, о, у, з, н, к, м, м, м. Какова вероятность того, что раскладывая их подряд, он получит слово «коммунизм»?
bb) Из 50 взятых наудачу подшипников, оказались бракованными несколько штук. Частота появления брака 0,1. Сколько было бракованных подшипников?
cc) Квадрат с вершиной в начале координат и стороной 3 см пересекается с параболой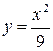 
. Какова вероятность того, что наудачу брошенная точка попадет на участок квадрата, лежащий вне площади, ограниченной параболой?
dd) Пять человек разного роста выстраиваются в одну линию. Найти вероятность того, что они выстроятся строго в убывающем порядке.
ee) В квадрат со стороной 3 см вписан круг радиуса 1 см, произвольно. Найти вероятность того, что точка брошенная в квадрат, окажется в круге.
ff) В окружность радиуса 5 см вписан квадрат. Наудачу брошена в круг точка, которая попадает в квадрат, вписанный в круг, с вероятностью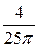 
. Найти сторону квадрата.
gg) Две параболы y = x2 и x = y2 пересекаются в точках (0,0) и (1,1) квадрата со стороной в 1 см, две стороны которого лежат на осях координат. Какова вероятность брошенной наудачу точке попасть на участок, ограниченной параболами?
hh) Подбрасываются две игральные кости белая и черная. Найти вероятность того, что на белой кости выпало не меньше 3 очков, а на черной – кратное трем.
ii) Два встречных поезда приходят в Красноярск с 10 до 11 часов. Стоянка каждого 15 минут. Каждый может прибыть с опозданием. Какова вероятность встречи поездов?
jj) Какова вероятность получить из слова «комбинация» слово, состоящее из двух гласных и трех согласных?
kk) Из пяти пронумерованных кубиков наудачу извлекают по одному три кубика. Найти вероятность того, что номера кубиков расположены в возрастающем порядке.
ll) На карточках написаны буквы э, л, е, р, т, о, з, в, о, к. Ребенок берет по одной и раскладывает их в ряд. Какова вероятность того, что получится слово «электровоз»?, слово «лектор»?
mm) Набирая номер телефона, абонент забыл две последние цифры, но помнит, что они разные. Абонент стал набирать их наудачу. Какова вероятность того, что абонент наберет нужный номер со второго захода?
nn) В ящике лежат 12 одинаковых тетрадей. Из них пять в линейку, остальные – в клетку. Взяты наудачу 3 тетради. Найти вероятность того, что из них хотя бы одна окажется в клетку.
oo) В коробке лежало несколько лампочек, причем две из них на 127 в, а остальные на 220в. Вероятность взять три лампы, из которых одна на 127 в, а две другие на 220в равна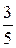 
. Найти число лампочек в коробке.
pp) Рыбак поймал 8 омулей и хариусов, примерно одинаковых по весу. Покупатель с вероятностью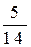 
покупает у него 2 омуля. Сколько омулей и хариусов поймал рыбак?
Дата: 2019-12-09, просмотров: 563.
