Обработки результатов социологических
И маркетинговых исследований
В результате проведённых социологических исследований накопляется достаточно большой объём информации (данных), который требует обработки. Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Процедуры здесь сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения (например, средней арифметической) и, наконец, к оценке разброса данных по отношению к найденной центральной тенденции. Корректность в применении этих методик обеспечивается не только содержательными представлениями, но и выполнением особых требований – требований валидности, надёжности, репрезентативности тестовых норм.
Что касается количественных данных, то они всегда располагаются на непрерывной шкале и, как правило, весьма многочисленны. Поэтому такие данные предпочитают группировать по классам, чтобы яснее видна была основная тенденция распределения.
По проведённым опросам-тестам проводится группировка, состоящая в основном в том, что объединяются данные вопросов с одинаковыми или близкими значениями в классы и определяются частоты для каждого класса. Способ разбиения на классы зависит от того, что именно необходимо выявить при разделении измерительной шкалы на равные интервалы (рис. 22).
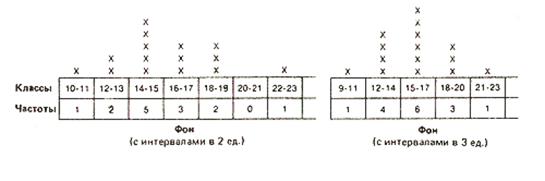
Рис. 22. Графическое распределение частот по классам
(источник: по материалам [36])
Выбор того или иного типа группировки зависит от различных соображений. Например, группировка с интервалами между классами в две единицы хорошо выявляет распределение результатов вокруг центрального «пика». В то же время группировка с интервалами в три единицы обладает тем преимуществом, что даёт более обобщённую и упрощённую картину распределения, особенно если учесть, что число элементов в каждом классе невелико. При большом количестве данных число классов по возможности должно быть где-то в пределах от 10 до 20, с интервалами до 10 и более. Данные, разбитые на классы по непрерывной шкале, нельзя представить графически так, как это сделано выше. Поэтому предпочитают использовать так называемые гистограммы – способ графического пред-ставления в виде примыкающих друг к другу прямоугольников (рис. 23).
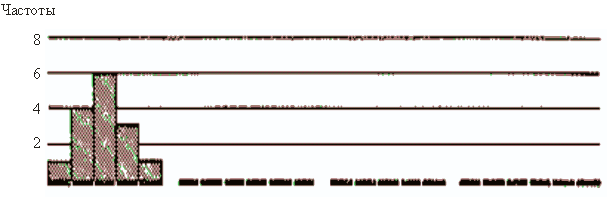
| 9–11 | 12–14 | 15–17 | 18–20 | 21–23 | 9–10 | 11–13 | 14–16 | 17–19 | 20–22 | 23–25 | 8–10 | 11–13 | 14–16 | 17–19 | 20–22 | 5–7 | 8–10 | 11–13 | 14–16 | 17–19 | 20–22 |
Рис. 23. Гистограмма разбиении на классы по непрерывной шкале
(источник: по материалам [36])
Наконец, для ещё более наглядного представления общей конфигурации распределения можно строить полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. При этом получают следующую картину (рис. 24).
| 9–11 | 12–14 | 15–17 | 18–20 | 21–23 | 5–7 | 8–10 | 11–13 | 14–16 | 17–19 | 20–22 |
Рис. 24. Полигоны распределения частот
(источник: по материалам [36])
Для того чтобы подробнее выразить тенденции распределения, количественно используются три вида показателей: средняя, мода, медиана.
1. Мода (Мо) – это самый простой из всех трёх показателей. Она соответствует либо наиболее частому значению, либо среднему значению класса с наибольшей частотой.
Мода используется редко и главным образом для того, чтобы дать общее представление о распределении. В некоторых случаях у распределения могут быть две моды; тогда говорят о бимодальном распределении (рис. 25). Такая картина указывает на то, что в данной совокупности имеются две относительно самостоятельные группы.
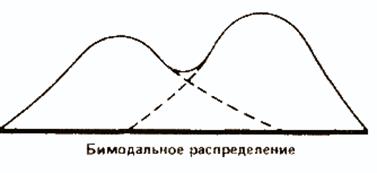
Рис. 25. Бимодальное распределение
(источник: по материалам [36])
2. Медиана (Me) соответствует центральному значению в последовательном (ранжированном) ряду всех полученных значений. В случае если число данных n, четное, медиана равна средней арифметической между значениями, находящимися в ряду на n/2-м и n/2+1-м местах.
3. Средняя арифметическая (М) (далее просто «средняя») – это наиболее часто используемый показатель центральной тенденции. Её применяют, в частности, в расчётах, необходимых для описания распределения и для его дальнейшего анализа. Её вычисляют, разделив сумму всех значений данных на число этих данных.
Ещё одним показателем, который можно использовать в описательной статистике опросов-тестов, является величина разброса. Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от средней, обозначаемое буквой d, а затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Напротив, если эта средняя невелика, то данные больше сконцентрированы относительно их среднего значения и выборка более однородна. Первый показатель, используемый для оценки разброса, – это среднее отклонение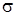 
. Его вычисляют следующим образом. Собрав все данные и расположив их в ряд, находят среднюю арифметическую для выборки. Затем вычисляют отклонения каждого значения от средней и суммируют их:
= 
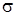. (6)
Поскольку стандартное отклонение всегда соответствует одному и тому же проценту результатов, укладывающихся в его пределах вокруг средней, можно утверждать, что при любой форме кривой нормального распределения та доля её площади, которая ограничена (с обеих сторон) стандартным отклонением, всегда одинакова и соответствует одной и той же доле всей популяции.
Описательная статистика позволяет продемонстрировать, как можно представить графически и оценить количественно степень разброса данных в том или ином распределении. Тем самым можно понять, чем различаются распределения для контрольной группы до и после воздействия. Однако можно ли о чём-то судить по этой разнице – отражает ли она действительность или же это просто артефакт, связанный со слишком малым объёмом выборки? Тот же вопрос встаёт и в отношении экспериментальной группы, подвергнутой воздействию независимой переменной. В этой группе стандартное отклонение для фона и после воздействия тоже различается примерно. Разница между средними показывает достоверность в данных, позволяет ответить на вопрос о возможности опираться на эти результаты и распространять их на всю выборку. На все эти вопросы и пытается дать ответ: индуктивная ли описательная статистика.
Массовая экспресс-диагностика. Здесь не исключены ошибки в индивидуальных случаях, диагноз и прогноз даются лишь с вероятностной точностью [36].
Эти приёмы позволяют проверить, «работает» ли тест в целом и, если он плохо дифференцирует испытуемых, в каких своих частях (заданиях, вопросах) тест «не срабатывает». Применение этих приёмов полезно и необходимо не только при разработке новых тестов, но и при всяком изменении диагностической ситуации в применении старого теста, при переносе теста с одной популяции (на которой установлены тестовые нормы) на другую. Это, прежде всего, относится к техникам самоотчёта и, в частности, к тест-опросникам, полностью зависящим от того, как конкретный испытуемый интерпретирует семантику вопросов и связывает её с субъективной гипотезой о цели обследования.
В социальном маркетинге широко применяются разного рода опросы и тесты. Тест-опросник состоит, как правило, из так называемых ли-вопросов, или «да-нет»-вопросов: каждый вопрос содержит утверждение, с которым испытуемому предлагается соглашаться или не соглашаться. В результате ответ испытуемого кодируется как дихотомическая переменная со значениями «+1» («верно») и «-1» («неверно»). Балл теста подсчитывается суммированием ответов «верно» на «прямые» пункты теста (это вопросы, позитивно связанные с измеряемой чертой) и ответов «неверно» на «обратные» пункты (вопросы, негативно связанные с измеряемой чертой).
Алгебраически такой простейший способ подсчёта тестового балла может быть описан формулой:
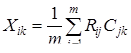, (7)
где Хik – балл i-го испытуемого по k-й шкале (черте); Rij – ответ i-го испытуемого на j-й пункт тест-опросника; Cjk – ключ (шкальное значение) j-го пункта по k-й шкале; m – количество пунктов в k-й шкале (для которых Сjk = 0).
Обычно Rij = {-1,+1} и Cjk={-1, 0, +1}.
Чтобы как-то минимизировать и без того большие погрешности тест-опросника, необходимо понимать психологический смысл этой процедуры. Пункт тест-опросника должен являться эмпирическим индикатором диагностического концепта – личностной черты. Некорректные вопросы следует исключать из перечня.
Прежде чем применить какой-то тест-опросник на особом контингенте лиц, необходимо постараться взглянуть на каждый вопрос глазами испытуемого. Это требует немалой профессиональной интуиции. При наличии большинства вопросов добиться полной имитации ответов испытуемых не удаётся. В данных случаях применяют эмпирико-статистиче-ский анализ пунктов (в зарубежной тестологии утвердился особый термин – «item analysis»).
В настоящее время без применения этого аппарата не обходится ни одна серьёзная попытка конструирования или адаптации тестов и опросов.
Аппарат эмпирико-статистического анализа пунктов открывает возможность для приспосабливания методики к конкретным условиям её применения. Эта возможность состоит в модификации шкальных ключей для отдельных пунктов (значений Сjk). Обычная архаическая доизмерительная стратегия такого приспособления состоит в том, что опросчик переформулирует сам вопрос в случае его некорректности в рассматриваемой ситуации. Таким образом, перечень вопросов изменяется. Результаты, полученные от респондентов из крупных и небольших городов, оказываются несопоставимыми [36].
Противоположная тактика состоит в том, чтобы перечень вопросов оставлять неизменным, но в разных случаях пользоваться разными векторами шкальных ключей <С>. (Во всех случаях задаются оба вопроса. Этот подход позволяет соединить две задачи конструирования теста: отбор информативных признаков и построение шкалы (уточнение градуального Cjk). При этом неккоректный вопрос будет иметь Сjk = 0.0 в маленьком городе (где k – шкала «тревожности») и, наоборот, Сjk = +1.0 в большом.
Эмпирически устанавливать значения Сjk в отсутствии компьютера, помогает простейший метод.
Алгоритм четырехклеточной корреляции [2].
Идеи этого алгоритма в разнообразных модификациях использовались во множестве работ зарубежных и отечественных авторов. В ситуации, возникающей в отсутствие внешнего критерия валидности, имеется тест-опросник, ориентированный на измерение какой-то одной личностной черты (одномерный опросник) и содержащий М вопросов. Об опрашиваемом контингенте не имеется никакой априорной эмпирической информации, предполагается, что индивиды в этой выборке значимо отличаются между собой по степени выраженности рассматриваемой черты k. Опросчик хочет приспособить тест-опросник к измерению черты k на данном контингенте с помощью уточнения шкальных ключей Cjk. Для этого ему целесообразно взять для предварительного исследования случайную выборку из N индивидов.
На сформированной выборке экспериментатор проводит обследование и получает массив результатов в виде прямоугольной матрицы размерностью N×М, где по строкам испытуемые, по столбцам – пункты, на пересечении – значения Rij ответов i-го испытуемого на j-й вопрос тест-опросника.
Для каждого столбца (для каждого пункта) экспериментатор на основании исходных предположений назначает С0jk – исходные шкальные ключи. Затем для каждой строки (каждого испытуемого) матрицы |R| по формуле (8) подсчитывается суммарный тестовый балл Хik. Среди всех {X} отыскивают 30 % испытуемых с наибольшими значениями тестового балла и 30 % – с наименьшими. Они включаются соответственно в «высокую» и «низкую» экстремальную группы. В дальнейшем по каждому пункту учитываются только ответы испытуемых из экстремальных групп. Шкальные ключи Сjk уточняются с помощью расчёта четырехклеточной корреляции между ответами на пункт и попаданием в экстремальную группу. Для каждого пункта строится матрица сопряжённости 2×2 (рис. 26):
| Экстремальная группа | ||
| Ответ | Высокая | Низкая |
| «Верно» | a | b |
| «Неверно» | c | d |
Рис. 26. Матрица сопряжённости
(источник: составлено автором)
В клеточках таблички 2×2 указываются частоты. Например, в клеточке а суммируется частота встречаемости тех испытуемых, которые попали в «высокую» группу и ответили «верно» на данный j-й пункт опросника, в клеточке b – число испытуемых из «низкой» группы, ответивших «верно», и т.п. Очевидно, что «хороший» пункт, обладающий высокой дискриминативностью относительно экстремальных групп, должен обладать высоким контрастом значений a и b, с одной стороны, и одновременно высоким контрастом с и d – с другой. При этом контрасты должны иметь противоположный знак: если а больше b («верно» чаще отвечает «высокая» группа), то с должно быть меньше а («неверно» чаще отвечает «низкая» группа); наоборот, в случае «обратных» пунктов, когда разность а -b отрицательна, то разность с -d должна быть положительна.
Существуют различные коэффициенты, которые учитывают эти требования:
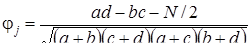, (8)
где N – сумма всех элементов таблички: N = a+b+c+d.
Так как при использовании равных и известных по объёму экстремальных групп а+с = b+d = S, формула (9) несколько упрощается:
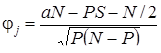, (9)
где Р – сумма ответов «верно» на данный пункт: Р=а+b.
Значимость фи-коэффициента устанавливается из следующего приближённого соотношения:
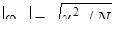(10)
где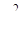 
– стандартный квантиль распределения икс-квадрат с одной степенью свободы.
Таким образом, если при выборке N=100 вычисленное значение фи-коэффициента превышает по модулю 0,26, то это означает, что с пренебрежимой вероятностью ошибки в 1 % можно делать вывод о том, что данный пункт вносит значимый вклад в суммарный балл.
В отсутствие полного совпадения требуется выполнить новый цикл вычислительной обработки. По уточнённому вектору – ключу <С1> по формуле (1) вновь подсчитываются суммарные баллы для всех испытуемых. Затем опять определяются экстремальные группы, вновь подсчитываются фи-корреляции для всех М пунктов опросника. (Если сразу несколько испытуемых на границе между экстремальной и нейтральной группой набрали одинаковый балл, то следует всех испытуемых с одинаковым баллом включить в одну группу, добиваясь, чтобы экстремальная была ближе к 30 %, тогда численности экстремальных групп могут быть неодинаковы.) Очевидно, что процедура достигает результативной остановки, если <Ct> = <Ct+1>, т.е. когда ключ, полученный на очередном шаге обработки, совпадает полностью (по всем j) с ключом, полученным на предыдущем шаге.
В данном случае этот момент можно определить заранее: искомое условие достигается уже тогда, когда стабилизируются составы «высокой» и «низкой» групп (а именно составы экстремальных групп определяют значения фи-корреляции). Для оценки качества пунктов часто применяют более трудоёмкую в вычислительном отношении точечно-бисериальную корреляцию. В этом случае остановиться можно при равенстве ct+1ik = ctik. Сравнение результатов этого алгоритма с более точными компьютерными алгоритмами (например, факторный анализ по методу главных компонент) показывает, что достигается удовлетворительное соответствие «ручных» и «компьютерных» ключей в среднем уже на пятом-шестом шаге приближения.
Сходимость (скорость стабилизации вектора <Сtjk>) данного алгоритма зависит от степени разработанности самого опросника. Этот алгоритм быстро приводит к выделению устойчиво полезных пунктов, если большинство пунктов опросника хороши. Наоборот, если таких пунктов меньше половины, то процедура затягивается. В этом случае лучше остановить процесс обсчёта уже после первого приближения <С'> и, если найдено слишком мало значимых jj, заняться переформулированием старых или добавлением новых вопросов (после чего проводить новое обследование).
При отборе пунктов по внешнему критерию (при построении теста по критерию или адаптации вопросника к другой проблеме) описанные простые вычислительные приёмы также могут быть применены.
К сожалению, при отборе пунктов по критерию редко выполняется обязательное правило «перекрёстной валидизации»: полученные значения jj должны быть проверены на независимой выборке (или на половине целой выборки). Также редко учитывается, к сожалению, что построение теста по критерию – это прагматическая стратегия, которая не обеспечивает психологической однородности измеряемого конструкта: в ключ <С> могут быть включены психологически различные факторы. Тест-опрос-ники, построенные по внешнему критерию, при последующей факторизации, как правило, «распадаются» на ряд независимых факторов. С этой точки зрения, оптимальную тестовую батарею (набор пунктов) по критерию можно получить, применяя анализ множественных корреляций: весовые коэффициенты bj для каждого пункта в уравнении множественной регрессии «очищены» от неоправданного (с точки зрения экономичности) дублирования пунктов, слишком тесно коррелированных друг с другом. Но вычислительная трудоёмкость этого метода требует обязательного использования компьютера, уже когда М > 5.
Алгоритм раздельного коррелирования ответов.
Преимущества – в ещё большей простоте вычислений, более быстрой и более высокой дифференцирующей силе построенной шкалы.
При том же уровне структурированности массива |R| сходимость ключей достигается за счет 3-4 итераций. Выделенный вектор опять же высоко конгруэнтен (совпадает) с первой или второй главной компонентой одномерного опросника. При факторизации одномерного опросника практически всегда выделяются два фактора: один соответствует измеряемому свойству, другой – социальной желательности ответа; сила второго фактора зависит от диагностической ситуации и уровня подозрительности контингента испытуемых.
Алгоритм раздельного коррелирования ответов, подобно очень сложным алгоритмам латентно-структурного анализа, позволяет учитывать при подсчёте суммарного балла с разным весом ответы «верно» и «неверно»:
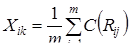, (11)
где C(Rij) – ключ, заданный как вторичная переменная, принимающая различные значения в зависимости от того, какое из заранее предусмотренных значений Rij реализовано. Такая модификация позволяет учесть разную силу ответов «верно» и «неверно», их разное диагностическое значение.
На каждом очередном t-м шаге вычислений по ключу <Ct-1ik> и по матрице |R| с помощью формулы (12) подсчитываются суммарные баллы xik. Как и в первом алгоритме, выделяются «высокая» и «низкая» группы, и для каждого j-го пункта строится четырёхклеточная табличка сопряжённости. Ключ для ответа «верно» определяется по формуле:
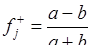, (12)
где f+j достигает +1, если «верно» отвечают только представители «высокой» группы, и -1, если «верно» отвечают только испытуемые из «низкой» группы. Значимость f+j можно оценить с помощью следующего приближенного соотношения:
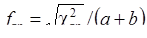. (13)
Ключ для ответа «неверно» определяется по формуле:
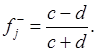(14)
Проверка значимости f-j аналогична с учётом подстановки c+d=a+b.
В компьютерном варианте легко использовать ключи, принимающие всевозможные значения на отрезке [-1, +1], т.е. приравнивать C(Rjk) = fjk. При ручных вычислениях лучше применить целочисленную семибалльную шкалу [-3, +3] с формулой перехода Cjk = 3 fjk и округлением до ближайшего целого. Конечно, присваивать пунктам Cjk, отличные от нуля, нужно только в том случае, если fj значимо превышает fгр по модулю.
Практическое испытание данного алгоритма показало, что более высокими fj, как правило, обладают менее социально одобряемые ответы.
Достоинство второго алгоритма в том, что он позволяет отыскать значимые связи там, где первый алгоритм фиксирует только незначимую корреляцию.
3 Комплекс маркетинга – как совокупность направлений реализации
маркетинговой деятельности в учреждениях пенитенциарной системы
3.1 Обоснование необходимости использования маркетингового подхода к управлению экономической деятельностью данных учреждений
Маркетинг включает в себя множество самых разнообразных видов деятельности, в том числе маркетинговые исследования, разработку товара, организацию его распространения, установление цен, рекламу и личную продажу. Маркетинг – это процесс, в ходе которого разрабатываются и предоставляются в распоряжение людей товары и услуги, обеспечивающие определённый уровень жизни. Маркетинг сочетает в себе несколько видов деятельности, направленных на выявление, обслуживание, удовлетворение потребительских нужд для решения целей, стоящих перед организацией. Маркетинг начинается задолго до и продолжается ещё долго после акта купли-продажи.
Практическая ипостась маркетинга состоит в выработке конкретных рекомендаций по различным аспектам производственно-коммерческой деятельности фирм и нацелена на решение таких задач, как анализ и изучение рынков, позиционирование продуктов, ценообразование, товарно-распределительная политика, реклама и управление сбытом. Маркетинг применим не только к классическим «рыночным предприятиям», но даже и к таким специфическим промышленным объектам, как уголовно-испра-вительные колонии.
Но пенитенциарная система не всегда была связана с маркетингом. История применения маркетингового подхода к развитию производственного сектора пенитенциарной системы начинается в 1990 г. В то же время правительство России стало приводить экономику станы к рыночным отношениям. Исходя из этого можно представить историю развития производственного сектора пенитенциарной системы в форме поэтапного преобразования маркетинговой деятельности производственного комплекса пенитенциарной системы (рис. 27).
Каждое предприятие в колонии – самостоятельное юридическое лицо, имеющее право работать на рынке. Наиболее распространённая форма сотрудничества колоний с коммерсантами – лизинг. Компания приобретает оборудование, устанавливает его на зоне и обучает заключённых работать. А затем зона расплачивается за него продукцией, которая на нем производится.
Рис. 27. Этапы развития маркетинговой деятельности
производственного комплекса пенитенциарной системы
(источник: составлено автором)
Чтобы разместить заказ на изготовление товаров в «тюремной корпорации», нужно связаться с отделом маркетинга и материально-техни-ческого снабжения производства УФСИН России в конкретной области. Работники отдела обещают посоветовать те учреждения, которые выпускают нужный продукт. Если же учреждение заранее известно, обращаться можно непосредственно в отдел маркетинга конкретной зоны.
Отделы маркетинга некоторых колоний заявили, что их предприятия готовы взаимодействовать с бизнесом по нескольким направлениям: заказы на изготовление различных видов продукции, создание контрагентских участков и совместных производств на базе предприятий пенитенциарной системы, а также разработка и внедрение совместных инвестиционных проектов. И все предприятия исправительных учреждений готовы рассмотреть возможность освоения на имеющейся производственной базе новых видов изделий и новых производств.
Главное преимущество колониальных производств – в многопро-фильности их сотрудничества с клиентами. Такое производство может быстро и гибко реагировать на изменения рынка: перестаёт продаваться один товар, в колонии налаживается производство других товаров. Рентабельность некоторых колоний может достигать 15 %. Но существуют и естественные ограничения в номенклатуре выпускаемых в колониях товаров.
В связи с тем, что предприятия пенитенциарной системы – это режимные объекты, предприниматели при размещении заказов могут столкнуться с некоторыми неудобствами в работе. Прежде всего, налагаются ограничения на номенклатуру выпускаемых изделий: исключено производство спиртосодержащих жидкостей, наркотических веществ, оружия и т.п. Кроме того, пропускной режим учреждений предусматривает досмотр транспорта и людей на наличие запрещённых веществ и предметов, в том числе сотовых телефонов и фотоаппаратов.
В поисках клиентов сотрудники отделов маркетинга колоний посещают промышленные выставки и ярмарки, рассказывая всем интересующимся о товарах, производимых заключёнными. Специально предприниматели не ищут свободные производственные площади в колониях. Арендных площадей достаточно на «воле». Заинтересованность в привлечении труда заключённых бизнесмены проявляют только тогда, когда могут изучить цены на товары и услуги, поставляемые колониями. Законы рынка одинаковы для всех субъектов, действующих на нём. Поэтому для тюремного бизнеса реклама так же важна, как и для любого другого предприятия.
В колониях множество свободных производственных площадей с работающими инженерными коммуникациями, энерго-, водо- и теплоснабжением. Сырье и товары находятся под особым режимом охраны. Хищения продукции собственными работниками исключено. Заключённые являются уникальной рабочей силой, которая постоянно находится на производстве и не требует затрат на социальное обеспечение – «социальным пакетом» заключённых распоряжается государство. В остальном, колониальные производства являются обычными предприятиями. Ещё одно преимущество основано на «эффекте экономии от масштаба» выпускаемой продукции – колонии могут обеспечить большие объёмы по сравнительно низким ценам.
В связи с проводимыми в колониях преобразованиями, исправительной системе требуется дополнительное финансирование. Так как бюджетные средства ограничены, колониям приходится ориентироваться на внебюджетные каналы финансирования. Основные изменения в исправительной системе в первую очередь коснутся самих осуждённых.
Приказом Минюста России от 9 июня 2005 г. № 85 «Об утверждении норм вещевого довольствия осуждённых и лиц, содержащихся в следственных изоляторах» утверждены нормы вещевого довольствия спецконтингента с учётом применения современных материалов. В ближайшее время ожидаются изменения и в нормах снабжения форменным обмундированием сотрудников пенитенциарной системы. Реализация всех этих направлений возможна при условии не только значительной финансовой поддержки со стороны государства, но и привлечения внебюджетных, в первую очередь собственных источников финансирования, ликвидации заведомо убыточных производств и структур.
Начиная с 1998 г. после принятия Государственной Думой Федерального Собрания Российской Федерации постановления от 21 октября 1998 г. № 3134–11 ГД «О критической ситуации в финансовом обеспечении деятельности пенитенциарной системы в условиях её реформирования» в пенитенциарной системе этому уделяется очень большое внимание. В настоящее время в системе освоено производство основных продуктов питания, вещевого и других видов имущества. Ежегодно при формировании гособоронзаказа первоочередное внимание уделяется внутрисистемным поставкам. На основе заданий оборонного заказа ежегодно формируется программа самообеспечения.
Самообеспечение подразумевает участие в федеральных и региональных целевых программах, централизованные поставки котельно-печ-ного топлива, госконтракты на поставку банно-прачечного оборудования и моющих средств, заказы на поставку лекарственных средств, дезинфекционных камер для лечебно-профилактических учреждений, внутрисистемные поставки казарменной мебели. Развитие внутрисистемного рынка предусматривает самообеспечение пенитенциарной системы продуктами питания, оборудованием продовольственной и медицинской служб, вещевым имуществом, сельхозтехникой, предметами коммунально-бытового назначения.
Сейчас потребности ФСИН России в вещевом имуществе практически полностью удовлетворяются за счёт собственного производства (рис. 28).
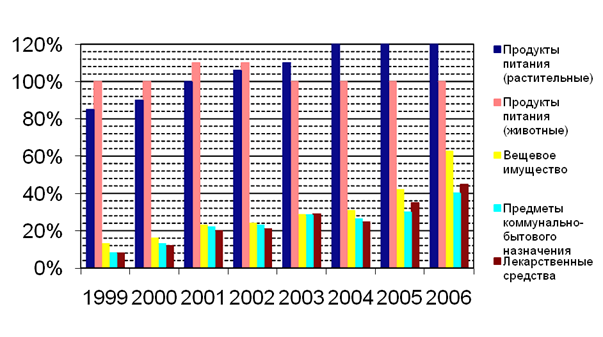
Рис. 28. Обеспеченность пенитенциарной системы
Дата: 2019-12-22, просмотров: 285.
