Проверка эффективности разработанной модели обучения школьному курсу стереометрии на модульной основе осуществлялась с 24 учащимися 10 класса МОУ «Школы №15» города Соликамска в 2007 учебном году. В качестве контрольного класса выступал 10 «А» класс. Внедрение проводилось на уроках геометрии. Целью работы была проверка эффективности разработанной модели обучения школьному курсу стереометрии на основе модульной технологии. Апробирование проводилось в три ступени: констатирующий срез, проведение уроков, контрольный срез. Охарактеризуем каждую ступень. На первой ступени были проведены методики определения уровня обучаемости и обученности (методики представлены в приложении 4) и самостоятельная работа, в ходе которой выявлялись знания и умения учащихся, которыми они обладают на данный момент времени. Вторая ступень работы представляла собой непосредственно уроки. Занятия проводились по схеме:
№ урока-модуля в разделе…
№ урока-модуля в теме…
Тема урока…
Триединая цель урока (темы)…
Дифференцированная цель урока для ученика…
Что должен знать ученик в конце темы…
Что должен уметь ученик в конце темы…
Формируемая область понимания…
Закрепление и развитие общеучебных умений и навыков…
Воспитание на материалах темы…
Тип урока и примененной педагогической технологии…
Вид контроля: самоконтроль, взаимоконтроль, экспертная оценка
Цель первого этапа – проверить уровни обученности и обучаемости (по методикам, указанным в Приложении 2), а также первоначальные уровни сформированности следующих умений и навыков учеников:
1. Владение методами, способами и приемами мыслительной деятельности, а именно умениями:
- анализировать наблюдаемые предметы и явления, выделять в них существенное, главное, отбрасывать второстепенное и находить общее;
- выявлять причинно-следственные связи и отношения объектов, систематизировать факты на новом уровне;
- концентрировать общие положения, отыскивать доказательства, путем абстрагирования и обобщения раскрывать сущность новых понятий;
- видеть проблему и находить несколько способов ее решения с целью выявления наиболее рационального и оригинального;
- ставить цель и определять направления поиска, осуществлять перенос усвоенных знаний и способов деятельности в новые условия и для дальнейшего самообразования;
2. Владение навыками самостоятельного планирования и рациональной организации процесса обучения познавательной деятельности.
3. Наличие познавательной потребности, внутренних установок, побуждающих к самостоятельной деятельности по овладению стереометрией.
Целью второго этапа являлось обучение школьников стереометрии с использованием разработанной модели обучения. На третьем этапе происходила экспериментальная проверка эффективности процесса обучения с использованием разработанной модели обучения.
Первоначально, с учащимися были проведены методики на выявление уровней обученности и обучаемости.
Выявление первоначального уровня сформированности вышеперечисленных умений и навыков происходило следующим образом.
1. Учитель выбирает небольшой по объему новый учебный материал базисного характера на 7-8 минут работы.
Первое следствие аксиом стереометрии.
2. Учитель перед изучением нового повторяет изученный материал, необходимый для усвоения новых знаний.
Сформулируйте аксиомы планиметрии и стереометрии.
3. Учитель объясняет новый материал.
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна. (учащиеся записывают формулировку теоремы).
Дано: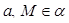 
Доказать: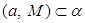 
 |
Доказательство: Заметим, что теорема содержит два утверждения:
1. О существовании плоскости.
2. О единственности плоскости.
а) Рассмотрим прямую а и не лежащую на ней точку М. Докажем, что через прямую а и точку М проходит плоскость. Отметим на прямой а две точки: P и Q. Точки M, P и Q не лежат на одной прямой, поэтому согласно первой аксиоме через эти точки проходит некоторая плоскость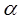 
. Так как 2 точки прямой а (P и Q) лежат в одной плоскости 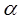, то по второй аксиоме плоскость 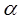проходит через прямую а.
б) Единственность плоскости, проходящей через прямую а и точку М, следует из того, что любая плоскость, проходящая через прямую а и точку М, проходит через точки M, P и Q. Следовательно, эта плоскость совпадает с плоскостью 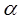, т.к. по первой аксиоме через точки M, P и Q проходит только одна плоскость.
Теорема доказана.
4. Учитель показывает образец применения нового материала в аналогичной и измененной ситуациях.
1. Даны прямые a, b и с, которые пересекают плоскость 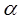в точках М, К и Р. Лежат ли прямые a, b и с в одной плоскости? (Нет, если бы прямые a, b и с лежали в одной плоскости, то точки М, К и Р лежали бы на одной прямой).
2. Дана прямая с – линия пересечения плоскостей 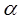и 
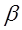. Прямые а и в принадлежат плоскостям 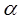и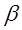 
соответственно. Докажите, что прямые а и в не лежат в одной плоскости. (Предположим, что прямые а и в лежат в одной плоскости. Тогда прямая с также принадлежит этой плоскости. Через прямые а и с можно провести единственную плоскость (плоскость 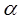), которой будет принадлежать и прямая в. Противоречие.)
5. Учитель проводит самостоятельную работу среди учащихся.
Задания для самостоятельной работы учащихся
1. Напишите, что вы узнали нового.
2. Ответьте на вопрос по содержанию нового материала
Сколько плоскостей может проходить через прямую и точку, не лежащую на ней?
3. Выполните задания по образцу.
Даны прямая и не принадлежащая ей точка. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку, лежат в одной плоскости.
4. Выполните задание в измененной ситуации.
Можно ли через три точки, лежащие на одной прямой, провести две различные плоскости? Объясните ответ.
5. Примените полученные знания в новой ситуации.
В пространстве даны n точек. Сколько прямых можно провести через различные пары этих точек? Сколько плоскостей можно провести через различные тройки этих точек?
Результаты показали, что выполнены все задания у 7 человек, то есть у них третий, очень высокий уровень обучаемости. С четырьмя заданиями справились 9 учеников – у них второй, также высокий уровень обучаемости. Три и менее заданий выполнили 8 учащихся– у них первый уровень.
Степень обученности учащихся (СОУ) рассчитывается по формуле
,
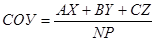По итогам уровневых контрольных работ получен первый уровень преподавания.
В 10 классе у 24 учащихся по 12 предметам: «5» - у 124, «4» - у 119, «3» - у 43, «2» - у 1.
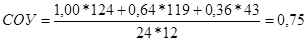, или 75 %.
В программу разработанных уроков входило 10 занятий. На первом уроке был проведен констатирующий срез, в котором содержалось шесть заданий, направленных на выявление знаний по стереометрии.
Все задания среза были направлены на выявление сформированности следующих умений:
- анализировать наблюдаемые предметы и явления, выделять в них существенное, главное, отбрасывать второстепенное и находить общее;
- выявлять причинно-следственные связи и отношения объектов, систематизировать факты на новом уровне;
- концентрировать общие положения, отыскивать доказательства, путем абстрагирования и обобщения раскрывать сущность новых понятий;
- видеть проблему и находить несколько способов ее решения с целью выявления наиболее рационального и оригинального;
- осуществлять перенос усвоенных знаний и способов деятельности в новые условия и для дальнейшего самообразования;
Сформированность названных умений являлась критериями эффективности разработанной методики.
Задания среза представлены в Приложении 3.
Первое задание направлено на выявление сформированности умений анализировать наблюдаемые предметы и явления, выделять в них существенное, главное, отбрасывать второстепенное и находить общее. Второе – на выявление причинно-следственных связей и отношений объектов, систематизацию фактов на новом уровне. Третье задание направлено на то, чтобы видеть проблему и находить несколько способов ее решения с целью выявления наиболее рационального и оригинального. Четвертое – на концентрацию общих положений, отыскание доказательства, путем абстрагирования и обобщения раскрытие сущности новых понятий. Пятое и шестое задания направлены на выявление сформированности осуществлять перенос усвоенных знаний и способов деятельности в новые условия и для дальнейшего самообразования. Констатирующий срез показал, что не все рассматриваемые умения сформированы на данном этапе у школьников:
- с первым заданием полностью справились 15 человек, что составляет 62,5%, частично справились 27%, не справились 10,5%;
- во втором задании у 45% учащихся умение определять точку пересечения прямой и плоскости, двух прямых, а также на нахождение прямой пересечения двух плоскостей сформировано полностью, у 40% это умение сформировано частично, а 15% не справились с заданием;
- с третьим заданием 60% полностью справились, 25% справились частично, 15% не справились;
- с четвертым заданием 25% справились, 30% справились частично, 45% не справились;
- с пятым заданием 68% справились полностью, 15% справились частично, 17% не справились.
- с шестым заданием 65% справились полностью, 13% справились частично, 22% не справились.
Отобразим полученные результаты на диаграмме.
Под термином «умение сформировано полностью» в данном случае понимается выполнение задания с обоснованием и пояснением ответа, а также хода решения. Под «умение сформировано частично» понимается выполнение задания с нечетким пояснением, либо с пропуском некоторых промежуточных рассуждений в ходе решения. Под «умение не сформировано» понимается невыполнение задания. Чаще всего ошибки возникали в заданиях в заданиях четвертого и шестого типа из-за определенной неподготовленности к решению такого типа заданий, а также из-за недостаточно прочного закрепления теоретического материала предыдущей темы.
В ходе выполнения упражнений учащиеся допускали следующие ошибки:
а) неправильно определяли плоскость, которой принадлежит тот или иной объект;
б) неверно указывали точку пересечения некоторых известных элементов, не указывали все точки, принадлежащие плоскости;
в) неправильно указывали прямую пересечения двух плоскостей;
г) не видели логических следствий из ранее изученных теорем или не могли их применить в измененной ситуации;
д) указывали не все требуемые объекты.
Для сравнения результатов констатирующего среза в качестве контрольного класса был взят 10 класс Чердынской общеобразовательной школы. После проведенного аналогичного среза были получены следующие результаты.
- с первым заданием полностью справились 14 человек, что составляет 61%, частично справились 24%, не справились 15%;
- во втором задании у 45% учащихся умение определять точку пересечения прямой и плоскости, двух прямых, а также на нахождение прямой пересечения двух плоскостей сформировано полностью, у 35% это умение сформировано частично, а 20% не справились с заданием;
- с третьим заданием 60% полностью справились, 27% справились частично, 13% не справились;
- с четвертым заданием 32% справились, 34% справились частично, 34% не справились;
- с пятым заданием 65% справились полностью, 20% справились частично, 15% не справились.
- с шестым заданием 60% справились полностью, 20% справились частично, 20% не справились.
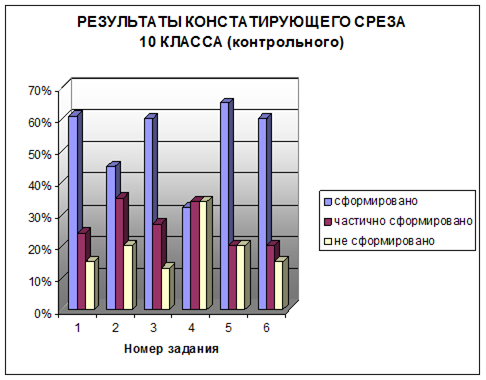
Как показывают полученные данные в контрольном классе результаты оказались практически одинаковыми.
Таким образом, в данном параграфе представлена организация проведения разработанной методики на основе модели с использованием модульной технологии, констатирующий срез, его результаты.
АНАЛИЗ ВНЕДРЕНИЯ МОДЕЛИ
Апробирование методики с использованием разработанной нами модели на основе модульной технологии мы проводили на примере тем: «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей в пространстве» (Приложение 4).
В проведенных уроках использовались следующие формы организации работы учащихся:
- коллективная работа учащихся всего класса;
- работа учащихся в парах.
В процессе работы в парах учащимся предлагался разработанный модуль, изучая который в течение определенного времени, они ознакамливались с теоретическим материалом, искали ответы на поставленные перед ними вопросы. В ходе коллективной работы весь класс отвечал на поставленные вопросы, решал предоставленные им задания.
Процесс обучения происходил с помощью модулей, учебными элементами которых являлись: цель, ознакомление с теоретическими положениями, исторические сведения, проверка усвоения теоретического материала, участие в учебной беседе, самостоятельное выполнение заданий, выполните контрольных заданий. Каждый школьник обучался в индивидуальном темпе по своей программе. Учитель выступал в роли консультанта.
Перечислим методы, используемые в рамках разработанной нами модели (по Ю.К. Бабанскому).
| Методы обучения | |
| Основная подгруппа | Отдельные методы обучения |
| 1. Методы стимулирования и мотивации учения | |
| 1.1. Методы формирования интереса к учению | 1.1. Познавательные игры, учебные дискуссии, методы эмоционального стимулирования |
| 1.2. Методы формирования чувства долга и ответственности в учении | 1.2. методы учебного поощрения, порицания, предъявления учебных требований |
| 2. Методы организации и осуществления учебных действий и операций | |
| 2.1. Перцептивные методы (передачи и восприятия учебной информации посредством чувств): словесные наглядные аудиовизуальные практические | Лекция, рассказ, беседа Иллюстрация, демонстрация Сочетание словесных и наглядных Упражнения |
| 2.2. Логические методы (организация и осуществление логических операций) | Индуктивные, дедуктивные, аналогии и пр. |
| 2.3. Гностические методы (организация и осуществление логических операций) | Проблемно-поисковые (проблемное изложение, эвристический, исследовательский), репродуктивные (инструктаж, иллюстрирование, объяснение и практическая тренировка) |
| 2.4. методы самоуправления учебными действиями | Самостоятельная работа |
| 3. Методы контроля и самоконтроля | |
| 3.1. методы контроля | Устный, письменный, лабораторный и машинный контроль, самоконтроль |
Дадим описание и анализ каждого из проведенных модулей.
Первый модуль посвящен теме «Параллельность прямых и плоскостей в пространстве». Обучаясь по нему учащиеся познакомились с:
- определениями параллельных и скрещивающихся прямых в пространстве, прямой, параллельной плоскости, параллельных плоскостей в пространстве;
- случаями взаимного расположения прямых, прямой и плоскости, а также двух плоскостей в пространстве;
- основными теоремами данной темы;
- способами задания плоскости в пространстве,
- историческими сведениями по теме изучения.
А также закрепили полученные знания на практике путем обсуждения теоретических вопросов в устной беседе, решением заданий, как элементарных, так и повышенного типа.
|
 |
После изучения первого модуля с учащимися проведен промежуточный срез.
1. Каково взаимное расположение прямых KE и MH, если точки K, E, M, H – середины ребер AB, BC, CD, DA тетраэдра ABCD (рис.4)?
| (А) пересекаются | (В) скрещиваются |
| (Б) параллельны | (Г) могут быть пересекающимися, параллельными и скрещивающимися (в зависимости от вида тетраэдра) |
2. Каково взаимное расположение прямых KM и BC? (Рис.4)
| (А) пересекаются | (В) скрещиваются |
| (Б) параллельны | (Г) возможны все три случая (А) – (В) |
3. Каково взаимное расположение прямых AB1 и BD1, если дан прямоугольный параллелепипед ABCDA1B1C1D1? (Рис.5)
| (А) скрещиваются | (В) параллельны | (Д) не определить |
| (Б) пересекаются | (Г) пересекаются или параллельны |
B C
A D
С
A D
Рисунок 5
4. Какие из прямых b = BB1, c = CC1, d = D1C1 скрещиваются с прямой a = AB? (Рис.5)
| (А) только b | (В) только c и d | (Д) все три прямые b, c, d |
| (Б) только c | (Г) только b и c |
5. Каково взаимное расположение прямой B1C1 и плоскости BDA1? (Рис.5)
| (А) параллельны | (В) пересекаются или параллельны |
| (Б) пересекаются | (Г) ответ отличен от (А) – (В) |
6. Каково взаимное расположение плоскостей BDA1 и B1D1C? (Рис.5)
| (А) параллельны | (В) пересекаются или параллельны |
| (Б) пересекаются | (Г) ответ отличен от (А) – (В) |
7. В пространстве даны прямая a и точка M. Сколько существует прямых, проходящих через M и параллельных прямой a?
| (А) 0 | (В) бесконечно много | (Д) 1 или бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
8. Даны параллельные прямая a и плоскость α. Сколько существует плоскостей, проходящих через a и параллельных α?
| (А) 0 | (В) бесконечно много | (Д) бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
9. В пространстве даны две параллельные прямые a и b. Сколько существует плоскостей, проходящих через прямую a и параллельных прямой b?
| (А) 0 | (В) бесконечно много | (Д) 1 или бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
10. Даны две пересекающиеся плоскости α, β и не лежащая на них точка M. Сколько существует прямых, проходящих через M и параллельных плоскостям α и β?
| (А) 0 | (В) бесконечно много | (Д) 0 или бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
11. Даны две скрещивающиеся прямые a и b. Сколько существует пар параллельных плоскостей, одна из которых проходит через a, а другая – через b?
| (А) 0 | (В) бесконечно много | (Д) 0 или бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
12. В пространстве даны две пересекающиеся прямые a, b и не лежащая на них точка M. Сколько существует плоскостей, проходящих через M и параллельных прямым a и b?
| (А) 0 | (В) бесконечно много | (Д) 0 или бесконечно много |
| (Б) 1 | (Г) 0 или 1 |
13. Точки A, B и середина M отрезка AB проектируются в точки A1, B1 и M1. Чему равна длина отрезка MM1, если AA1 = 3 см, B1B = 7 см?
| (А) 5 см | (В) 2 см | (Д) ответ отличен от указанных |
| (Б) 4 см | (Г) 5 см или 2 см |
14. Если два луча, не лежащие на одной прямой, параллельны и лежат в одной полуплоскости относительно некоторой прямой, то они называются …
15. На кубе (рис. 6) укажите прямые, проходящие через т.В и скрещивающиеся с прямой ДС1.
16. На кубе (рис. 6) укажите ребра, параллельные ребру АВ.
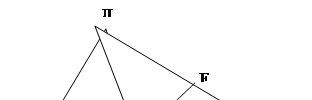
17. Угол между прямыми ДС1 и Д1С равен 90° (рис. 7). Определите, чему равен угол между А1В и ДС1?
18. Угол между прямыми ДЕ и EF равен 60° (рис. 7). Чему равен угол между прямыми ДВ и ВС?
19. Прямые а и в – скрещивающиеся. Известно, что прямая а лежит в плоскости α. Определите, может ли прямая в лежать в плоскости α. объясните почему.
20. Прямые а и в пересекаются. Прямая с является скрещивающейся с прямой а. Могут ли прямые в и с быть параллельными?
Результаты в экспериментальном классе оказались следующие:
- с первым заданием справились полностью 73%, 15% справились частично, 12% не справились;
- со вторым заданием 75% справились полностью, 13% справились частично, 12% не справились;
- с третьим заданием справились полностью 70%, 22% справились частично, 8% не справились;
- с четвертым заданием 73% справились полностью, 18% справились частично, 9% не справились;
- с пятым заданием 72% справились полностью, 16% справились частично, 12% не справились.
- с шестым заданием 76% справились полностью, 16% справились частично, 8% не справились.
- с седьмым заданием 69% справились полностью, 20% справились частично, 11% не справились.
- с восьмым заданием 72% справились полностью, 18% справились частично, 10% не справились.
- с девятым заданием справились полностью 67%, 20% справились частично, 13% не справились;
- с десятым заданием справились полностью 73%, 19% справились частично, 8% не справились;
- с одиннадцатым заданием справились полностью 77%, 14% справились частично, 9% не справились;
- с двенадцатым заданием справились полностью 74%, 21% справились частично, 5% не справились;
- с тринадцатым заданием справились полностью 79%, 15% справились частично, 6% не справились;
- с четырнадцатым заданием справились полностью 71%, 22% справились частично, 7% не справились;
- с пятнадцатым заданием справились полностью 77%, 14% справились частично, 9% не справились;
- с шестнадцатым заданием справились полностью 70%, 16% справились частично, 14% не справились;
- с семнадцатым заданием справились полностью 71%, 18% справились частично, 11% не справились;
- с восемнадцатым заданием справились полностью 73%, 21% справились частично, 6% не справились;
- с девятнадцатым заданием справились полностью 76%, 13% справились частично, 11% не справились;
- с двадцатым заданием справились полностью 80%, 13% справились частично, 7% не справились.
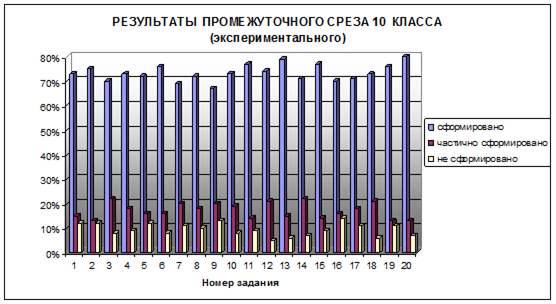
В контрольном классе при проведении аналогичного промежуточного среза результаты получились следующие:
- с первым заданием справились полностью 70%, 12% справились частично, 18% не справились;
- со вторым заданием 70% справились полностью, 11% справились частично, 19% не справились;
- с третьим заданием справились полностью 62%, 25% справились частично, 13% не справились;
- с четвертым заданием 53% справились полностью, 23% справились частично, 24% не справились;
- с пятым заданием 59% справились полностью, 15% справились частично, 26% не справились
- с шестым заданием 62% справились полностью, 19% справились частично, 19% не справились;
- с седьмым заданием 68% справились полностью, 18% справились частично, 14% не справились.
- с восьмым заданием 69% справились полностью, 20% справились частично, 11% не справились.
- с девятым заданием справились полностью 62%, 21% справились частично, 17% не справились;
- с десятым заданием справились полностью 76%, 14% справились частично, 10% не справились;
- с одиннадцатым заданием справились полностью 72%, 12% справились частично, 16% не справились;
- с двенадцатым заданием справились полностью 70%, 20% справились частично, 10% не справились;
- с тринадцатым заданием справились полностью 81%, 10% справились частично, 9% не справились;
- с четырнадцатым заданием справились полностью 75%, 24% справились частично, 11% не справились;
- с пятнадцатым заданием справились полностью 73%, 12% справились частично, 15% не справились;
- с шестнадцатым заданием справились полностью 65%, 21% справились частично, 14% не справились;
- с семнадцатым заданием справились полностью 68%, 15% справились частично, 17% не справились;
- с восемнадцатым заданием справились полностью 70%, 16% справились частично, 14% не справились;
- с девятнадцатым заданием справились полностью 75%, 15% справились частично, 10% не справились;
- с двадцатым заданием справились полностью 76%, 14% справились частично, 10% не справились.
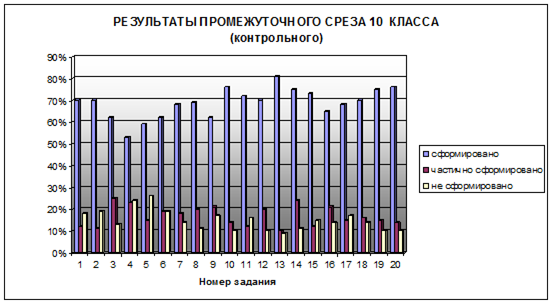
Сравнивая полученные результаты видно, что в экспериментальном классе результаты улучшились благодаря тому, что обучение происходило на основе разработанной модели с использованием модульной технологии.
Структура второго модуля аналогична первому. Он разработан на тему «Перпендикулярность прямых и плоскостей в пространстве». Целью овладения данным модулем является: усвоить понятие угла в пространстве, угла между двумя пересекающимися прямыми в пространстве, перпендикулярных прямых в пространстве, перпендикулярных скрещивающихся прямых, рассмотрение случаев нахождения угла между скрещивающимися прямыми; усвоить понятие прямой, перпендикулярной плоскости, перпендикуляра, высоты пирамиды, прямого цилиндра, рассмотреть признак перпендикулярности прямой и плоскости; усвоить понятие наклонной к плоскости, угла между наклонной и плоскостью, между отрезком и плоскостью; рассмотреть теоремы о трёх перпендикулярах, о перпендикуляре, проведённом из точки к плоскости, об угле между наклонной и плоскостью, научится применять полученные знания при доказательстве определенных фактов и при решении задач практического характера. Обучаясь с помощью данного модуля учащиеся познакомились с:
- определением угла в пространстве, угла между скрещивающимися прямыми, угла между наклонной и плоскостью, угла между соответствующей прямой и плоскостью;
- определением прямой, перпендикулярной плоскости, наклонной к плоскости;
- расстоянием между плоскостью и точкой, между параллельными прямыми;
- понятием общего перпендикуляра;
- основными теоремами данной темы;
Закрепили полученные знания в ходе устной беседы, решая задания на первичное закрепление и в измененной ситуации.
В процессе изучения тем «Параллельность прямых и плоскостей в пространстве» и «Перпендикулярность прямых и плоскостей в пространстве» нам удалось охватить весь объем теоретической информации. Нами были рассмотрены и отработаны задания на отработку основных умений и навыков, которые были сформированы в процессе обучения по данным модулям. При решении упражнений возникшие затруднения сразу устранялись по мере их возникновения и решались подобные задания на закрепление пройденного материала. Они были достаточно интересны, разнообразны и разноуровневы по своему содержанию, отличались новизной формулировок, а также тем, что необходимо было логически мыслить при поиске ответа на поставленный вопрос. Занятия дали положительный результат по формированию следующих умений:
- анализировать наблюдаемые предметы и явления, выделять в них существенное, главное, отбрасывать второстепенное и находить общее;
- выявлять причинно-следственные связи и отношения объектов, систематизировать факты на новом уровне;
- концентрировать общие положения, отыскивать доказательства, путем абстрагирования и обобщения раскрывать сущность новых понятий;
- видеть проблему и находить несколько способов ее решения с целью выявления наиболее рационального и оригинального;
- осуществлять перенос усвоенных знаний и способов деятельности в новые условия и для дальнейшего самообразования;
Для сравнения результатов констатирующего среза по улучшению работы был проведен контрольный срез. Ему посвящен следующий параграф.
Дата: 2019-12-22, просмотров: 238.
