Магнитную силу в случае движения заряженной частицы в магнитном поле исследовал Лоренц. Сила Лоренца
FЛ=q[V,B] (1)
Модуль этого векторного произведения:
FЛ=q×V×Bsin(V,B), (2)
Где q – заряд частицы, V – скорость ее движения, B – индукция магнитного поля.
Проверьте, что размерность В, полученная из соотношения для силы Лоренца совпадает с размерностью, полученной из соотношения для силы Ампера.
Можно провести аналогию между силой Лоренца и силой Ампера, если в определении силы тока J=dq/dt вместо dq записать величину элементарного заряда, а бесконечно малый делитель dt в формуле отнести к dl:
FЛ=dq/dt[dl,B]= dq [dl/dt,B]= q[V,B] =FЛ (3)
(Но (3) нельзя считать доказательным выводом формулы для силы Лоренца из соотношения для силы Ампера. Операция дифференцирования применяется лишь до тех пор, пока величину заряда можно считать непрерывной. Дискретный элементарный заряд нельзя подвергать операции дифференцирования.)
Промышленные токи имеют дело с зарядами, для которых дискретный характер заряда @10-19 Кл не проявляется в эксперименте при вычислении величин.Направление силы Лоренца можно определять по правилу левой руки, по правилу буравчика или по общему правилу определения векторного произведения как и в случае силы Ампера. Таким образом, сила Лоренца всегда перпендикулярна плоскости, в которой лежат вектора магнитной индукции и скорости заряженной частицы (рис. (12)).
 |
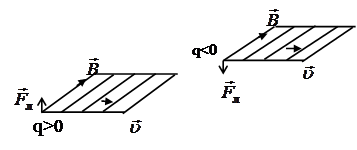Сила Лоренца, будучи всегда направлена перпендикулярно
Рис.10
скорости заряженной частицы, сообщает ей нормальное ускорение, заставляя ее (частицу) двигаться по окружности, и не изменяет модуля ее скорости. Сила, перпендикулярная направлению движения не совершает работы (за счет равенства нулю косинуса в соотношении для силы и работы). Таким образом, сила Лоренца не совершает работы.
Примеры движения частиц в однородном магнитном поле
а) угол a между векторами скорости заряженной частицы V и вектором магнитной индукции В равен 0 или p .
В этом случае сила Лоренца равна нулю за счет равенства нулю синуса в векторном произведении соотношения (2)
FЛ=q×V×Bsin(V,B)= 0.
В отсутствии действующих на частицу сил, она будет двигаться не изменяя скорости (по первому закону Ньютона).
б) угол a между векторами скорости заряженной частицы V и вектором магнитной индукции В равен p /2, то есть V перпендикулярна В. Тогда
FЛ=q×V×B (3)
Частица будет двигаться по окружности в плоскости перпендикулярной вектору В. Поскольку, как мы уже отмечали ранее, сила Лоренца является центростремительной силой. Вспоминая из механики чему равно центростремительное ускорение, запишем:
q×V×B=FЛ=m×aц=m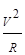 
=q×V×B,
откуда
R =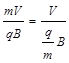 
. (4)
Поскольку поле однородно, (В = сonst), и численное значение скорости не меняется. (Перпендикулярно направленная к ней (к скорости) сила не изменяет модуля скорости.) Поэтому R = сonst. Частица будет двигаться по окружности, плоскость которой перпендикулярна В. Как видно из (4) радиус окружности зависит
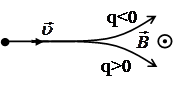
Рис. 14
от отношения заряда частицы к ее массе: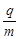 
, эта величина часто встречается в соотношениях физики и носит особое наименование, она называется удельным зарядом частицы.
По характеру отклонения частицы в магнитном поле можно судить о знаке ее заряда. Эксперимент показывает, что для определения направления вращения частицы надо с помощью рис. 13 применить правило левой руки, учитывая, что отрицательная частица
летит против направления тока (поскольку все соотношения электромагнетизма выведены с учетом того, что ток течет в направлении от + к -).
В общем случае период обращения частицы при ее движении по окружности равен длине окружности - 2pR (пройденному частицей пути), поделенному на скорость ее движения - V. В магнитном поле период обращения частицы по окружности с учетом (4) равен:
Т=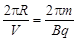 
(5)
Анализируя (5) можно отметить, что период обращения частицы по окружности в магнитном поле не зависит от ее скорости. (Зависимость периода от скорости проявится лишь при стремлении V к скорости света С: V®C).
в) Общий случай движения заряженной частицы в магнитном поле 0< a < p /2 (рис. 14) Одно из проявлений принципа суперпозиции состоит в том, что при анализе движения мы можем разложить вектор скорости на две любые перпендикулярные составляющие и изучать движение вдоль каждого из двух взаимно перпендикулярных направлений независимо друг от друга. Выбор перпендикулярных направлений мы осуществляем наиболее удобным в условиях заданной задачи образом. В нашем случае
 |
Рис. 14
пусть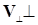 
B и 
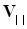
B.
Задача свелась к двум предыдущим задачам: к движению со скоростью параллельной B и движению со скоростью перпендикулярной B, причем
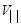=Vcosa , а 
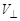=Vsina (6)
Частица движется по окружности, плоскость которой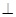 
B со скоростью 
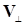. И в то же время она движется поступательно с постоянной скоростью 
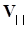в направлении параллельном B.
Таким образом, результирующая траектория заряженной частицы в постоянном магнитном поле представляет собой винтовую линию, ось которой совпадает с одной из силовых линий магнитного поля. (рис. 15). Частица, как бы навинчивается на силовую линию магнитного поля.)
Причем шаг винтовой линии h (см. рис. 14) равен пути, пройденному вдоль винтовой линии, который (путь) равен скорости вдоль этого направления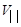 
=Vcosa , помноженной на время, затраченное на прохождение этого пути, которое (время) по определению шага винтовой линии равно как раз периоду обращения частицы вокруг силовой линии: t=T. Учитывая значения скорости (6) и периода (5), получаем:
h=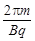 
Vcosa . (11)
Пример решения задачи. Электрон, пройдя ускоряющую разность потенциалов U=1 кВт, влетел в однородное магнитное поле с индукцией В=0,03 Тл под углом a=300 к направлению силовых линий поля. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.
| Рис. 15 |
При решении данной задачи обычно полностью повторяют выводы а), б) и в) данного раздела, так, что раздел 4.1 можно считать решением данной задачи. В условии задачи значения B и a заданы явно, а скорость - V , задана неявно.
Найдем в явном виде скорость и воспользуемся полученными ранее формулами. Пройдя ускоряющую разность потенциалов U, электрон разгоняется и приобретает скорость, которую можно найти из закона сохранения энергии. В подобных задачах предполагают, что в начальный момент времени заряженная частица имела нулевую скорость (эксперимент производимый в современных ускорителях подтверждает уместность такого предположения). Значит, разогнавшись, частица совершит механическую работу, равную изменению ее кинетической энергии
А=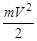 
(1)
(в продолжении подобного эксперимента потенциальная энергия частицы не меняется, поскольку гравитационная сила исчезающе мала по сравнению с магнитной). Эта работа А совершается силами электрического поля. По определению разности потенциалов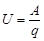 
, где q – заряд частицы. В случае электрона заряд q равен заряду электрона, который обозначается символом e. Таким образом с другой стороны та же самая работа равна
А= Ue. (2)
Объединяя (1) и (2), получаем:
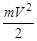= Ue ,
откуда
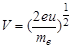, (3)
где me – масса электрона.
Используя полученные ранее формулы (7) и (11), подставляя в них найденное значение V, получаем:
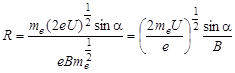(4)
h= 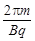Vcosa = 
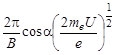(5)
Проверим размерности полученных величин:
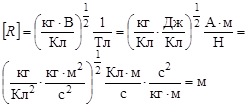
Пояснение вывода размерности: в первом равенстве мы поименовали размерности входящих в (4) величин; во втором равенстве мы выразили размерность разности потенциалов - (U), (Вольт, В) из определения разности потенциалов U = A / q, где размерность работы – А, это Джоуль (Дж), а размерность электрического заряда – q, это Кулон (Кл). А также во втором равенстве мы выразили размерность В - магнитной индукции – Тл, через соотношение силы Ампера (как на с. 28 этого методического пособия); в последнем равенстве мы расписали (Дж) через определение работы, (Н) через второй закон Ньютона (который представляет собой определение силы) и упростили выражение, сократив одинаковые размерности.
Чтобы понять особенности вывода размерности шага винтовой линии, достаточно изучить данное абзацем выше пояснение, поскольку «шаг» зависит от тех же физических величин, что и радиус, следовательно, и расшифровки размерностей будут такие же.
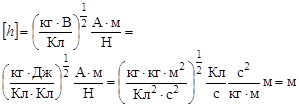
Вычислим числовые значения величин:
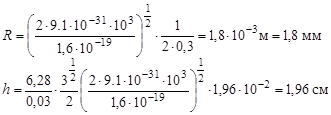
Задача решена.
Ответ: Радиус винтовой линии равен 1,8 мм, а шаг равен 1,96 см.
§5 Электромагнитная индукция 5.1. Закон электромагнитной индукции
Запишем полученное ранее соотношение (20, § 3) для работы, совершаемой магнитными силами при движении замкнутого контура в магнитном поле.
dA = JdФ (1)
По закону сохранения энергии эта работа должна быть на что-то затрачена. Она (работа) в этом случае может быть затрачена лишь на выделение тепла в контуре. Можно предположить, что это тепло Джоулево, т.е. разогрев проводника произойдет под действием направленного движения заряженных частиц, т.е. по проводнику потечет ток.
Джоулево тепло подсчитывается по формуле –
dQ = UJdt.
Приравнивая теплоту работе магнитной силы, получим:
UJdt = JdФ. (2)
Поделив правую и левую части (2) на Jdt, получим
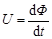. (3)
Согласно (3) можно предположить, что в замкнутом контуре, помещенном в магнитное поле при изменении во времени потока магнитной индукции в нем (в контуре) может возникать ЭДС индукции равная по величине dФ/dt, которая вызывает (в контуре) падение напряжения равное U.
Фарадей обнаружил это явление экспериментально (1831 г.). В замкнутом контуре, помещенном в магнитное поле при изменении потока магнитной индукции пронизывающего этот контур возникает ЭДС магнитной индукции x, равная
x= -dФ/dt (3)
Знак (-) в (3) означает тот экспериментальный факт, что возникающая ЭДС производит индукционный ток, препятствующий изменению потока (правило Ленца). Правило Ленца соответствует условию выполнения закона сохранения энергии. Можно убедиться на конкретных примерах, что иначе закон сохранения энергии не выполнилось бы.
Рис. 15 иллюстрирует как при увеличении магнитного потока Ф=(В,dS) через контур возникающий ток уменьшает значение модуля В в пространстве плоскости контура (рис. 15, а) и увеличивает при уменьшении Ф.
Эксперимент Фарадея показал, что возникающая ЭДС не зависит от способа, которым изменяют поток через поверхность, «натянутую» на контур. Магнитный поток может меняться, благодаря изменению формы контура и его расположения в магнитном поле, а также вследствие изменения во времени индукции В.
Если закон изменения Ф(t) не известен в общем виде в каждый момент времени, то рассчитывают среднее значение ЭДС индукции для моментов времени в которые Ф(t) известны
<x>=(Ф2-Ф1)/(t2- t1) (4)
Если контур, в котором индуцируется ЭДС, состоит из N витков (как, например, в случае соленоида), то индуцируемая ЭДС будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности
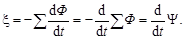(5)
 |
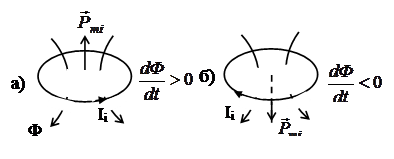Рис. 15
Величина Y=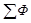 
называется потокосцеплением или полным магнитным потоком. Если магнитный поток через каждый виток соленоида одинаков, то
Y=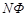 
. (6)
Поскольку числовая константа N – безразмерна, то размерность потокосцепления такая же, как у потока -
[Y]=[Ф]=Вб.
Дата: 2019-12-10, просмотров: 281.
