Вернемся к соотношению (3, §2), перенумеруем его в новом параграфе:

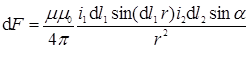.                   (1)

Био, Савар и Лаплас введя соотношение для вектора магнитной индукции B, переписали (1) для нахождения модуля силы так:

dF=idlBsina,                                   (2)

где a - угол между элементарным отрезком с учетом направления силы тока в нем и направлением вектора магнитной индукции.

И в векторной форме

dF=[idl,В].                                   (3)

Соотношение (3) учитывает все случаи возникновения магнитной силы при любом возможном взаимном расположении проводников.

Сила, действующая на проводник с током в магнитном поле в честь ученого исследовавшего связанные с ней (силой) проблемы названа силой Ампера. Для определения направления силы Ампера в случае, когда проводник перпендикулярен направлению силовых линий магнитного поля, удобнее, чем общим правилом определения направления векторного произведения, пользоваться правилом левой руки:

Если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца указывали направление тока, то оттопыренный большой палец укажет направление магнитной силы, действующей на элемент проводника. Если проводник прямолинейный, то все силы, действующие на его элементарные участки, окажутся направленными в одну сторону. И суммарная сила будет равна:

F= 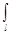idlB(l)sina.                        (4)

Если магнитное поле однородно (т.е. величина и направление вектора магнитной индукции постоянны в некоторой области пространства, в которую наш проводник целиком входит в процессе своего движения), то мы приходим к соотношению для силы Ампера, известному из средней школы:

                                                 F=ilBsina,                                (5)

при a=90⁰, (см. рис. 6)

F=ilB .                                              (6)

Размерность магнитной индукции определяется из соотношения (5) и носит особое название Тл= .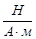

F= 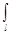dF.               (7)

Если проводник не прямолинеен, а, например, имеет вид, приведенный на                                    

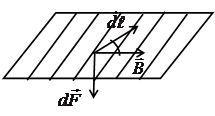
      Рис.6                      рис. 7, то, разбив весь проводник на элементарные участки dl, результирующую силу необходимо искать, суммируя геометрически все элементарные силы dF, действующие со стороны магнитного поля на отдельные участки проводника.

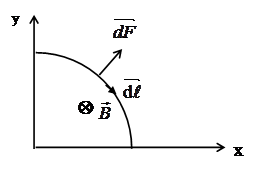В случае плоского контура (рис. 7) все элементарные силы dF лежат в одной плоскости, но при переходе от одного элемента dl проводника к другому, направление силы меняется. Поэтому, для нахождения результирующей силы, сначала следует отдельно искать ее проекции на две произвольные де-                   

           Рис.7                                  картовы оси координат (выбирают наиболее удобную в условиях конкретной задачи декартову систему), а затем искать результирующую силу по правилу векторного сложения (в частности это можно сделать с помощью теоремы Пифагора):

 F_х= 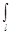 dF_х ,  F_у=  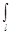dF_у , F=( F²_х+ F²_у)^1/2.          (8)

Соотношения (4-8) необходимо использовать с некоторой осторожностью. Они (эти соотношения) получены для случая достаточно жестких проводников, движущихся поступательно, когда каждую силу, приложенную к участку dl можно перенести в центр масс.