а) работа, совершаемая при перемещении проводника с током в однородном магнитном поле

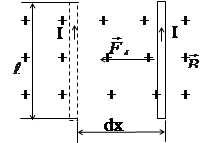
Пусть отрезок прямолинейного проводника длиной l, по которому течет ток J, переместился в однородном магнитном поле с индукцией B на расстояние dx в направлении, перпендикулярном силовым линиям поля, вдоль линии действия силы Ампера (рис. (10). Магнитная сила (сила Ампера) совершит при этом работу

dA=Fdxcos0⁰=Fdx=JBlsin90⁰dx = JBldx . Так как ldx = S, получим dA=JBdS = JdФ.

dA = JdФ           (18)

 (Выражение (18) справедливо и в общем случае относительного расположения проводника и поля, но доказательство этого выражения для общего случая достаточно громоздко, хотя не представляет принципиальной сложности и может быть прове

                                                   дено студентом самостоятельно        

                                                    в качестве задачи). При равно-    

             Рис. 11                     мерном движении про -

водника для конечного перемещения Dх можно записать

                                            A = JDФ                                      (19)

DФ – магнитный поток сквозь поверхность прочерчиваемую проводником в процессе его равномерного движения.

 б) работа, совершаемая при перемещении в магнитном поле замкнутого контура с током

Получим выражение искомой работы так же, как впредыдущем разделе, для частного случая.

В случае осуществления условий движения, показанного на рис. 9 отрезки проводников с током – стороны b не совершают работы (движение происходит перпендикулярно к линии действия силы и угол а=90⁰, в выражении для работы dA=Fdxcosа превращает значение cosa в 0.) Отрезки а совершают работу, которую можно вычислить в соответствии с соотношением (17), причем работа проводника а будет положительной, а проводника b - отрицательной (косинус угла 180⁰ между линией действия магнитной силы и перемещением Dх равен –1). Суммарная работа контура

                               А= J (Ф₁-Ф₂).

В однородном магнитном Ф₁=Ф₂ поле DФ=Ф₁-Ф₂=0, DФ ¹0 лишь в том случае, когда происходит изменение собственного потока, пронизывающего контур проводника. Таким образом, замкнутый контур в магнитном поле может совершать работу лишь в том случае, когда изменяется поток, пронизывающий этот контур. Cоотношения (18) и (20), совпадая по внешней форме, имеют глубоко различный физический смысл.

dА= JdФ                                                 (20)

Как показал эксперимент Фарадея, соотношение (20) останется в силе при любом способе изменения величины потока магнитной индукции. В следующем разделе рассмотрим пример вращения замкнутого контура с током в однородном магнитном поле.

б) работа, совершаемая при повороте замкнутого контура с током в однородном магнитном поле

Из курса механики известно, что

,

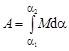здесь M – вращающий момент сил, действующий на контур с током, a - угол поворота контура; поворот осуществляется от угла a₁ до a₂. В разделе 3.3 мы убедились в том, что           

M=[P_m,B].

Подставляя значение момента сил и расшифровывая значение магнитного момента, производим несложное интегрирование (попытайтесь сделать это сами, прежде, чем прочтете следующий пример решения задачи) и получаем     

                               А= J(Ф₂-Ф₁),                                 (21)

как и было «обещано» в предыдущем разделе.

Пример решения задачи. Плоский квадратный контур со стороной а=20 см, по которому течет ток J=100 А, свободно устанавливается в однородном магнитном поле (В=0,1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси ОО`, проходящей через середины его противоположных сторон, на угол b=60⁰. (При повороте контура сила тока в нем неизменна.)

Дано: a=0,2 м В=0,1 Тл J= 100 A b=600 Найти: А

Решение Итак, 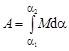,         (1) здесь M – вращающий момент, действующий на контур с током, a - угол

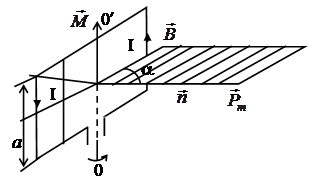
Рис.12

поворота контура; поворот осуществляется от угла a₁ до a₂. В разделе 3.3 мы убедились, что M=[P_m,B], или в скалярном виде

                                       M=JSBsina                                        (2)

(напомню, что P_m=JSn). По условию задачи контур свободно установился в магнитном поле. Это условие означает что момент сил, действующий на рамку равен нулю, это возможно, когда a=0 (см рис. 11), т.е. когда векторы P_m и B совпадают по направлению. При повороте рамки именно этот угол a и будет меняться в соотношении (1) от            

                                 a₁=0 до a₂=60⁰                                        (3)

В случае этой задачи             

                                   S=а².                                            (4)

Подставляя (4) в (2), (2) в (1), учитывая пределы интегрирования в соответствии с (3), получаем

                   ,

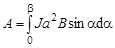откуда

А= Ja²B(-1)(cos0–-cos60⁰)=

= J(Ф₂Ф₁)= 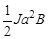=1/2×100×0,04×0,1=0,2Дж.                            (5)

Заметим, что выражение, полученное в (5) представляет собой произведение тока J на скалярное произведение вектора магнитной индукции B и вектора-площадки S. (Что по определению представляет собой поток вектора магнитной индукции; проверьте, что угол, косинус которого стоит в формуле, соответствует углу скалярного произведения двух этих векторов.) Задачу можно было бы решить проще, сразу используя соотношение (5), но мы еще раз на этом примере убедились в справедливости завершающего вывода предыдущего раздела.

Проверим размерность:

[A]=A×м²×Тл, размерность физической величины В – Тл, (как и любой другой) восстанавливаем с помощью соотношения, в котором она впервые появляется. Для физической величины – магнитной индукции это выражение для силы Ампера:

                               dF=[Jdl,B],

откуда

Тл= 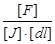= 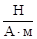. [A]=A×м²× 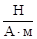=Н×м=Дж.

Получили размерность работы Дж.