Действие магнитного поля на замкнутые проводники с током представляет большой интерес, так как на этом физическом явлении основаны все современные электрические двигатели. Рассчитаем величину момента магнитных сил M, поворачивающего прямоугольную рамку в однородном магнитном поле.

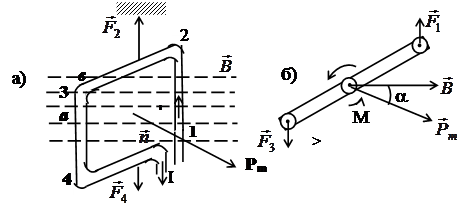
Рассмотрим (рис. 9) проводник, изогнутый в виде прямоугольной рамки, помещенный в однородное магнитное поле с постоянной по величине и направлению в каждой точке пространства индукцией B . (Пусть этот проводник (он же рамка) свободно подвешен на неупругой нити). В отсутствии тока он (проводник-рамка) находится в положении безразличного равновесия.

 В процессе вывода соотношения для момента магнитной силы (как и многих других соотношений электромагнетизма) можно убедиться в том, что удобно ввести новую характеристику магнитного поля – магнитный момент контура с током - P_m. В случае плоского контура

P_m=JSn ,                                      (10)

где J – ток в контуре, S – площадь контура, n – орт (орт это единичный вектор) положительной нормали. (Нормаль считается положительной, когда из конца вектора P_m, направление которого совпадает с направлением n (в силу равенства (10)), ток в контуре виден текущим против часовой стрелки).Удобство введения физической величины – вектора магнитного момента P_m состоит в том, что произведение JSn достаточно часто встречается в физических законах электромагнетизма. Размерность магнитного момента определяется из (10) [P_m]=A×м².

При пропускании через рамку постоянного тока, силы магнитного поля стремятся повернуть ее (рамку) таким образом, чтобы ее собственный магнитный момент совпал с направлением вектора индукции магнитного поля B. (О направлении силовых линий магнитного поля как раз и можно судить по ориентации в этом поле рамки с током. Плоскость рамки устанавливается перпендикулярно направлению B, причем из конца этого вектора ток в рамке виден идущим против часовой стрелки.) Возникает момент магнитных сил, действующих в однородном магнитном поле на прямоугольную рамку. Разберемся каким образом он (момент магнитных сил) возникает и рассчитаем его.

Обозначим стороны, которые лежат в плоскостях параллельных B, буквой b, а стороны, перпендикулярные B, буквой a. Силы F₁ и F₃, действующие на прямолинейные проводники 1-2 и 3-4, направлены перпендикулярно плоскости рисунка в противоположные стороны, но не вдоль одной линии действия, поэтому эти силы создают крутящий момент. (На рисунке 9, б показан вид рамки сверху). По закону Ампера обе эти силы численно равны величине, модуль которой рассчитывается с помощью соотношения (6) (проверьте, что в нашей задаче выполнены условия реализации соотношения (6))

F₁ = F₃=JaB                                                (11)

Силы F₂ и F₄, приложены к проводникам 2-3 и 4-3, направлены вдоль одной прямой (вдоль оси рамки), уравновешивают друг друга

Рис.9

F₄= JbBsin (90-a)) и крутящего момента не создают.

Результирующий вращающий момент M, действующий на рамку, равен моменту пары сил F₁ = -F₃, который рассчитывается так:                                 M= [F₁,l].                                        (12)

По модулю плечо момента сил l=bsina. Подставляя в (12) значение плеча и силы, получаем:

M=JaB bsina= JabBsina= JSB sina=P_mBsin(P_mB)        (13)

Таким образом, по определению векторного произведения модуль момента сил рассчитывается как векторное произведение двух векторов P_m и B .

Определим порядок этих векторов в векторном произведении. (Векторное произведение некоммутативно, т.е. от порядка записи векторов зависит его знак, который (знак) соответствует направлению их произведения вдоль оси перпендикулярной пло-скости, в которой лежат эти вектора в ту или другую сторону).

Вращение рамки под действием пары сил F₁ и F₃ происходит вокруг вертикальной оси, перпендикулярной P_m и B (рис 9, б). Вектор вращающего момента M направлен вдоль оси вращения так, что из его конца вращение рамки под действием пары сил F₁ и F₃ видно происходящим против часовой стрелки (на рис. 4, б вектор M направлен перпендикулярно плоскости чертежа к нам. Чтобы убедиться в этом, повторите правило определения направления вектора момента сил, изученное в механике). Исходя из общего правила определения направления векторного произведения, чтобы направление М было верным, необходимо рассчитывать его так:     M=[ P_m, B].                           (14)