Общий принцип суперпозиции работает и для сил магнитного поля. Эксперимент показывает, что индукция поля магнитной силы в некоторой точке пространства равна геометрической сумме векторов индукции, созданных в этой точке всеми отдельными отрезками проводников с током, образующими исследуемый контур.
Если нам известны величины и направления векторов магнитной индукции от каждого из отрезков, образующих контур, то
B= B1+ B2+ … + Bi+ …. Bn (7)
результирующее значение вектора индукции в некоторой точке равно векторной сумме индукций, создаваемых в этой точке отдельными отрезками контуров с током. В частности, когда длины отрезков контуров берутся бесконечно малыми, то

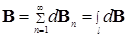 (8)
(8)
Часто контуры оказываются такими, что направления векторов dB от каждого Jdl одинаковыми и мы находим интегральную сумму модулей элементарных индукций:

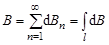 (9).
(9).
2.4. Нахождение числовых значений В и Н - силовых характеристик магнитных полей токов, текущих по проводникам правильной геометрической формы
Применим соотношения (4), (6), (8) и (9) для расчета силовых характеристик полей, создаваемых контурами проводников ничтожно малого сечения: а) кругового проводника с током, б) прямолинейным отрезком проводника с током конечной длины и в) бесконечно длинным проводником с током. Вывод соотношений а), б), в) можно рассматривать, как примеры решения задач.
а) Найти вектор индукции магнитного поля – В, кругового проводника радиуса R , обтекаемого током J на его оси (рис. 1).
Разобьем проводник с током на бесконечно малые отрезки dl. Можно проверить, что для всех отрезков dl индукция, создаваемая протекающими в них токами, направлена вдоль образующей конуса, имеющего линейный угол при вершине, такой, что a/R=tgb (рис.1).
(Вспомните, что векторное произведение двух векторов перпендикулярно плоскости, в которой лежат эти вектора.) Для того, чтобы выяснить в какую сторону вдоль этого перпендикуляра направлен вектор магнитной индукции, удобнее (удобнее чем общим правилом определения направления векторного произведения ) воспользоваться правилом буравчика. Далее, закручиваем правый винт (буравчик) ориентированный вдоль тока так, чтобы конец его ручки в первый момент движения совпал с точкой А. В какую сторону начнет двигаться ручка буравчика в первый момент движения, в ту же сторону вдоль перпендикуляра к плоскости векторов r и dl и направлен искомый вектор.)
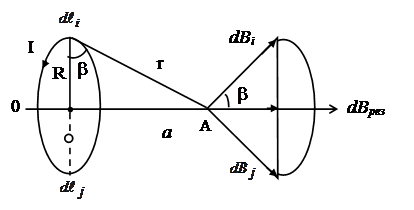 |
Рис. 1
На рис. 1 вектор магнитной индукции направлен от витка. Не трудно проверить, что если бы ток шел в другую сторону, то вектор магнитной индукции был бы направлен к витку. Определив направления векторов всех элементарных индукций dB, найдем направление и модуль суммарного вектора B.
Из условий однородности материала витка, постоянства тока и высокой симметрии геометрии задачи, очевидно, что для каждого dBi, созданного элементом dli, найдется симметрично расположенный элемент dlj, такой, что созданная им магнитная индукция dBj в сумме с dBi даст вектор, направленный вдоль оси (см. рис. 1).
В аналитической геометрии доказана теорема о том, что если известно направление результирующего вектора – суммы нескольких векторов, то эта результирующая сумма равна сумме проекций всех слагаемых на это направление. Воспользовавшись этой теоремой, замечаем, что проекция каждого из слагаемых dBi равна
B= 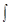 dBi=
dBi= 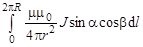 . (10)
. (10)
Как видно из рис. 1, sina=1 (угол между касательной к окружности и направлением на точку А для каждого dl равен 900), Cosb=R/(R2+a2)1/2, r 2= R2+a2. Подставляя соответственные значения величин в (9), получим,
B = 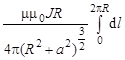 .
.
И, наконец, взяв интеграл, придем к окончательному выражению для индукции кругового тока на его оси:
B = 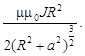 (11)
(11)
В центре кругового тока, когда a=0, получим соотношение
B= 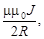 соответственно (см. 6) H=
соответственно (см. 6) H= 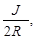 (12)
(12)
Направление вектора B показано на рисунке.
Задача решена.
б) Нахождение магнитного поля прямолинейного проводника конечной длины, обтекаемого током J (рис. 2)
Для проводника известной длины относительно любой точки А вблизи него нетрудно измерить величины r0, a1 a2, будем считать эти величины заданными. Все элементы Jdli и ri лежат в одной плоскости, которая образована отрезком l с током I – и радиусом-вектором, r0. Для того, чтобы определить в какую сторону вдоль перпендикуляра к этой плоскости направлен вектор магнитной индукции – к нам или от нас, воспользуемся правилом буравчика (см. с. 9).
На рис. 2 вектор магнитной индукции направлен от нас за чертеж, такое положение вектора мы будем отмечать на чертеже кружком с перекрестием внутри расположенным рядом с вектором - + B. Не трудно проверить, если бы ток шел в другую сторону, то вектор магнитной индукции был бы направлен к нам, мы пометили бы его на чертеже кружком с точкой внутри – · B.
Определив направление вектора, найдем его модуль. В предыдущих параграфах было рассмотрено соотношение для расчета магнитной индукции, создаваемой бесконечно малым отрезком проводника. Воспользовавшись соотношением (9). (Направления dBi от каждого элемента dl одинаковы. Проверьте по правилу буравчика!).
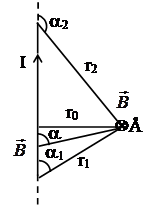
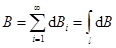 ,
,
вычислим модуль В, подставляя значение dB из (4)
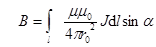 . (13)
. (13)
С помощью рисунка 2, пользуясь теоремами элементарной геометрии, можно выразить величины r и dl через ro и тригонометрические функции переменного угла a. После этого взяв интеграл (10) в пределах от a1 до a2, получим модуль
индукции в точке А вблизи прямоли-
Рис. 2 нейного проводника с током[1].
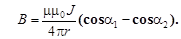 (14)
(14)
Воспользовавшись соотношением связи между индукцией и напряженностью магнитного поля (6), получим –
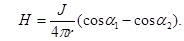 (15)
(15)
в) для случая бесконечно длинного проводника a1=0, a2=1800. Cosa1=1, Cosa2=-1 из (14-15) получим:
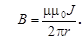 (16)
(16)
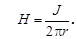 (17)
(17)
Размерность Н можно определить с помощью (17): [Н] = 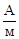 .
.
Направлен вектор перпендикулярно чертежу за чертеж, как показано на рис. 2.
Задача решена.
г) Нахождение магнитного поля соленоида. Нетрудно показать (см., например, [1-4]), что магнитное поле многовитковой катушки длиной l в случае, когда l>>d (d – диаметр катушки), имеет напряженность
Н= Jn , (14)
где n число витков, приходящихся на единицу длины. [n]=м-1 Такая катушка называется соленоидом. Поле внутри соленоида однородно. «Однородно» - означает одинаково по модулю и направлению в любой точке внутри соленоида. Направлен вектор B вдоль оси соленоида в соответствии с правилом буравчика, примененного к любому из его витков.
Задача решена.
Примеры решения задач на нахождение индукции магнитного поля, создаваемой различными контурами с током:
Общие замечания. Все соотношения для расчета индукции магнитных полей, создаваемых конечными и бесконечно длинными проводниками, круговыми контурами и соленоидом мы получили с помощью принципа суперпозиции (т.е. геометрическим суммированием индукции от каждого бесконечно малого участка контура).
Принцип суперпозиции применяется и по отношению к конечным участкам контуров. А именно, если сложный контур может быть условно разделен на элементы, представляющие собой прямолинейные участки и части окружности, то суммарная индукция находится как векторная сумма индукций. Каждое слагаемое в этой сумме рассчитывается по известной формуле (соответственно для отрезка (14), для окружности (13) и т.д.)
Пример 1. Два параллельных длинных проводника, по которым текут в одном направлении одинаковые токи i1 = i2 =60 А, расположены на расстоянии d=10 см друг от друга. Определить магнитную индукцию B поля, создаваемого этими проводниками в точке С, отстоящей от одного проводника на расстоянии r1=5 см, от другого – на расстоянии r2=12см.
Дано: J1=J2=60 A d=10см=0,1м r1=5см=0,05 м r2=12см=0,12 м m0=4p×10-7Гн/м
Найти: B=?
| Решение Пользуясь теоремами элементарной геометрии, нетрудно доказать, что точка С лежит в плоскости перпендикулярной к каждому из проводников. Доопределим задачу. Будем считать, что имеем дело с проводниками бесконечной длины и исчезающе малого сечения. Каждый |
из таких проводников создает индукцию, модуль которой находится из соотношения (16). Направление индукции от каждого проводника идет вдоль перпендикуляра, восстановленного в точке C к плоскости, образованной проводником и перпендикуляром, опущенным из точки С на прямолинейный проводник. Направление вектора индукции вдоль этого перпендикуляра определяется по правилу буравчика. (Правило буравчика с. 9). Тогда при решении задачи можно применить принцип суперпозиции, складывая векторно два значения индукции, создаваемой каждым из проводников в отдельности. См. рис. 3. В1 создает проводник D; B2 – A.
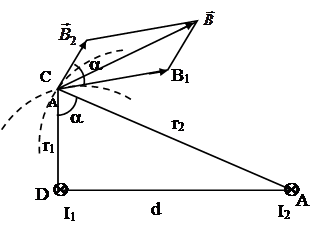 Итак, из соотношения (16) модуль каждого из векторов находим следующим образом:
Итак, из соотношения (16) модуль каждого из векторов находим следующим образом:
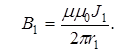
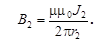
(1)
Если в задаче специально не оговорена среда, считается, что дело происходит в Рис. 3 воздухе, где
mвоздуха=1. Абсолютное значение модуля суммарной магнитной индукции B может быть найдено, например, из теоремы косинусов
B=(B12+B22+2B1B2cosa)1/2, (2)
Подставляя в (2) соотношения (1), получим:
B= 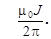 (r1-2+r2-2+2r1-1r2 -1cosa)1/2, (3)
(r1-2+r2-2+2r1-1r2 -1cosa)1/2, (3)
Из рисунка видно, что a=1800-ÐДАС; ÐДАС =b. По теореме косинусов запишем:
d2= r12+r22-2r1r2cosb, откуда
cosb=(r12+r22-d2)/(2r1r2) и (3) преобразуется так:
B= 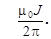 (r1-2+r2-2-2r1-1r2 -1cosb)1/2, (4)
(r1-2+r2-2-2r1-1r2 -1cosb)1/2, (4)
Подставляя числовые значения, получим:
cosb= 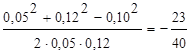 .
. 
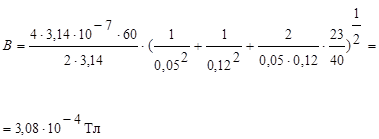
[B]= 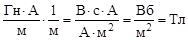 . Расшифровку размерности Гн мы проведем в пятом параграфе (см. с. 38). Итак, модуль В найден, направлен вектор В, как показано на рис. 3.
. Расшифровку размерности Гн мы проведем в пятом параграфе (см. с. 38). Итак, модуль В найден, направлен вектор В, как показано на рис. 3.
Ответ: численное значение индукции B=0,308мТл, а направление В определяется правилом сложения векторов и показано на рисунке 3.
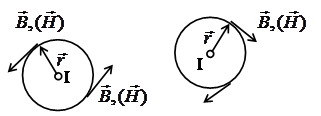 |
Общие замечания. Если контур с током плоский, то направление индукции от каждого элемента этого контура одно и то же. Действительно, с помощью правила буравчика можно проверить, что вектор магнитной индукции В вблизи отрезка прямого проводника с током в каждой точке окружности, которая лежит в плоскости перпендикулярной проводнику, а центр которой (окружности) находится на прямой, направлен (вектор В) каждый раз по касательной к этой окружности (см. рис. 4 а). Линия, в каждой точке которой вектор магнитной индукции направлен по касательной к ней, называется силовой линией магнитного поля.
| а) ток направлен перпендикулярно плоскости чертежа к нам | б) ток направлен перпендикулярно плоскости чертежа от нас Рис.4 |
Значит окружности, лежащие в плоскостях, перпендикулярных к проводнику с током, центры которых лежат на этом проводнике являются силовыми линиями магнитного поля, создаваемого им (отрезком с током). С помощью элементарной геометрии нетрудно доказать, что для любой заданной точки плоскости перпендикулярной обоим проводникам, окружности силовых линий от каждого провода соприкасаются в этой точке (рис. 4), и касательные векторы Вi к каждой из окружностей складываются алгебраически.
Путем аналогичных рассуждений можно убедиться, что от кругового плоского контура в заданной точке индукция направлена также, как от прямолинейного отрезка. Общность направления индукции от каждого элемента плоского контура можно проверять для каждой конкретной задачи (пока не привыкнешь к тому, что это в самом деле всегда так, а не иначе).
Задачи часто подбираются так, чтобы искомая точка, в которой определяется В, являлась центром окружности круговой части контура. Поэтому при решении задач для каждого элемента плоского контура мы часто будем пользоваться формулами (11, 12, 15, и 16).
Из принципа суперпозиции следует, что если нам дана часть кругового контура, в центре которой определяется индукция, (например, половина окружности, или четверть, то прежде, чем суммировать индукцию от круговой части контура, соотношение (11) надо будет помножить соответственно на 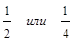 .
.
Пример 2. По контуру в виде равностороннего треугольника идет ток J=40 А. Сторона треугольника а=30 см. Определить индукцию магнитного поля в точке пересечения высот.
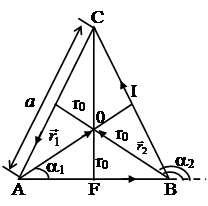
| Дано: J=40 A а=30 см =0,3 м m0=4p×10-7 Гн/м В - ? | Решение Расположим треугольный виток в плоскости чертежа, и зададим направление тока в нем (рис. 5). Согласно принципу суперпозиции магнитных полей, магнитная индукция |
 поля треугольного витка будет равна геометрической сумме магнитных индукцией, создаваемых каждой стороной в отдельности
поля треугольного витка будет равна геометрической сумме магнитных индукцией, создаваемых каждой стороной в отдельности
В=В1+В2+В3 (1)
При заданном направлении тока в точке О пересечения высот треугольника все векторы индукции, а значит и искомый результирующий вектор будут направлены перпендикулярно плоскости чертежа «к нам». (Проверьте, применив правило буравчика, с. 9).
Рис.5 Кроме того, из соображения симметрии следует, что абсолютные значения этих векторов будут одинаковы, т.е. В1=В2=В3, тогда абсолютное значение результирующего вектора
В=3В1. (2)
Магнитная индукция В1 поля, создаваемая отрезком прямолинейного проводника с током, выражается формулой (14)
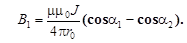 (3)
(3)
где в соответствии с условиями вывода формулы (14) a1 и a2 – углы между радиус-векторами r1 и r2, соединяющими концы этого отрезка с точкой, в которой исследуется поле и направлением тока в этом проводнике; r0 – кратчайшее расстояние от исследуемой точки до проводника (рис. 5).
Учитывая, что для отрезка равностороннего треугольника - проводника АВ, высота является биссектрисой
a1= 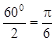 , a2 =
, a2 = 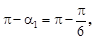 следовательно,
следовательно, 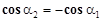 и соотношение (3) можно переписать в виде
и соотношение (3) можно переписать в виде

Подставив это выражение в формулу (2), найдем:
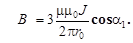
Используя теоремы равностороннего треугольника о том, что все высоты в нем являются одновременно биссектрисами и медианами, а в точке пересечения делятся в соотношении 1:3 -r0= 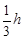 , где h – высота. Из прямоугольных треугольников DCB и DOB найдем h =(а2-а2/4)1/2=
, где h – высота. Из прямоугольных треугольников DCB и DOB найдем h =(а2-а2/4)1/2= 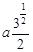 , r0=
, r0= 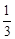
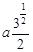 . Подставляя значение r0 в последнее соотношение для В и учитывая, что если в задаче не оговорена среда, в которую помещен проводник, то m=1, получим
. Подставляя значение r0 в последнее соотношение для В и учитывая, что если в задаче не оговорена среда, в которую помещен проводник, то m=1, получим
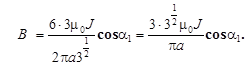
Проверим размерность В:
[B]= 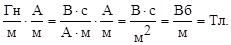 (Расшифровка размерности – Гн, будет произведена в §5, с 38 при исследовании явления самоиндукции.) Подставляя численные значения величин, получаем:
(Расшифровка размерности – Гн, будет произведена в §5, с 38 при исследовании явления самоиндукции.) Подставляя численные значения величин, получаем:
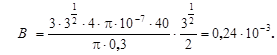 Итак модуль и направление вектора В найдены.
Итак модуль и направление вектора В найдены.
Ответ. B=0,24×10-3Тл=0,24 мТл. Направление вектора магнитной индукции перпендикулярно плоскости чертежа и обращено к нам.
Дата: 2019-12-10, просмотров: 637.
