При оценки надежности восстанавливаемых ВС большое значение им t восстановления. Надежность таких систем м. оценить рассматривая последовательность отказов-восстановлений. В простейшем случае, когда показатель надежности – параметр потока отказов, временем восстановления пренебрегают. Здесь процесс представляется как последовательность однородных случайных событий отказов – восстановлений.
Им. интерес выявления связей м/ функцией плотности распределения до отказа f(t) и параметром потока отказов w(t).
w(t) выражает среднее количество отказов одного объекта в единицу времени, в условиях восстановления.
f(t) выражает среднее количество отказов в единицу времени в условиях когда восстановление не производится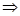 
w(t) м.б. выражена бесконечным рядом:
w(t) = f(t) + f(t)*f1(t) + f(t)*f1(t)*f2(t) + … (1)
* - композиция двух функций плотности, т.е. операцию, заключающуюся в нахождении функции плотности распределения суммы 2-х независимых СВ по заданным функциям плотности распределения последних.
fi(t) – плотность распределения от i-ого восстановления до следующего отказа.
Т.о. I слагаемое – это плотность распределения времени до I отказа. II – до II отказа и т.д.
Операцию * удобно осуществлять в области изображений функций плотностей по Лапласу, т.к. изображение функции плотности суммы СВ = произведению изображений плотностей слагаемых.
Тогда м. переписать формулу:
w*(S) = f*(S) + f*(S )f1*(S) + f*(S)f1*(S)f2*(S) + … (2)
* - изображение соответствующей функции по Лапласу, как функции от оператора S
Полное восстановление означает, что f1(t) = f2(t) = … = f(t).
Аналогичное выражение справедливо и для изображений функции:
w*(S) = f*(S) + f*2(S )f*3(S) + … = f*(S)(1 + f*(S) + f*2(S) + …) (3)
Известно, что |f*(S)|<1. Применив формулу суммы бесконечно убывающей геометрической прогрессии получим:
w*(S) = f*(S)/[1 – f*(S)] (4)
В случае, когда известен w(t) в режиме работы с восстановлением и требуется определить функцию плотности распределения времени до отказа м.б. применена обратная зависимость:
f*(S) = w*(S)/[1 + w*(S)] (5)
Пример: определение параметров потока отказов w(t).
Пусть f(t) = le-lt. Учитывая (4) f*(S) = l/(l + S)
w*(S) = f*(S)/(1 - f*(S)) = l/(l + S)/[1 - l/(l + S)] = l/S
w(t) = l
В случае, когда потери времени восстановления имеют существенное значение для оценки качества эксплуатации аппаратуры, как показатель надежности используется коэффициент готовности.
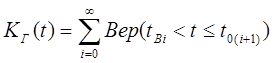
Вер – вероятность выполнения условия в скобках.
Отсюда, при допущении, что восстановление полное, т.е. надежностные свойства объекта после восстановления не меняются, м.б. получено операторное выражение:
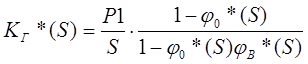(6)
Пример: определение коэффициента готовности. Пусть имеется объект, для которого:
j0(t) = le -lt
jB(t) = me -mt
Тогда: j0*(S) = l/(S + l) jB*(S) = m/(S + m)
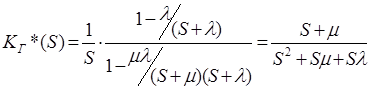
Оригинал
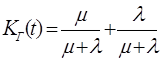.e–(m+l)t (7)
Функция коэффициента готовности:
Если считать, что среднее время восстановления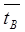 
=1ч, среднее время до отказа 
= 103ч. m>>l
Тогда постоянная времени экспоненты Т = 1/(m+l)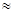 
1/m =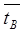 
Переходный процесс для данной задачи = 3-4 часа. Далее можно пользоваться установившемся коэффициентом готовности
КГ УСТ = m/(m+l) (8)
Надежность резервируемых восстанавливаемых ВС
Наиболее подходящими методами для оценки надежности таких систем являются методы, основанные на теории Марковских процессов. Марковские процессы позволяют описывать последовательности отказов-восстановлений в системах, которые описываются при помощи графа состояний (это направленный граф, вершины которого изображают отдельные состояния системы, а дуги – переходы из одного состояния в другое).
В задачах теории надежности каждой комбинации отказовых и работоспособных состояний соответствует 1 состояние системы. Число состояний системы: n = 2k k – количество подсистем.
Чтобы уменьшить число рассматриваемых состояний в случае однородных подсистем, состояния с одинаковым количеством отказавших подсистем объединяются. Тогда общее число состояний системы: n1 = k + 1
определяемое как k отказовых состояний и еще 1 состояние, когда отказов нет.
Наиболее часто для расчета надежности применяется метод Марковских цепей с непрерывным временем, основанный на следующей систему диф. уравнений:
dP/dt = p(t)L (9)
где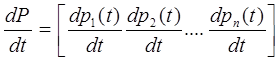 
Матрица интенсивностей переходов:
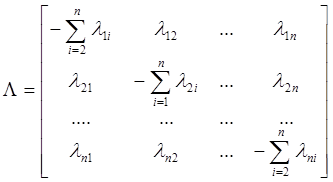(10)
lij – интенсивность перехода системы из i-го состояния в j-ое
рi(t) – вероятность того, что система находится в i-ом состоянии
Часто встречается необходимость оценки надежности достаточно сложных резервных и восстанавливаемых систем, для которых метод Марковских цепей приводит к сложным расчетам из-за большого числа состояний системы.
Дата: 2019-12-10, просмотров: 278.
