Вероятность P_s(t) безотказной работы системы, исходя из независимости отказов, определяется как произведение вероятностей отдельных событий

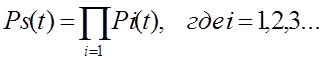               (1)

т.к. то вероятность безотказной работы системы P_s(t) будет .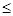

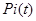Используя формулу связи P_s(t) и ИО P(t)=e^-lt и формулу (1) можно записать, что ИО системы             l_s(t) =                                                     (2)

Принимая во внимание, что среднее время наработки до отказа равно Т= t_B= 1/l, получаем что среднее время до отказа для системы запишется:

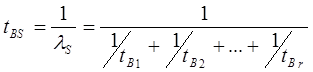                 (3)

оценки, получаемые по (1) (2) (3) являются заниженными. В этих выражениях не учитывается мероприятия, выполняемые для повышенной надежности систем. Например возможный контроль и компенсация погрешностей отдельных компонентов. При расчетах эти факторы м.б. учтены путем введения соответствующих поправочных коэффициентов. Для повышения точности расчетов оценок показателей надежности учитываются известные из опыта эксплуатации временные ресурсы, которые обозначим T_Fi, - работы i-тых отдельных компонентов. Поправочные коэффициенты t_i в этом случае вычисляются по формуле:

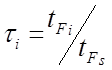                                                         (4)

где 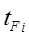 – это среднее время реализации системой функции с участием i-того компонента. Тогда ИО  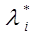   = l_i t_i                                                      (5)

Тогда более точное прогнозируемая оценка ИО системы запишется:

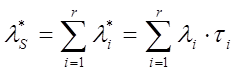                                          (6)

значение l_i представляет собой номинальную оценку ИО i-того компонента. Оценки показателей надежности полученные по (1) (2) (3) можно скорректировать с учетом (5) при использовании (6) предполагая, что если компонент системы не участвует в реализации данной функции, то в заданном интервале времени он не выходит из строя, т.е. ИО в паузе = 0. Такое допущение приемлемо для некоторых типов электромеханических элементов. Для активных полупроводниковых элементов ИО в паузе можно обозначить l_Р и во время функциональной загрузки (реализация задач, функций) l_F примерно равны l_Р 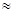 l_F. При их использовании для оценки ИО системы необходимо использовать (2). В реальных условиях эксплуатации электронной аппаратуры, функциональная загрузка отдельных компонентов оказывается различной, поэтому l_F < l_Р. Если при реализации функции (задачи) i-тый компонент характеризуется ИО l_i, то с учетом пауз, в его загрузке эта интенсивность снижается в K_Pi раз.        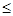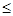l_Pi = K_Pi l_i       причем 0  K_Pi  1.

Реальная продолжительность функционирования i-того элемента определяется выражением (4) с учетом которого можно записать выражение для вычисления более точной оценки ИО отдельного элемента:

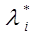= l_i [t_i + K_Pi (1 - t_i)]                                (7а)

ИО для системы из r элементов:

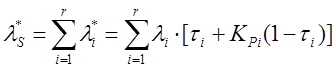             (7б)

Более точные оценки вероятности безотказной работы и среднего времени наработки до отказа можно получить из выражений (1) и (3) с учетом (7).

Поправочные коэффициенты K_Pi определяют опытным путем или по результатам эксплуатации. Они зависят от характера функционирования элементов зависимости ИО компонентов системы, учитывающие влияние перечисленных факторов или функциональную загрузку компонентов.