Общие положения
Важнейшим эксплуатационным показателем качества системы является надежность. Недостаточно высокий уровень, которой приводит к снижению эффективности систем и ошибочным действиям в решении задач. Надежность систем взаимосвязана как с техническими, так и с экономическими требованиями. Надежность характеризует ожидаемое поведение системы в смысле отказа или кратковременная ошибка ее функционирования в заданном интервале времени. Отказ заключается в потере работоспособности, которая м.б. восстановлена только путем внешнего вмешательства.
Случайная ошибка функционирования (сбой) проявляется в кратковременном случайном нарушении выполнения к.л. функции. Если нарушение носит систематический характер, то имеет место устойчивый отказ.
Для количественных оценок надежности используют различные характеристики и параметры, относящиеся к событиям как появление отказа или случайной ошибки функционирования, что позволяет предупредить или устранить их.
Важнейшими из характеристик являются:
- среднее время наработки до отказа;
- готовность аппаратуры;
- вероятность безотказной работы (в течении заданного времени и в заданном режиме);
- частота отказов.
Надежность прибора или системы можно прогнозировать рассчитав ее заранее на этапе проектирования этих систем. Методика расчета основана на знании показателей надежности отдельных компонентов с учетом структуры, принципа и условий эксплуатации системы.
Полученные оценки являются вероятностными, т.е. показатели надежности компонентов оцениваются статистически по результатам их испытаний или эксплуатации.
Законы распределения случайной величины (СВ) и их события.
СВ – величина, которая в результате опыта может принимать то или иное значение, причем заранее не известно какое именно. СВ м.б. дискретной и непрерывной.
Закон распределения СВ – соотношение, устанавливающее связь м/ значениями СВ и их вероятностями. Для характеристики СВ используется вероятность того, что СВ X меньше текущей переменной x.
Функция распределения (ФР) СВ (интегральный закон распределения)
F(x) = p (X < x)
Плотность распределения (ПР) непрерывной СВ (дифференциальный закон распределения) это производная от ФР
f(x) = dF(x) / dx.
Свойства ПР:
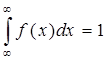
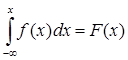
В теории надежности за СВ обычно принимают время работы системы (это время до возникновения отказа). В этом случае ФР:
F(t) = P (t < tзад) = Q(t).
ПР: f(t) = dQ(t) / dt.
Вероятность безотказной работы за время t:
P(t) = 1 – Q(t).
Интенсивность отказа (условная плотность вероятности отказов) – это отношение ПР f(x) к вероятности безотказной работы P(t):
l(t) = f(t) / P(t).
В теории надежности наибольшее распространение получили законы распределения СВ f(t):
Для дискретной СВ – биноминальный, Пуассона.
Для непрерывной СВ – экспоненциальный, нормальный, гамма, Вейбулла, хи квадрат, логарифмический.
Случайное событие это событие, которое в результате опыта может произойти или не произойти. Для нас случайное событие это отказы, восстановления, заявки на обслуживание…образуют случайные потоки и случайные процессы. Поток событий это последовательность событий происходящих одно за другим в какие-то промежутки времени, например отказы восстанавливаемого производства образуют поток отказов. Под их действием, потов отказов и восстановлений, система может находится в различных состояниях: полного отказа, частичного отказа и работоспособном. Переход системы из одного состояния в другое представляет собой случайный процесс.
Описание резервных систем
Резервная система м.б. проста и наглядно представлена в виде связного графа (графа - надежности). Где вершины соответствуют подсистемам, а дуги – соединением между ними. Принимается, что отказ i-ой подсистемы соответствует обрыву i-ого ребра графа. Отказ системы- это потеря связности между двумя выделенными вершинами графа (полюсами).
|
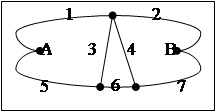
Если считать что дуги 1-7 соответствуют к-л обрабатывающим, запоминающим или коммутирующим устройствам, осуществляющим обработку и передачу информации из А в В, для работы такой системы достаточно наличие одного пути передачи и обработки, то данный граф является графом надежности системы.
Примеры.
Рассмотрим ВС состоящую из устройств памяти y1 и y2, процессоров П7 и П8 и устройств сопряжения С3 – С5. Рисунок в тетради.
Необходимо оценить вероятность безотказной работы системы. Допустим, что условием работоспособности системы является наличие хотя бы одного работающего устройства памяти, хотя бы одного работающего процессора и связи м/ ними через устройство сопряжения. Отказы подсистем являются отказами типа отключения, например отказ y1 не препятствует работе остальной части системы.
Изобразим систему в виде:
графа системы
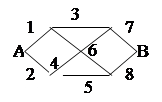
вспомогательного графа:
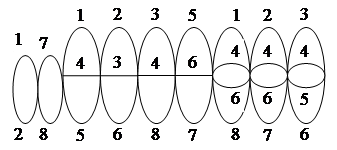
Определим минимальные сечения: 12, 78, 145, 236, 348, 567, 1468, 2467, 3456.
Минимальные пути: 137, 168, 247, 258, 13458, 16547, 24368, 25637,
Пусть вероятность отказа 2-ух устройств в памяти qУ соответственно 4-ех устройств сопряжения qС равны м/ собой, тогда
рН = (1-qУ2). (1-qП2). (1-qС2. qП)2. (1-qС2. qУ)2. (1- qУ. qС2. qП)2. (1-qС4)
обозначим вероятности безотказной работы устройств памяти через рУ = 1-qУ, устройств сопряжения рС = 1-qС, процессоров рП = 1-qП, тогда
рВ = 1 - (1- рУ. рС3. рП)4. (1- рУ. рС. рП)4.
Вспомогательный граф системы для определения рВ.

Мажоритарное резервирование
Простейшая структура устройства преобразования информации с мажоритарным органом:
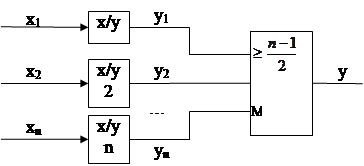
1,2…n – одинаковые устройства преобразования информации, работающие //-о.
Если из-за отказа работы устройств наблюдается расхождение м/ выходами устройств, то мажоритарный орган М выдает тот вариант информации, который наблюдается на большинстве из выхода преобразователей x/y.
Вероятность безотказной работы системы:
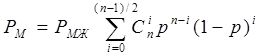
РМЖ, Р - вероятность безотказной работы мажоритарного органа и канала обработки информации. n – д.б. нечетным.
Для троированной системы (n=3) м. записать:
РМ3 = РМЖ(3р2 – 2р2)
n=5: РМ53 = РМЖ(10р3 – 15р4 + 6р5)
Приведенная схема не позволяет достичь вероятность безотказной работы системы >, чем РМЖ. Данный недостаток устранен в мультиплексной схеме:
Здесь мажоритарные органы также резервируются. Первоначальный канал обработки информации разбивается на последовательные участки (слои).
Исправление ошибки, связанной с неисправностью мажоритарного органа происходит через слой резервированных подсистем.
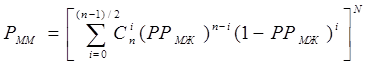
N – число слоев схемы. Р – вероятность безотказной работы схемы в пределах одного слоя.
Встречаются системы с голосованием и реконфигурацией, где после отказа одного устройства из трех, система переходит на работу с одним устройством из оставшихся двух.
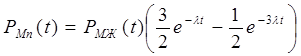
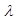 - интенсивность отказа одного канала.
- интенсивность отказа одного канала.
Данная формула справедлива при экспоненциальной модели надежности каналов и при пренебрежении ненадежностью аппаратуры для переключателя.
Контроль в ЭВМ
Контроль в ЭВМ – процессы, обеспечивающие обнаружение ошибок в работе ЭВМ, которые вызваны отказом или сбоем аппаратуры, ошибкой оператора, ошибкой в программе или другими причинами. Контроль необходимо организовывать так, чтобы по возможности контролировались все функции проверяемого объекта. Степень диагностирования определяется полнотой контроля. Количественно полнота контроля оценивается отношением, показывающим относительное число элементов системы, охваченных данным способом контроля. В отдельных случаях целесообразно оценивать полноту контроля как относительное число отказов, которые обнаруживаются данным способом контроля к общему числу отказов.
По признаку применяемых средств контроль в ЭВМ разделяется на:
1) аппаратурный
2) программный
3) смешанный
(1) отличается большим быстродействием, но требует дополнительных аппаратных средств.
(2) Дополнительных аппаратных средств не требует, кроме некоторого дополнительного объема памяти для размещения программного контроля. «-» связан с некоторым расходом дополнительно процессорного времени для выполнения контроля.
Целесообразно сочетать (1) и (2) средства контроля.
По характеру контроля в ЭВМ делят на:
а) оперативный
б) тестовый
(а) осуществляется в ходе решения эксплуатационных задач и позволяет в процессе их решения немедленно обнаруживать ошибку в ходе ее работы. (а) является не полным, т.к.выполняется для случайных неприспособленных для решения контроля задач.
(б) осуществляется в специально отведенные промежутки времени на основе решения спец тестовых задач, он основан на тестах, которые обеспечивают полный контроль всех элементов объекта за минимальное время.
«-»(б): потеря дополнительного процессорного времени
«+»(б): при тестовом контроле упрощается анализ результатов; обеспечивается полнота контроля.
(б) непригоден для обнаружения сбоев аппаратуры в процессе ее эксплуатации.
(б) имеет место тогда, когда результаты тестирования нужны для оценки частоты сбоев в исследуемой аппаратуре.
По способу организации различают контроль:
1) прямой
2) обратный
3) смешанный
При (1) основной вычислительный процесс  , с исходными данными x и результатами y, сопровождается //-ым вычислительным процессом П.
, с исходными данными x и результатами y, сопровождается //-ым вычислительным процессом П.
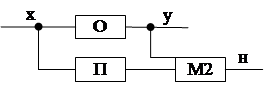
В случае безотказной работы результаты процессов О и П д. совпадать, что определяется устройством сравнения М2. В случае, когда результаты не совпадают М2 выдает сигнал об ошибке н.
Метод позволяет выявлять только сбои и отказы аппаратуры: если процессы О и П осуществляются по одной и той же программе; если они осуществляются по разным, но функционально эквивалентным программам (1) позволяет выявлять ошибки в программах.
«-»(1): - большая трата аппаратных средств; - она м.б. 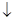 , если О и П выполняются последовательно на одной и той же аппаратуре. Здесь контроль б. выявлять только сбои, а не отказы аппаратуры; -
, если О и П выполняются последовательно на одной и той же аппаратуре. Здесь контроль б. выявлять только сбои, а не отказы аппаратуры; - 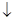 за счет
за счет 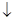 точности.
точности.
Для некоторых задач, которые характеризуются взаимно однозначным соответствием м/ исходными данными и результатом, эффективнее применять (2).
При (2) //-ый процесс П1, с исходными данными y и результатом x, осуществляет обратное преобразование результата контролируемого процесса О.
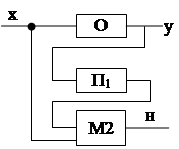
«-»(2): кроме ограниченности класса решаемых задач и в том, что время, затраченное на получение контролируемого решения, даже в случае применения дополнительной аппаратуры будет не ниже суммарного времени выполнения процессов О и П.
В отдельных случаях целесообразно применять смешанный контроль
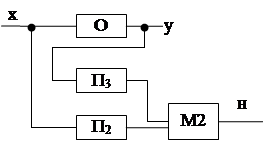
При (3) исходные данные x и результаты y основного вычислительного процесса подвергаются преобразованиям П2 и П3, которые в случае безотказной работы дают сопоставимые результаты.
Все методы контроля имеют свои недостатки, 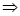 используются комбинации.
используются комбинации.
Модели надежности ПО
Модель Шумана.
Основана на следующих допущениях:
· общее число команд в программе на машинном языке постоянно
· в начале компоновочных испытаний число ошибок = некоторой постоянной величине и по мере не исправления ошибок их становится меньше
· в ходе испытания программы новые ошибки не вносятся
· ошибки изначально различимы. По суммарному числу исправленных ошибок можно судить об оставшихся
· интенсивность отказов программы 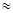 числу оставшихся ошибок
числу оставшихся ошибок
На основе данных допущений получим:
er(x) = e(0) – ec(x) (1)
x – продолжительность отладки программы
e(0) – отношение числа ошибок Е0, имеющихся в программе в момент времени x = 0 к общему числу команд на машинном языке I.
e(0) = Е0/I
ec(x) – число остаточных ошибок в момент времени x, отнесенное к общему числу команд I.
lS(t) = kS.er(x) (2)
t – время работы системы
kS – коэффициент пропорциональности
lS(t) – интенсивность отказов в течении интервала времени t
Определив l программы (частоту появления ошибок) найдем выражение для вероятности безотказной работы
P(t) = exp[–  lS(t)dx] = exp[–
lS(t)dx] = exp[–  kS.er(x)dx] (3)
kS.er(x)dx] (3)
Т.к. в данной модели частота появления ошибок считается независимой от t, она принимается постоянной, 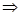 среднее время безотказной работы программы =:
среднее время безотказной работы программы =:
Т0 = 1/lS(t) = 1/(kS.er(x)) (4)
Оценивание параметров модели:
Подставляя (1) в (4) получим следующее выражение для среднего времени безотказной работы:
Т0 = 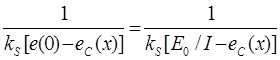 (5)
(5)
(5) содержит 2 неизвестных параметра: kS - коэффициент пропорциональности и Е0, которые можно оценить, используя метод согласования моментов.
Если рассматривать 2 периода отладки программы x1 и x2 такие, что x1 < x2, получаем:
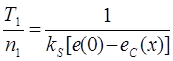 (6)
(6)
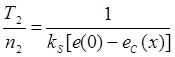 (7)
(7)
Т1, Т2 – продолжительности работы системы, которые соответствуют x1 и x2
n1 и n2 – число ошибок в ПО, обнаруженных в период времени x1 x2
Из (6) и (7) 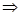
Е0 = 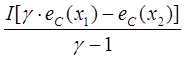 (8)
(8)
где 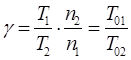
Т0i – среднее время безотказной работы, соответствующее периоду отладки xi
Т0i = Тi/ni
Подставляя (8) в (6), имеем:
КS = 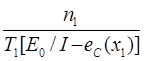 (9)
(9)
Марковская модель.
Основана на допущении: система проходит через последовательность «исправных» (Up) и неисправных (down) состояний. Состояние называется исправным, если после начала компоновки и тестирования программы, ошибка еще не появилась или уже исправлена, а следовательно ошибка еще не появилась.
Диаграмма состояний:
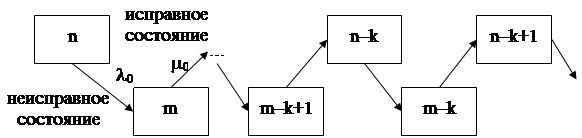
Запишем д.у. состояния для этой системы:
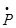 n–k(t) = –lkPn–k(t) + mk–1Nm–k+1(t) (10)
n–k(t) = –lkPn–k(t) + mk–1Nm–k+1(t) (10)
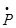 m–k(t) = –mkPm–k(t) + lkPn–k(t) (11)
m–k(t) = –mkPm–k(t) + lkPn–k(t) (11)
Pm–k(0) = 0 k = 1, 2… (12)
Pn(0) = 1 (13)
Решение уравнений (10) и (11) можно получить используя любой из методов численного интегрирования.
После того как будут получены вероятности всех состояний, неготовность системы определится с помощью формулы:
U(t) = 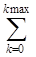 Pm–k(t) (14)
Pm–k(t) (14)
Т.к. вероятности зависят от kMAX, то при больших значениях kMAX можно получить величину U(t) близкую к истинной.
Модель Елинского-Моранды.
данная модуль как и Шумана основана на допущении об экспоненциальном распределении времени безотказной работы ПО. Предполагается, что частота появления ошибок ~ числу остаточных ошибок:
lУМ(xi) = KУМ[E0 – (i – 1)] (15)
KУМ – коэффициент пропорциональности
xi – интервал времени м/ i и u(i-1) ошибкой
С помощью (15) можно найти вероятность безотказной работы:
P(ti) = exp[–KУМ(E0 – i + 1)ti] (16)
Среднее время безотказной работы:
Т0 = 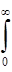 P(ti)dti =
P(ti)dti = 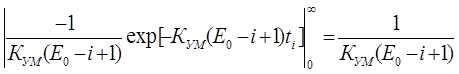 (17)
(17)
Модель Шика-Волвертона.
Основа модели – положение о том, что интенсивность появления ошибок ~ не только количеству оставшихся в программе ошибок, но и времени, потраченному на отладку.
"–" рассмотренных моделей:
- при неточном определении первоначального числа ошибок в программе, интенсивность отказов делается отрицательной;
- здесь предполагается, что после обнаружения ошибка ликвидируется и не вносятся новые ошибки.
В целях преодоления "–" была предложена модель, основанная на допущениях о том, что поток возникновения ситуаций, в которых возможен отказ, является Пуассоновским с параметром l. Однако, по мере обнаружения и исправления ошибок, отказы в этих ситуациях возникают с вероятностью <1. Другими словами, этот поток отказов представляется в виде разреженного потока, с переменным коэффициентом разряжения pi, i – номер отказа.
В простейшем случае:
pi = 1 – (1 – pН)qi–1 (18)
где 0<q<1
pН = p1 – начальный коэффициент разряжения потока.
Данная модель подходит не только для прогнозирования интенсивности следующего отказа, но и для прогнозирования параметра потока отказов.
Из (18) 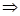 , что изображение параметра потока по Лапласу:
, что изображение параметра потока по Лапласу:
w*(S) = 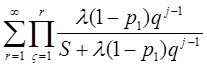 (19)
(19)
Приближенное значение оригинала:
w(t) = (1–p1)l – ((1–p1)l)2(1–q)t + ((1–p1)l)3(1–q)(1–q2)t2/2!–...–(–1)n.((1–p1)l)n+1(1–q) ––…(1–qn)tn/n!
с погрешностью не более:
Dw(t) = (–1)n+1((1–p)l)n+2(1–q)…(1–qn+1En+1)/(n+1)! (20)
Приведенные модели представляют интерес прежде всего для прогнозирования отказов в процессе эксплуатации и отладки. Здесь значение параметров определяется в рабочем режиме.
Метод контрольных функций
Наряду с вычислительной функцией по иной программе определяется некоторая функция, которая находится с основной, в некоторых соотношениях, которые называются контрольными соотношениями.
Простейшим примером применения контрольных соотношений является вычисление функций sinx и cosx по отдельным соотношениям.
Общие положения
Важнейшим эксплуатационным показателем качества системы является надежность. Недостаточно высокий уровень, которой приводит к снижению эффективности систем и ошибочным действиям в решении задач. Надежность систем взаимосвязана как с техническими, так и с экономическими требованиями. Надежность характеризует ожидаемое поведение системы в смысле отказа или кратковременная ошибка ее функционирования в заданном интервале времени. Отказ заключается в потере работоспособности, которая м.б. восстановлена только путем внешнего вмешательства.
Случайная ошибка функционирования (сбой) проявляется в кратковременном случайном нарушении выполнения к.л. функции. Если нарушение носит систематический характер, то имеет место устойчивый отказ.
Для количественных оценок надежности используют различные характеристики и параметры, относящиеся к событиям как появление отказа или случайной ошибки функционирования, что позволяет предупредить или устранить их.
Важнейшими из характеристик являются:
- среднее время наработки до отказа;
- готовность аппаратуры;
- вероятность безотказной работы (в течении заданного времени и в заданном режиме);
- частота отказов.
Надежность прибора или системы можно прогнозировать рассчитав ее заранее на этапе проектирования этих систем. Методика расчета основана на знании показателей надежности отдельных компонентов с учетом структуры, принципа и условий эксплуатации системы.
Полученные оценки являются вероятностными, т.е. показатели надежности компонентов оцениваются статистически по результатам их испытаний или эксплуатации.
Законы распределения случайной величины (СВ) и их события.
СВ – величина, которая в результате опыта может принимать то или иное значение, причем заранее не известно какое именно. СВ м.б. дискретной и непрерывной.
Закон распределения СВ – соотношение, устанавливающее связь м/ значениями СВ и их вероятностями. Для характеристики СВ используется вероятность того, что СВ X меньше текущей переменной x.
Функция распределения (ФР) СВ (интегральный закон распределения)
F(x) = p (X < x)
Плотность распределения (ПР) непрерывной СВ (дифференциальный закон распределения) это производная от ФР
f(x) = dF(x) / dx.
Свойства ПР:
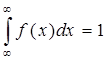
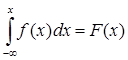
В теории надежности за СВ обычно принимают время работы системы (это время до возникновения отказа). В этом случае ФР:
F(t) = P (t < tзад) = Q(t).
ПР: f(t) = dQ(t) / dt.
Вероятность безотказной работы за время t:
P(t) = 1 – Q(t).
Интенсивность отказа (условная плотность вероятности отказов) – это отношение ПР f(x) к вероятности безотказной работы P(t):
l(t) = f(t) / P(t).
В теории надежности наибольшее распространение получили законы распределения СВ f(t):
Для дискретной СВ – биноминальный, Пуассона.
Для непрерывной СВ – экспоненциальный, нормальный, гамма, Вейбулла, хи квадрат, логарифмический.
Случайное событие это событие, которое в результате опыта может произойти или не произойти. Для нас случайное событие это отказы, восстановления, заявки на обслуживание…образуют случайные потоки и случайные процессы. Поток событий это последовательность событий происходящих одно за другим в какие-то промежутки времени, например отказы восстанавливаемого производства образуют поток отказов. Под их действием, потов отказов и восстановлений, система может находится в различных состояниях: полного отказа, частичного отказа и работоспособном. Переход системы из одного состояния в другое представляет собой случайный процесс.
Законы распределения, используемые в теории надежности.
Биноминальный закон распределения числа n – появления события А в m – независимых опытах (испытаниях). Если вероятность появления события А в одном испытании есть р, тогда вероятность не появления события q = 1 – p.
Если независимое число испытаний = m, тогда вероятность появления n событий будет равна: 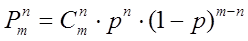 - уравнение Бернулли.
- уравнение Бернулли.
 - число сочетаний из m по n.
- число сочетаний из m по n. 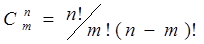 .
.
Свойства:
1) число событий n это целое положительное число;
2) математическое ожидание (МО) числа событий М = m*p;
3) среднеквадратическое отклонение 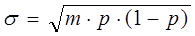
При увеличении числа испытаний биноминальное распределение приближается к нормальному со средним значением n/m и дисперсией p(1-p)/m.
Закон Пуассона.

вероятность возникновения случайного события n раз за время t. l - интенсивность случайного события.
Свойства:
1) МО числа событий за время t: М = l*t.
2) среднеквадратическое отклонение числа событий  , для данного распределения М = D.
, для данного распределения М = D.
Распределение Пуассона получается из биноминального, если число испытаний m неограниченно возрастает, а МО числа событий остается постоянным.
Закон Пуассона используется в том случае когда необходимо определить вероятность того что за данное время произойдет 1,2,3…отказов.
Экспоненциальный закон.
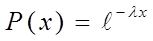
где P(x) это вероятность того что СВ X имеет значение большее x.
В частном случае, когда за СВ принимается время работы системы t вероятность т ого что система на протяжении времени t будет находится в работоспособном состоянии будем равно: 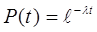 .
.
где l - интенсивность отказов системы. l – const.
Это выражение можно получить из закона Пуассона, если число отказов n = 0.
Вероятность отказа за время t м.б. записана
Q(t) = 1 – P(t) = 1 - 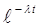
Плотность вероятности отказов
F(t) = dQ / dt = l 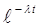
Среднее время работы до возникновения отказа
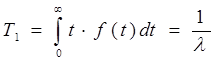
Дисперсия – это время работы до возникновения отказа
D(t) = 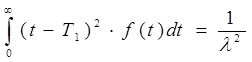
Среднеквадратичное отклонение
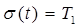
Равенство 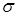 и Т1 является характерным признаком экспоненциального распределения.
и Т1 является характерным признаком экспоненциального распределения.
g распределение.
Если отказ устройства возникает тогда когда произойдет не менее k отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметром l0. Плотность вероятности отказа устройства: 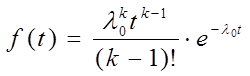
где l0 исходная интенсивность отказов (ИО) элементов устройства, отказ которого вызывается отказом его элементов. Этому распределению подчиняется время работы резервных устройств и систем.
Вероятность k и более отказов, т.е. вероятность отказа устройства:
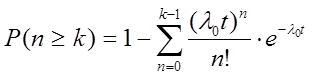
Плотность вероятности отказа системы за время t:
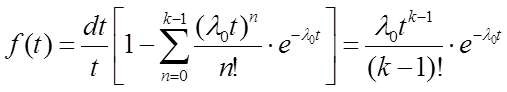
Среднее время работы системы до отказа: 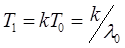
ИО устройства:

Вероятность безотказного состояния системы:
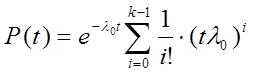
При k = 1 g распределение совпадает с экспоненциальным.
Распределение Вейбула.
Плотность вероятности: 
Вероятность отсутствия отказа за время t: 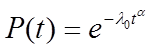
ИО: 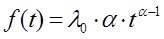
a и l0 - параметры распределения, при a = 1 функция Вейбула совпадает c экспоненциальным распределением. При a < 1 ИО будет монотонно убывающей функцией, если a > 1 – монотонно возрастающей.
Распределение Вейбула применяется для отказов устройства состоящего из последовательно соединенных дублированных элементов.
Нормальное распределение (НР).
СВ X возникает тогда когда x зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из факторов по сравнению с влиянием совокупности остальных незначительно.
Плотность вероятности отказа НР:

Вероятность отказа за время t:
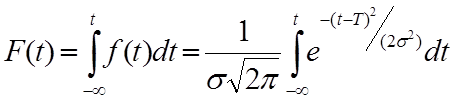
Для удобства определения F(t) составлены таблицы. Значение функции распределения определяется формулой: F(t) = 0.5 + Ф(u) = Q(t)
U = (t – T)/ 
Вероятность отсутствия отказа за время t:
P(t) = 1 – Q(t) = 1 – (0.5 + Ф(u)) = 0.5 - Ф(u)
ИО монотонно возрастает и постепенно начинает приближаться к асимптоте:
y = (t – T)/ 
c2 – распределение.
Если CB t распределена по НЗ с Т = 0 и  = 1, то параметр X =
= 1, то параметр X = 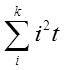 будет являться СВ с плотностью распределения:
будет являться СВ с плотностью распределения:
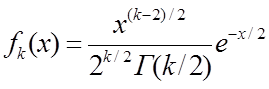
где k- число степеней свободы; Г(k/2) – это g функция.
С увеличением k c2 распределение приближается в НР.
g функция от k/2 это 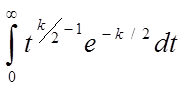
НР находит широкое применение в теории надежности. Например установлено, что описание удвоенного значения наработки изделия, отнесенное к среднему времени безотказной работы имеет c2 распределение, если время до отказа - СВ с экспоненциальным распределением.
Дата: 2019-12-10, просмотров: 428.