Определение 2.1.11. Формула F(x1,…,xn) называется тождественно истинной или общезначимой, если для любой интерпретации φ при любых значениях свободных переменных x1=a1,…,xn=an выполняется F(a1,…,an)=1.
Формула F(x1,…,xn) называется выполнимой, если существует интерпретация φ и значения свободных переменных x1=a1,…,xn=an такие, что F(a1,…,an)=1.
Формула F(x1,…,xn) называется невыполнимой или противоречивой, если для любой интерпретации φ при любых значениях свободных переменных x1=a1,…,xn=an выполняется F(a1,…,an)=0.
Упражнение2.1.6
Доказать, что формулы F(x1,…,xn) и G(x1,…,xn) равносильны тогда и только тогда, когда формула F(x1,…,xn) ~G(x1,…,xn) тождественно истинна.
2.1.8. Рассуждения в логике высказываний (предикатов)
Одна из основных целей изучения логики состоит в получении возможности построения базы знаний, позволяющей накапливать знания в виде формул и выводить возможные следствия из этих знаний.
Определение 2.1.12. Рассуждением называется конструкция вида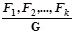 
,гдеF1,F2,…,Fk,-называются посылками, а G-следствием, F1,F2,…,Fk, G – формулы логики высказываний (предикатов)..
Пример 2.1.9
, 
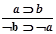-известно, что эти рассуждения – верные.
-, 
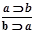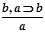- -неверные рассуждения.
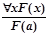--верное рассуждение.
-- неверное рассуждение.
Определение 2.1.13. Рассуждение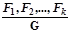 
называется верным (формула G в этом случае называется логическим следствием формул F1,F2,…,Fk,), если для любой интерпретации φ (в логике предикатов, дополнительно, - для любых значений свободных переменных), для которой выполняются условия φ(F1)=φ(F2)=…=φ(Fk)=1, выполняется также φ(G)=1.
Упражнение 2.1.7
Доказать, что рассуждение 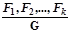верно тогда и только тогда, когда формула F1&F2&…&Fk,ÉG является тождественно истинной (общезначимой).
Упражнение 2.1.8
Доказать, что рассуждение 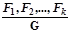верно тогда и только тогда, когда формула F1&F2&…&Fk, &ØG является невыполнимой (противоречивой).
2.2. Метод резолюций
Назначение метода резолюций - доказательство того, что формула G является логическим следствием формул F1,F2,...,Fk. В основе метода лежит доказательство невыполнимости формулы F1&F2&…&Fk&ØG. Рассматриваемая формула приводится к кнф и кнф рассматривается как множество дизъюнктов. Дизъюнкт же может представляться, как множество литер.
Метод резолюций в логике высказываний
Определение 2.2.1. Литеры L и L называются противоположными или контрарными.
Метод резолюций предполагает процедуру порождения новых дизъюнктов из заданного множества. В логике высказываний она основана на правиле резолюций.
Определение 2.2.2. Правилом резолюций в логике высказываний называется следующее правило:
из дизъюнктов ХvF и XvG выводим дизъюнкт FvG.
Упражнение 2.2.1
Доказать правильность рассуждения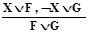 
.
Пример 2.2.1
Исходные дизъюнкты: XvYvZ, XvY. По правилу резолюций выводим дизъюнкты:
YvZvY (контрарные литеры X и X)
XvZvX (контрарные литеры Y и Y).
Если исходные дизъюнкты X и X, из этой пары выводим дизъюнкт, не содержащий ни одной литеры. Будем называть его пустым и обозначать знаком «□». Пустой дизъюнкт равносилен значению 0. Значит F&□º□ и Fv□ ºF.
Определение 2.2.3. Пусть S – множество дизъюнктов. Выводом из S называется последовательность дизъюнктов
D,D2,...,Dn
такая, что каждый дизъюнкт этой последовательности принадлежит S или следует из предыдущих по правилу резолюций. Дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.
Пример 2.2.2
Исходное множество дизъюнктов: S={XvYvZ, YvU, X}. Рассмотрим последовательность:
D1=XvYvZ, D1ÎS.
D2=YvU, D2ÎS.
D3=XvZvU, следует из D1, D2 по правилу резолюций.
D4=X, D4ÎS.
D5=ZvU, следует из D3, D4 по правилу резолюций.
Рассматриваемая последовательность является выводом из S и дизъюнкт ZvU выводим из S.
Применение метода резолюций основано на следующей теореме.
Теорема 3. Множество дизъюнктов логики высказываний S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.
Пример 2.2.3
Докажем, что формула G=Z является логическим следствием формул F1=XvYÉX&Z, F2=YÉZ. Для этого нужно доказать невыполнимость формулы F1&F2&Gº (XvYÉX&Z)&(YÉZ)&Z. Приведем ее к кнф.
(XvYÉX&Z)&(YÉZ)&Zº((XvY)v(X&Z))&(YvZ)&Zº((X&Y)v(X&Z))&(YvZ)&Zº(X&(YvZ))&(YvZ)&ZºX&(YvZ)&(YvZ)&Z
Тогда исходное множество дизъюнктов S={X, YvZ, YvZ, Z}. Вывод пустого дизъюнкта:
D1=YvZ, D1ÎS.
D2=Z, D2ÎS.
D3=Y, следует из D1, D2 по правилу резолюций.
D4=YvZ, D4ÎS.
D5=У, следует из D2, D4 по правилу резолюций.
D6=□.
Пустой дизъюнкт выводим из S, следовательно, формула G является логическим следствием формул F1, и F2, ч. т. д.
2.2.2. Подстановка и унификация
Формулы логики предикатов содержат переменны, поэтому для сопоставления литер необходимо осуществлять подстановки вместо переменных их значений.
Определение 2.2.4. Подстановкой называется множество подстановочных компонент вида
s={x1=t1, x2=t2,…, xn=tn},
где x1,x2,…,xn – различные переменные, t1,t2,…,tn – термы, причем терм ti не содержит переменной xi (1≤ i ≤ n).
Если σ = (x1=t1,...,xn=tn) – подстановка, а F – некоторый объект логики предикатов (терм, дизъюнкт, формула, множество объектов и т. д.), то через σ(F) будем обозначать дизъюнкт, полученный из F одновременной заменой всех xi на ti,.
Пример 2.2.4.
если σ={x=f(y), y=c, z=g(u)), F=R(x, y, z)vP(f(y)), то σ(F)=R(f(y), c, g(u))vP(f(c).
Определение 2.2.5. Пусть {E1,…,Ek} – множество объектов логики предикатов. Подстановка σ называется унификатором этого множества, если σ(E1)=σ(E2)=…=σ(Ek). Множество унифицируемо, если существует унификатор этого множества.
Пример 2.2.5.
Множество атомарных формул {Q(a,x,f(x)), Q(u,у,z)} унифицируемо подстановкой {u=a, x=у, z=f(у)},
а множество {R(x,f(x)), R(u,u)} неунифицируемо.
Если множество унифицируемо, то существует, как правило, не один унификатор этого множества, а несколько. Среди всех унификаторов данного множества выделяют так называемый наиболее общий унификатор.
Определение 2.2.6. Пусть ξ и η – две подстановки. Тогда произведением (композицией) подстановок ξ и η (η◦ξ) называется подстановка z такая, что для любого объекта E выполняется равенство z(E)=η(ξ(E)).
Будем конструировать подстановку z следующим образом:
Алгоритм 1. Конструирование композиции подстановок.
Вход: подстановки ξ={x1=t1, x2=t2,…, xk=tk} и η={y1=s1, y2=s2,…, yl=sl}
1) получим из подстановок η и ξ множество подстановочных компонент {x1=η(t1), x2=η(t2),…,xk=η(tk), y1=s1, y2=s2,…, yl=sl},
2) удалим из него компоненты вида xi=xi для, если таковые найдутся для 1≤ i≤ k,
3) удалим компоненты вида yj=sj, если yj Î{x1,…, xk}, для 1≤j≤l, получим подстановку z=η◦ξ.
Пример 2.2.6
Рассмотрим пример. Пусть ξ = {x=f(y), z=y, u=g(d)}, η = {x=c, y=z}.
1) {x=f(y), z=z, u=g(d), x=c, y=z}.
2) {x=f(y), u=g(d), x=c, y=z}.
3) η◦ξ = {x=f(y), u=g(d), y=z}.
Упражнение 2.2.2.
Доказать, что результатом алгоритма 1 является композиция подстановок, удовлетворяющая определению 2.2.6.
Упражнение 2.2.3.
Доказать, что композиция подстановок ассоциативно, т.е. для любых подстановок ξ, η, ζ выполняется равенство ξ◦(η◦ζ)=(ξ◦η)◦ζ.
Введем пустую подстановку – подстановку, не содержащую подстановочных компонент. Будем обозначать ее через ε.
Упражнение 2.2.4.
Доказать, что пустая подстановка является единицей относительно умножения, т.е. для любой подстановки σ выполняются равенства σ◦ε=ε◦σ=σ.
Определение 2.2.7. Унификатор σ называется наиболее общим унификатором (НОУ), если для любого унификатора τ того же множества существует подстановка ξ такая, что τ=ξ○σ.
Пример 2.2.7
Для множества {P(x,f(а), g(z)), P(f(b),y,v)} наиболее общим унификатором является подстановка σ={x=f(b), y=f(a), v=g(z)}. Подстановка τ={x=f(b), y=f(a), z=c, v=g(c)}, то ξ={z=c} также является его унификатором. Однако τ=ξ○σ где ξ={z=c}.
Для изложения алгоритма нахождения наиболее общего унификатора потребуется понятие множества рассогласований в множестве объектов. Множество рассогласований строится следующим образом.
Алгоритм 2. Построение множества рассогласований.
Вход: множество объектов логики предикатов М, каждый объект представляет собой последовательность символов.
1) выделим первую слева позицию (позицию рассогласований), в которой не для всех объектов стоят одинаковые символы.
2) в каждом объекте выпишем подобъект, которое начинается с данной позиции (этими подобъектами могут быть литера, атомарная формула, терм).
3) множество полученных подобъектов называется множеством рассогласований в М.
Пример 2.2.8.
M={P(x, f(y), a), P(x,u, g(y)), P(x, c, v)}, позиция рассогласований – пятая, множество рассогласований - {f(y), u, c}.
M={P(x, y), P(a, g(z))}, позиция рассогласований – первая, множество рассогласований - {P(x, y), P(a, g(z))}.
M={P(x, y),Q(a, v)}, позиция рассогласований – вторая, множество рассогласований - {P(x, y), Q(a, v)}.
Алгоритм 3. Алгоритм унификации.
Вход: множество литер М, каждая литера представляет собой последовательность символов.
1) Положить k=0, Mk=M, σk=ε.
2) Если множество Мk состоит из одной литеры, то выдать σk в качестве НОУ, завершить работу иначе найти множество Nk рассогласований в Mk.
3) Если в множестве Nk существует переменная vk и терм tk, не содержащий vk, то перейти к шагу 4, иначе множество М неунифицируемо, завершить работу.
4) Положить σk+1={vk,=tk}○σk,. К множеству Mk применить подстановку vk=tk, полученное множество литер взять в качестве Mk+1.
5) Положить k=k+1 и перейти к шагу 2.
Пример 2.2.9.Проиллюстрируем работу алгоритма унификации на множестве М.
М={P(x,f(y)), P(a,u)}.
· 1). k=0, σ0=ε, M0=M,
· 2). N0={x,a},
· 3)-4). σ1={x=a}, M1={P(a,f(y)),P(a,u)},
· 5). k=1,
· 2). N1={f(y), u},
· 3)-4). σ2={x=a, u=f(y)}, M2={P(a,f(u))},
· 5). k=2,
· 2). НОУ={x=a, u=f(y)}. Конец работы.
M={P(x,f(y)), P(a,b)}.
· 1). k=0, σ0=ε, M0=M,
· 2). N0={x,a},
· 3)-4). σ1={x=a}, M1={P(a,f(y)), P(a,b)},
· 5). k=1,
· 2). N1={f(y), b},
· 3) М неунифицируемо. Конец работы.
Упражнение 2.2.5.
Доказать, что алгоритм 3 правильно (в соответствии с определениями) оценивает унифицируемость множества литер и находит НОУ.
Дата: 2016-10-02, просмотров: 229.
