МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра «Математическое обеспечение
Автоматизированных систем управления»
С.А.Cавушкин
РЕКУРСИВНО-ЛОГИЧЕСКОЕ
ПРОГРАММИРОВАНИЕ
Учебное пособие для студентов специальностей
«Программное обеспечение вычислительной техники и
Автоматизированных систем» и «Математическое
Обеспечение и администрирование автоматизированных
Систем»
Москва – 2009
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра «Математическое обеспечение
Автоматизированных систем управления»
С.А.Cавушкин
РЕКУРСИВНО-ЛОГИЧЕСКОЕ
ПРОГРАММИРОВАНИЕ. ТЕОРИЯ И ПРАКТИКА.
Рекомендовано редакционно-издательским советом
университета в качестве учебного пособия для
студентов специальностей «Программное обеспечение
Вычислительной техники и автоматизированных
Систем» и «Математическое обеспечение и
Администрирование автоматизированных систем»
Москва – 2009
УДК 519.6, 519.852
Cавушкин С.А. Рекурсивно-логическое программирование. Теория и практика. Учебное пособие для студентов специальностей “Программное обеспечение вычислительной техники и автоматизированных систем” и “Математическое обеспечение и администрирование автоматизированных систем”. - М.: МИИТ, 2009 - 88 с.
В учебном пособии излагаются сведения по математической логике, которые лежат в основе языка ПРОЛОГ и логического программирования. Описаны синтаксис и семантика языка ПРОЛОГ. Семантика языка тесно увязана с методом резолюций для логики предикатов. Сформулированы варианты заданий и методические указания для выполнения лабораторных работ.
Рецензенты: зав. кафедрой ВСС МИИТа кандидат техн. наук, доцент В. Н. Нагинаев
© Московский государственный
университет путей сообщения
(МИИТ), 2009

Подписано к печати – Изд №??-09 Формат – 60х84/16
Усл.-п. л. – 5,5 Заказ № Тираж – ??? экз

127994, Москва, ул. Образцова, 15
Типография МИИТа
СОДЕРЖАНИЕ
1. Парадигмы программирования. 5
2. Теоретические основы логическоого программирования. 7
2.1. Логика высказываний и логика предикатов. 7
2.1.1. Формулы. Синтаксис и семантика формул. 7
2.1.2. Интерпретация формул в логике высказываний. 11
2.1.3. Интерпретация в логике предикатов первого порядка. 12
2.1.4. Равносильность формул логики высказываний. 16
2.1.5. Тождественная истинность формул логики высказываний. 18
2.1.6. Равносильность формул логики первого порядка. 19
2.1.7. Тождественная истинность, общезначимость, выполнимость, противоречивость формул логики предикатов 21
2.1.8. Рассуждения в логике высказываний (предикатов) 21
2.2. Метод резолюций 23
2.2.1. Метод резолюций в логике высказываний. 23
2.2.2. Подстановка и унификация. 25
2.2.3. Метод резолюций для логики первого порядка. 29
2.2.4. Стратегии метода резолюций. 34
2.3. Отношения и предикаты. 39
3. ПРОЛОГ- ЯЗЫК РекуРсивно-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ. 40
3.1. ПРОЛОГ-история возникновения 40
3.2. Синтаксис языка ПРОЛОГ. 40
3.3. Семантика языка ПРОЛОГ. 42
3.4. Язык ПРОЛОГ и метод резолюций. Логическая интерпретация языка Пролог. 48
3.5. Работа в пролог-системе 49
3.6. Описание инфиксных операций 50
3.7. Списки в языке ПРОЛОГ. 51
3.8. Арифметика в языке ПРОЛОГ. 57
3.9. Отсечение и отрицание в языке ПРОЛОГ. 59
3.10. Встроенные предикаты языка ПРОЛОГ. 61
3.11. Работа с базой данных в языке ПРОЛОГ. 64
3.12. Предикаты поиска 68
3.13. Решение головоломки на языке ПРОЛОГ(задача Эйнштейна) 69
4. ЛАБОРАТОРНЫЕ РАБОТЫ ПО РекуРсивно-ЛОГИЧЕСКОМУ ПРОГРАММИРОВАНИЮ 75
4.1. ЗАДАНИЕ N1 Отношения между объектами. (на Прологе и Паскале) 75
4.1.1. Методические указания. 75
4.1.2. Варианты. 76
4.2. ЗАДАНИЕ N2. Работа со списками 80
4.2.1. Методические указания. 80
4.2.2. Варианты. 81
4.3. ЗАДАНИЕ N3. Разные задачи 84
4.3.1. Методические указания. 84
4.3.2. Варианты. 85
4.4. Содержание отчета 88
ЛИТЕРАТУРА. 90
Парадигмы программирования
Парадигма (от греч. παράδειγμα, «пример, модель, образец») — осмысление мира на основе идей, взглядов и понятий. Современное значение этого термина в философии науки используется для обозначения исходной концептуальной схемы, модели постановки проблем и их решения, методов исследования.
Под парадигмой программирования будем понимать систему взгляд, подходов, позиций, определяющую стиль программирования на концептуальном уровне. Парадигма программирования представляет (и определяет) то, как программист видит процесс выполнения программы и, в конечном счете, саму программу.
В литературе формулируется большое число парадигм программирования. Мы выделим следующие:
Императивное программирование — процесс вычисления описывается в виде последовательности команд, изменяющих состояние вычислительной среды. Этот стиль программирования является традиционным и связывается с именем фон Неймана, который разработал основные архитектурно-функциональные принципы построения вычислительных машин (программного управления выполнением программы, хранимой в памяти программы, счетчик команд), которые легли в основу понятия фон-Неймановской архитектуры вычислительных устройств и фон-Неймановского стиля программирования.
Процедурное программирование — часто используется как синоним императивного программирования. При этом команды реализуются вызовами процедур.
Объектно-ориентированное программирование — программа – это набор взаимодействующих объектов. Каждый объект обладает набором свойств, а также набором методов - программ, которые связывают значения свойств объекта и различных объектов друг с другом.
Функциональное программирование — программа представляется в виде композиции и суперпозиции функций. Программы не представляют собой последовательности инструкций и не имеют глобального состояния.
Логическое программирование — программа обычно определяет, что надо вычислить, а не то, как это надо делать. Выполнение программы основано на выводе новых утверждений из набора исходных утверждений, согласно заданным логическим правилам вывода.
Структурное программирование — в настоящее время общепринятая методология, в основе которой лежит представление программы в виде иерархии структур управления (последовательное исполнение операций, ветвление в зависимости от выполнения некоторого заданного условия, цикл, вызов подпрограмм). Разработка программы ведётся пошагово, методом «сверху вниз». Исторически возникло из традиционного императивного программирования путем ограничения применения «неструктурных» операторов, таких как оператор GOTO (безусловного перехода). Использование произвольных переходов в тексте программы приводило к получению запутанных, программ, по тексту которых практически невозможно понять порядок исполнения и взаимозависимость фрагментов.
Программа, управляемая данными — программа представляется в виде графа с вершинами двух видов – процедуры и данные. Данные могут быть входами и выходами процедур. Программа запускается посредством запроса вида «ДАНО-НАЙТИ».
Из выбранных парадигм нас интересуют императивное программирование и его разновидности, как представляющие традиционный стиль программирования, а также логическое программирование, которое является темой данного пособия. Остальные парадигмы приведены в качестве примеров.
Пример 2.1.1
(X&Y)É(XvZ), ((X&Y)ÉZ) –формулы,
X&YvZ, X~YÉZ – не формулы
Соглашение о скобках.
Для уменьшения количества скобок
q во-первых, самые внешние скобки в формуле можно опускать,
q во вторых, вводится приоритет связок.
o имеет наивысший приоритет,
o & и v имеют более низкий одинаковый приоритет,
o É и ~ имеют также одинаковый еще более низкий приоритет.
Таким образом, формулу ((X&Y) ÉZ) можно записать так: X&YÉZ.
Определение 2.1.3. Подформулой атомарной формулы является она сама. Подформулами формулы F являются она сама и все подформулы формулы F. Подформулами формул F&G, FvG, FÉG, F~G являются они сами и все подформулы формул F и G/
Пример 2.1.2
Формула F=X&YÉXvZ имеет шесть подформул: X, Y, Z, X&Y, XvZ, X&YÉXvZ.
Семантика.
Неформально семантика формул логики высказываний определяется следующим образом:
· буквами обозначаются высказывательные переменные;
· (F&G) - называется конъюнкцией высказываний F и G; соответствует высказыванию «F и G»;
· (FÚG) - называется дизъюнкцией высказываний F и G; соответствует высказыванию «F или G»;
· F - называется отрицанием высказывания F; соответствует высказыванию «не F»;
· (FÉG) - называется импликацией высказываний F и G; соответствует высказыванию «если F то G»;
· (F~G) - называется эквиваленцией высказываний F и G. соответствует высказыванию «F тогда и только тогда, когда G».
Формально семантика формул логики высказываний определяется с использованием понятия «интерпретация» (см. далее).
Перейдем теперь к изложению теории, которая является расширением логики высказываний и называется логикой предикатов первого порядка. Для краткости ее называют просто логикой предикатов или просто логикой первого порядка. Отличие и преимущество логики предикатов в том, что простые высказывания в ней не являются неделимыми, как в логике высказываний, а выражаются в виде отношений между предметными переменными и константами. Например, следующие высказывания «Всякое целое число является рациональным», «Число 2 – целое», «2 – рациональное число» с точки зрения логики высказываний являются различными, не связанными друг с другом. С точки зрения логики предикатов высказывания «Всякое целое число» и «Число 2 – целое» связаны с общим отношением «Быть целым числом». Также связаны высказывания «Число является рациональным» и «2 – рациональное число».
Прежде всего, поясним понятие предиката. Предикат – это выражение, очень похожее на высказывание, но в отличие от него, содержащее переменные. Можно сказать, что предикат обращается в высказывание при замене этих переменных конкретными значениями.
Определения в логике предикатов построены аналогично соответствующим определениям в логике высказываний.
При определении используется алфавит, состоящий из символов:
1) предметные переменные, обозначаются буквами x, y, z и др. и предметные константы;
2) функциональные символы, обозначаются буквами f, g, h и др.;
3) предикатные символы, обозначаются буквами P, Q, R и др.;
4) символы истины и лжи;
5) логические связки: &, v, , É, ~;
6) скобки: (, );
7) кванторы 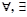
Определение 2.1.4. Термом называется
1) предметная переменная или константа;
2) выражение вида f(t1,…,tn), где t1,…,tn – термы, а f – n-местный функциональный символ.
Определение 2.1.5. Атомарной формулой называется выражение вида P(t1,…,tn), где t1,…,tn – термы, P – символ n-местного предиката.
Определение 2.1.6. Формулой логики первого порядка называется
1) атомарная формула,
2) выражения вида (F)&(G), (F1)v(G), (F), (F)É(G),(F) ~ (G), 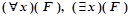 , где F и G – формулы логики предикатов, x – переменная.
, где F и G – формулы логики предикатов, x – переменная.
Формула F в двух последних выражениях называется областью действия квантора по переменной x.
Примем соглашение о приоритете операций, в котором к принятому в логике высказываний (см. выше «Соглашение о скобках»), добавим следующее:
o кванторы имеют одинаковый приоритет, который выше приоритета всех связок.
Пример 2.1.3
P(f(x,y),g(x))&Q(x,y), 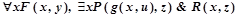 , ((P(f(x,y),g(x))&Q(x,y))ÉR(g(x))) –формулы,
, ((P(f(x,y),g(x))&Q(x,y))ÉR(g(x))) –формулы,
Q(x,y)& Q(x,y)v Q(x,y), Q(x,y)~ Q(x,y)É Q(x,y) – не формулы
Определение 2.1.7. Вхождение переменной в формулу называется связанным, если переменная входит в область действия квантора по этой переменной. В противном случае вхождение называется свободным.
Пример 2.1.4
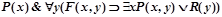 ,
,
Первое и второе вхождение переменной x свободны, третье связано. Все вхождения переменной y связаны.
Определение 2.1.8. Переменная называется свободной в формуле, если существует хотя бы одно свободное вхождение переменной в формулу.
Если x1,…,xn – свободные переменные формулы F, то эту формулу будем обозначать через F(x1,…,xn).
Для неформального представления о семантике формул логики предикатов к соответствующему описанию для логики высказываний (см. выше «Семантика») добавим следующее:
· предметные переменные и константы обозначают некоторые объекты рассматриваемой предметной области, например, числа, люди, автомобили и т. д., в зависимости от того, какая задача решается;
· функциональные символы обозначают функциональные связи между объектами, например, арифметические функции, функции, выдающие сведения о людях или автомобилях, в соответствующих задачах;
· предикатные символы обозначают отношения между объектами, например, отношения сравнения чисел (<, >, и т. д.), отношения между людьми (родственные, дружеские, производственные и т. д.), отношения между людьми и автомобилями (автомобиль принадлежит человеку и т. д.);
· 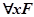 соответствует высказыванию «Для каждого x выполняется F», квантор
соответствует высказыванию «Для каждого x выполняется F», квантор 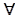 называется квантором всеобщности;
называется квантором всеобщности;
· 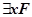 соответствует высказыванию «Существует x, для которого выполняется F», квантор
соответствует высказыванию «Существует x, для которого выполняется F», квантор 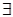 называется квантором существования.
называется квантором существования.
Формально семантика формул логики предикатов определяется с использованием понятия «интерпретация».
Пример 2.1.3
Пусть φ(X)=1, φ(Y)=0, φ(Z)=1, F=XvYÉZ, G=X&Y~Y&Z.
Тогда φ(F)=1, φ(G)=0.
При указании истинностных значений формул будем опускать символ интерпретации, т. е. вместо φ(F)=1, φ(G)=0 будем писать просто F=1, G=0, если это не приводит к неоднозначности.
Пример 2.1.4
Пусть в сигнатуре F={P}, R=Æ задана формула 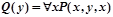 , задана интерпретация: M-множество целых чисел, φ(P)= {x, y, zÎM: x+y=z} - отношение между тремя целыми величинами, в котором сумма первых двух равна третьему. Тогда в данной интерпретации
, задана интерпретация: M-множество целых чисел, φ(P)= {x, y, zÎM: x+y=z} - отношение между тремя целыми величинами, в котором сумма первых двух равна третьему. Тогда в данной интерпретации 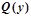 означает «y=0».
означает «y=0».
Вычислим значение 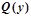 для различных y.
для различных y.
При y=1, 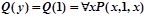 , задача сводится к вычислению истинностного значения формулы
, задача сводится к вычислению истинностного значения формулы 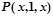 при различных целых значениях x, т.е. – истинностного значения предиката x+1=x. Из курса школьной алгебры известно, что данное равенство не выполняется ни при каких значениях x. Для наших целей достаточно, что данное равенство не выполняется хотя бы при одном значении x, например, при x=0. Отсюда следует, что
при различных целых значениях x, т.е. – истинностного значения предиката x+1=x. Из курса школьной алгебры известно, что данное равенство не выполняется ни при каких значениях x. Для наших целей достаточно, что данное равенство не выполняется хотя бы при одном значении x, например, при x=0. Отсюда следует, что 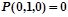 и значит
и значит 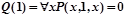 ,
,
При y=0, 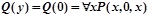 , задача сводится к вычислению истинностного значения формулы
, задача сводится к вычислению истинностного значения формулы 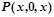 при различных целых значениях x, т.е. – истинностного значения предиката x+0=x. Из курса школьной алгебры известно, что данное равенство выполняется при всех значениях x. Отсюда следует, что
при различных целых значениях x, т.е. – истинностного значения предиката x+0=x. Из курса школьной алгебры известно, что данное равенство выполняется при всех значениях x. Отсюда следует, что 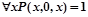 ,и значит
,и значит 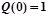 ,
,
Упражнение2.1.1
Что означают формулы в интерпретации примера 2.1.4?
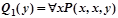 ,
,
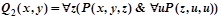
Вычислите истинностные значения при различных значениях свободных переменных.
Пример 2.1.5
Доказать, что формулы F=XÉY и G=XvY равносильны.
Для доказательства нужно составить таблицы истинности формул F и G (см. табл. 2.1.2).
Таблица 2.1.2
| X | Y | F=XÉY | X | G=XvY |
Столбцы, соответствующие формулам F и G одинаковые, значит формулы F и G равносильны, ч. т. д.
Упражнение2.1.2
Доказать, что следующие формулы логики высказываний равносильны (см. табл. 2.1.3):
Таблица 2.1.3
| F&1 º F; | |
| Fv1 º 1; | |
| F&0 º 0; | |
| Fv0 º F; | |
| F&F º F; | идемпотентность |
| FvF º F; | идемпотентность |
| F&G º G&F; | коммутативность |
| FvG º GvF; | коммутативность |
| F&(G&H) º (F&G)&H; | ассоциативность |
| Fv(GvH) º (FvG)vH; | ассоциативность |
| F&(GvH) º (F&G)v(F&H); | дистрибутивность |
| Fv(G&H) º (FvG)&(FvH); | дистрибутивность |
| F&(FvG) º F; | закон поглощения |
| Fv(F&G) º F; | закон поглощения |
| F&F º 0; | противоречие |
| FvF º 1; | правило исключенного третьего |
| (F&G) º FvG; | правило де Моргана |
| (FvG) º F&G; | правило де Моргана |
| F º F; | снятие двойного отрицания |
| FÉG º FvG; | |
| F~G º (FÉG)&(GÉF). |
На основе формул (табл. 2.1.3) можно производить доказательства равносильности двух формул посредством тождественных преобразований без построения таблиц истинности.
Пример 2.1.6
Доказать равносильность формул F и G:
F=(X&(ZÉY))v((XÉZ)&Y);
G=(XvY)&(YvZ).
Решение:
По формуле 20.
F=(X&(ZÉY))v((XÉZ)&Y) º (X&(ZvY))v((XvZ)&Y) º
по формулам 9, 10, 11,.
º (XvXvZ)&(ZvYvXvZ)&(XvY)&(ZvYvY) º
по формулам 16, 8,.
º (1vZ)&(1vYvX)&(XvY)&(ZvYvY) º
по формулам 2,.1,
º1&1&(XvY)&(ZvYvY) º (XvY)&(ZvYvY) º
по формулам 6, 8,.
º (XvY)&(ZvY) º (XvY)&(YvZ)=G ч. т. д.
Определение 2.1.7.Литерой будем называли высказывательную переменную (положительная литера) или ее отрицание (отрицательная литера), элементарной дизъюнкцией или дизъюнктом – дизъюнкцию литер или одиночную литеру, конъюнктивной нормальной формой или кнф– конъюнкцию дизъюнктов.
Теорема 1. Любая формула логики высказываний равносильна некоторой кнф.
Следствие1. Любая формула логики высказываний может быть тождественными преобразованиями приведена к кнф.
Пример 2.1.7
Доказать, что формула F=X&YÉX является тождественно истинной.
Для доказательства нужно составить таблицу истинности формулы F (см. табл. 1.4).
Таблица 1.4
| X | Y | X&Y | F=X&YÉX |
Столбец, соответствующий формуле F, содержит только значения 1, значит формула F=X&YÉX тождественно истина, ч. т. д.
Упражнение 2.1.3
Доказать, что формулы F и G равносильны тогда и только тогда, когда формула F~G является тождественно истинной.
Пример 2.1.8
Доказать, что формулы  и
и  равносильны.
равносильны.
Пусть φ - некоторая интерпретация, aÎМ. Пусть F(a)=1. Значит 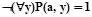 и
и 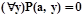 Следовательно, найдется bÎM, для которого
Следовательно, найдется bÎM, для которого 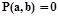 (в противном случае выполнялось бы равенство
(в противном случае выполнялось бы равенство 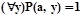 ). Если
). Если 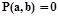 то
то 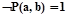 и, следовательно,
и, следовательно, 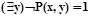 и
и 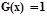 ,, Обратное утверждение доказывается аналогично. Следовательно, формулы F(x) и G(x) равносильны, ч. т. д.
,, Обратное утверждение доказывается аналогично. Следовательно, формулы F(x) и G(x) равносильны, ч. т. д.
Упражнение2.1.4
Доказать, что следующие формулы логики предикатов равносильны (см. табл. 2.1.4):
Таблица 2.1.4
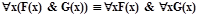
| вынос квантора всеобщности из конъюнкции |
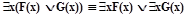
| вынос квантора существования из дизъюнкции |
| KxF(x)ºKzF(z) | переименование связанных переменных, KÎ{ 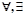 }. }.
|
| K1xK2z(F(x)·G(z))ºK1xF(x)·K2zG(z) | общий случай выноса квантора за скобки, здесь
K1, K2Î{ 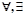 },·Î{&, V}. },·Î{&, V}.
|
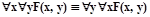
| перестановка одноименных кванторов |
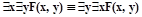
| перестановка одноименных кванторов |

| перенос квантора через отрицание |
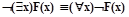
| перенос квантора через отрицание |
Упражнение2.1.5
Проверить равносильность следующих пар формул:
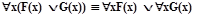
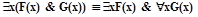
В логике первого порядка способ доказательства равносильности посредством тождественных преобразований является основным. Он может также использоваться для преобразования формул к тому или иному виду, что будет использовано в дальнейшем.
Определение 2.1.10.Литерой будем называли атомарную формулу (положительная литера) или ее отрицание (отрицательная литера), элементарной дизъюнкцией или дизъюнктом – дизъюнкцию литер или одиночную литеру, конъюнктивной нормальной формой или кнф– конъюнкцию дизъюнктов.
Теорема 2. Любая формула логики предикатов может быть тождественными преобразованиями приведена к виду (Q1x1)(Q2x2)… (Qnxn)F(x1 , x2,…, xn, y1 , y2,…, yn), где Q1, Q2,…, Qn – кванторы, связывающие переменные x1 , x2,…, xn, а F(x1 , x2,…, xn, y1, y2,…, yn) – формула логики предикатов, не содержащая кванторов, y2,…, yn – свободные переменные.
Пример 2.1.9
 ,
, 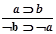 -известно, что эти рассуждения – верные.
-известно, что эти рассуждения – верные.
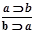 -,
-, 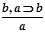 - -неверные рассуждения.
- -неверные рассуждения.
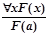 --верное рассуждение.
--верное рассуждение.
 -- неверное рассуждение.
-- неверное рассуждение.
Определение 2.1.13. Рассуждение 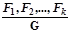 называется верным (формула G в этом случае называется логическим следствием формул F1,F2,…,Fk,), если для любой интерпретации φ (в логике предикатов, дополнительно, - для любых значений свободных переменных), для которой выполняются условия φ(F1)=φ(F2)=…=φ(Fk)=1, выполняется также φ(G)=1.
называется верным (формула G в этом случае называется логическим следствием формул F1,F2,…,Fk,), если для любой интерпретации φ (в логике предикатов, дополнительно, - для любых значений свободных переменных), для которой выполняются условия φ(F1)=φ(F2)=…=φ(Fk)=1, выполняется также φ(G)=1.
Упражнение 2.1.7
Доказать, что рассуждение 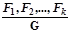 верно тогда и только тогда, когда формула F1&F2&…&Fk,ÉG является тождественно истинной (общезначимой).
верно тогда и только тогда, когда формула F1&F2&…&Fk,ÉG является тождественно истинной (общезначимой).
Упражнение 2.1.8
Доказать, что рассуждение 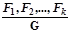 верно тогда и только тогда, когда формула F1&F2&…&Fk, &ØG является невыполнимой (противоречивой).
верно тогда и только тогда, когда формула F1&F2&…&Fk, &ØG является невыполнимой (противоречивой).
2.2. Метод резолюций
Назначение метода резолюций - доказательство того, что формула G является логическим следствием формул F1,F2,...,Fk. В основе метода лежит доказательство невыполнимости формулы F1&F2&…&Fk&ØG. Рассматриваемая формула приводится к кнф и кнф рассматривается как множество дизъюнктов. Дизъюнкт же может представляться, как множество литер.
Упражнение 2.2.1
Доказать правильность рассуждения 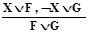 .
.
Пример 2.2.1
Исходные дизъюнкты: XvYvZ, XvY. По правилу резолюций выводим дизъюнкты:
YvZvY (контрарные литеры X и X)
XvZvX (контрарные литеры Y и Y).
Если исходные дизъюнкты X и X, из этой пары выводим дизъюнкт, не содержащий ни одной литеры. Будем называть его пустым и обозначать знаком «□». Пустой дизъюнкт равносилен значению 0. Значит F&□º□ и Fv□ ºF.
Определение 2.2.3. Пусть S – множество дизъюнктов. Выводом из S называется последовательность дизъюнктов
D,D2,...,Dn
такая, что каждый дизъюнкт этой последовательности принадлежит S или следует из предыдущих по правилу резолюций. Дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.
Пример 2.2.2
Исходное множество дизъюнктов: S={XvYvZ, YvU, X}. Рассмотрим последовательность:
D1=XvYvZ, D1ÎS.
D2=YvU, D2ÎS.
D3=XvZvU, следует из D1, D2 по правилу резолюций.
D4=X, D4ÎS.
D5=ZvU, следует из D3, D4 по правилу резолюций.
Рассматриваемая последовательность является выводом из S и дизъюнкт ZvU выводим из S.
Применение метода резолюций основано на следующей теореме.
Теорема 3. Множество дизъюнктов логики высказываний S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.
Пример 2.2.3
Докажем, что формула G=Z является логическим следствием формул F1=XvYÉX&Z, F2=YÉZ. Для этого нужно доказать невыполнимость формулы F1&F2&Gº (XvYÉX&Z)&(YÉZ)&Z. Приведем ее к кнф.
(XvYÉX&Z)&(YÉZ)&Zº((XvY)v(X&Z))&(YvZ)&Zº((X&Y)v(X&Z))&(YvZ)&Zº(X&(YvZ))&(YvZ)&ZºX&(YvZ)&(YvZ)&Z
Тогда исходное множество дизъюнктов S={X, YvZ, YvZ, Z}. Вывод пустого дизъюнкта:
D1=YvZ, D1ÎS.
D2=Z, D2ÎS.
D3=Y, следует из D1, D2 по правилу резолюций.
D4=YvZ, D4ÎS.
D5=У, следует из D2, D4 по правилу резолюций.
D6=□.
Пустой дизъюнкт выводим из S, следовательно, формула G является логическим следствием формул F1, и F2, ч. т. д.
2.2.2. Подстановка и унификация
Формулы логики предикатов содержат переменны, поэтому для сопоставления литер необходимо осуществлять подстановки вместо переменных их значений.
Определение 2.2.4. Подстановкой называется множество подстановочных компонент вида
s={x1=t1, x2=t2,…, xn=tn},
где x1,x2,…,xn – различные переменные, t1,t2,…,tn – термы, причем терм ti не содержит переменной xi (1≤ i ≤ n).
Если σ = (x1=t1,...,xn=tn) – подстановка, а F – некоторый объект логики предикатов (терм, дизъюнкт, формула, множество объектов и т. д.), то через σ(F) будем обозначать дизъюнкт, полученный из F одновременной заменой всех xi на ti,.
Пример 2.2.4.
если σ={x=f(y), y=c, z=g(u)), F=R(x, y, z)vP(f(y)), то σ(F)=R(f(y), c, g(u))vP(f(c).
Определение 2.2.5. Пусть {E1,…,Ek} – множество объектов логики предикатов. Подстановка σ называется унификатором этого множества, если σ(E1)=σ(E2)=…=σ(Ek). Множество унифицируемо, если существует унификатор этого множества.
Пример 2.2.5.
Множество атомарных формул {Q(a,x,f(x)), Q(u,у,z)} унифицируемо подстановкой {u=a, x=у, z=f(у)},
а множество {R(x,f(x)), R(u,u)} неунифицируемо.
Если множество унифицируемо, то существует, как правило, не один унификатор этого множества, а несколько. Среди всех унификаторов данного множества выделяют так называемый наиболее общий унификатор.
Определение 2.2.6. Пусть ξ и η – две подстановки. Тогда произведением (композицией) подстановок ξ и η (η◦ξ) называется подстановка z такая, что для любого объекта E выполняется равенство z(E)=η(ξ(E)).
Будем конструировать подстановку z следующим образом:
Алгоритм 1. Конструирование композиции подстановок.
Вход: подстановки ξ={x1=t1, x2=t2,…, xk=tk} и η={y1=s1, y2=s2,…, yl=sl}
1) получим из подстановок η и ξ множество подстановочных компонент {x1=η(t1), x2=η(t2),…,xk=η(tk), y1=s1, y2=s2,…, yl=sl},
2) удалим из него компоненты вида xi=xi для, если таковые найдутся для 1≤ i≤ k,
3) удалим компоненты вида yj=sj, если yj Î{x1,…, xk}, для 1≤j≤l, получим подстановку z=η◦ξ.
Пример 2.2.6
Рассмотрим пример. Пусть ξ = {x=f(y), z=y, u=g(d)}, η = {x=c, y=z}.
1) {x=f(y), z=z, u=g(d), x=c, y=z}.
2) {x=f(y), u=g(d), x=c, y=z}.
3) η◦ξ = {x=f(y), u=g(d), y=z}.
Упражнение 2.2.2.
Доказать, что результатом алгоритма 1 является композиция подстановок, удовлетворяющая определению 2.2.6.
Упражнение 2.2.3.
Доказать, что композиция подстановок ассоциативно, т.е. для любых подстановок ξ, η, ζ выполняется равенство ξ◦(η◦ζ)=(ξ◦η)◦ζ.
Введем пустую подстановку – подстановку, не содержащую подстановочных компонент. Будем обозначать ее через ε.
Упражнение 2.2.4.
Доказать, что пустая подстановка является единицей относительно умножения, т.е. для любой подстановки σ выполняются равенства σ◦ε=ε◦σ=σ.
Определение 2.2.7. Унификатор σ называется наиболее общим унификатором (НОУ), если для любого унификатора τ того же множества существует подстановка ξ такая, что τ=ξ○σ.
Пример 2.2.7
Для множества {P(x,f(а), g(z)), P(f(b),y,v)} наиболее общим унификатором является подстановка σ={x=f(b), y=f(a), v=g(z)}. Подстановка τ={x=f(b), y=f(a), z=c, v=g(c)}, то ξ={z=c} также является его унификатором. Однако τ=ξ○σ где ξ={z=c}.
Для изложения алгоритма нахождения наиболее общего унификатора потребуется понятие множества рассогласований в множестве объектов. Множество рассогласований строится следующим образом.
Алгоритм 2. Построение множества рассогласований.
Вход: множество объектов логики предикатов М, каждый объект представляет собой последовательность символов.
1) выделим первую слева позицию (позицию рассогласований), в которой не для всех объектов стоят одинаковые символы.
2) в каждом объекте выпишем подобъект, которое начинается с данной позиции (этими подобъектами могут быть литера, атомарная формула, терм).
3) множество полученных подобъектов называется множеством рассогласований в М.
Пример 2.2.8.
M={P(x, f(y), a), P(x,u, g(y)), P(x, c, v)}, позиция рассогласований – пятая, множество рассогласований - {f(y), u, c}.
M={P(x, y), P(a, g(z))}, позиция рассогласований – первая, множество рассогласований - {P(x, y), P(a, g(z))}.
M={P(x, y),Q(a, v)}, позиция рассогласований – вторая, множество рассогласований - {P(x, y), Q(a, v)}.
Алгоритм 3. Алгоритм унификации.
Вход: множество литер М, каждая литера представляет собой последовательность символов.
1) Положить k=0, Mk=M, σk=ε.
2) Если множество Мk состоит из одной литеры, то выдать σk в качестве НОУ, завершить работу иначе найти множество Nk рассогласований в Mk.
3) Если в множестве Nk существует переменная vk и терм tk, не содержащий vk, то перейти к шагу 4, иначе множество М неунифицируемо, завершить работу.
4) Положить σk+1={vk,=tk}○σk,. К множеству Mk применить подстановку vk=tk, полученное множество литер взять в качестве Mk+1.
5) Положить k=k+1 и перейти к шагу 2.
Пример 2.2.9.Проиллюстрируем работу алгоритма унификации на множестве М.
М={P(x,f(y)), P(a,u)}.
· 1). k=0, σ0=ε, M0=M,
· 2). N0={x,a},
· 3)-4). σ1={x=a}, M1={P(a,f(y)),P(a,u)},
· 5). k=1,
· 2). N1={f(y), u},
· 3)-4). σ2={x=a, u=f(y)}, M2={P(a,f(u))},
· 5). k=2,
· 2). НОУ={x=a, u=f(y)}. Конец работы.
M={P(x,f(y)), P(a,b)}.
· 1). k=0, σ0=ε, M0=M,
· 2). N0={x,a},
· 3)-4). σ1={x=a}, M1={P(a,f(y)), P(a,b)},
· 5). k=1,
· 2). N1={f(y), b},
· 3) М неунифицируемо. Конец работы.
Упражнение 2.2.5.
Доказать, что алгоритм 3 правильно (в соответствии с определениями) оценивает унифицируемость множества литер и находит НОУ.
Пример 2.2.10.
Исходные дизъюнкты: Q(a,f(x))vR(x), Q(u,z)vP(z). По правилу резолюций выводим дизъюнкт:
R(x)vP(f(x)) (отрезаемые литеры - Q(a,f(x)), Q(u,z), НОУ σ={u=a, z=f(x)}
В отличие от логики высказываний, в логике предикатов нам понадобится еще одно правило.
Определение 2.2.9. Правилом склейки в логике предикатов называется правило:
из дизъюнкта ◊P(t1,...,tn)v...v◊P(s1,...,sn)vF выводим дизъюнкт σ (◊P(t1,...,tn)vσ(F),
где σ – наиболее общий унификатор множества {P(t1,...,tn),...,P(s1,...,sn)},
◊ – знак отрицания или его отсутствие.
Дизъюнкт σ(◊P(t1,…,tn)vσ(F) называется склейкой первого дизъюнкта.
Пример 2.2.11.
Исходный дизъюнкт: Р(х,у)vP(у,х)vР(а,а)vQ(x,y,v), по правилу склейки дает дизъюнкт Р(а,а)vQ(a,a,v).
НОУ - σ={х=a, у =a }.
Определение вывода в логике первого порядка немного отличается от аналогичного определения в логике высказываний.
Определение2.2.12. Пусть S – множество дизъюнктов. Выводом из множества дизъюнктов S называется последовательность дизъюнктов
D1,D2,…,Dn,
такая, что каждый дизъюнкт Di принадлежит S, выводим из предыдущих дизъюнктов по правилу резолюций или выводим из предыдущего по правилу склейки.
Как и в логике высказываний, дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.
Пример 2.2.12.
Исходное множество дизъюнктов: S={B(x)vC(x)vT(f(x)), C(у)vT(f(z)), B(a)}. Рассмотрим последовательность:
D1=B(x)vC(x)vT(f(x)), D1ÎS.
D2=C(у)vT(f(z)), D2ÎS.
D3=B(x)vT(f(x))vT(f(z)), бинарная резольвента дизъюнктов D1, D2, НОУ - σ={у = х}.
D4=B(x)vT(f(x)), из D3 по правилу склейки, НОУ - σ={z = х}.
D5=B(a), D5ÎS.
D6=T(f(a)), бинарная резольвента дизъюнктов D4, D5, НОУ - σ={ х = a }.
Рассматриваемая последовательность является выводом из S.
Теорема 4. Множество дизъюнктов S логики первого порядка невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.
Метод резолюций для доказательства следования формулы G из формул F1,…,Fk мож
Дата: 2016-10-02, просмотров: 300.