Сформулируем правила порождения дизъюнктов для логики первого порядка.
Определение 2.2.8. Правилом резолюций в логике предикатов называется следующее правило
из дизъюнктов P(t1,...,tn)vF и P(s1,...,sn)vG выводим дизъюнкт σ(F)vσ(G),
где σ – наиболее общий унификатор множества {P(t1,...,tn), P(s1,...,sn)}.
Дизъюнкт σ(F)vσ(G) называется бинарной револьвентой двух дизъюнктов, а литеры P(t1,…,tn) и P(s1,…,sn) отрезаемыми литерами.
Пример 2.2.10.
Исходные дизъюнкты: Q(a,f(x))vR(x), Q(u,z)vP(z). По правилу резолюций выводим дизъюнкт:
R(x)vP(f(x)) (отрезаемые литеры - Q(a,f(x)), Q(u,z), НОУ σ={u=a, z=f(x)}
В отличие от логики высказываний, в логике предикатов нам понадобится еще одно правило.
Определение 2.2.9. Правилом склейки в логике предикатов называется правило:
из дизъюнкта ◊P(t1,...,tn)v...v◊P(s1,...,sn)vF выводим дизъюнкт σ (◊P(t1,...,tn)vσ(F),
где σ – наиболее общий унификатор множества {P(t1,...,tn),...,P(s1,...,sn)},
◊ – знак отрицания или его отсутствие.
Дизъюнкт σ(◊P(t1,…,tn)vσ(F) называется склейкой первого дизъюнкта.
Пример 2.2.11.
Исходный дизъюнкт: Р(х,у)vP(у,х)vР(а,а)vQ(x,y,v), по правилу склейки дает дизъюнкт Р(а,а)vQ(a,a,v).
НОУ - σ={х=a, у =a }.
Определение вывода в логике первого порядка немного отличается от аналогичного определения в логике высказываний.
Определение2.2.12. Пусть S – множество дизъюнктов. Выводом из множества дизъюнктов S называется последовательность дизъюнктов
D1,D2,…,Dn,
такая, что каждый дизъюнкт Di принадлежит S, выводим из предыдущих дизъюнктов по правилу резолюций или выводим из предыдущего по правилу склейки.
Как и в логике высказываний, дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.
Пример 2.2.12.
Исходное множество дизъюнктов: S={B(x)vC(x)vT(f(x)), C(у)vT(f(z)), B(a)}. Рассмотрим последовательность:
D1=B(x)vC(x)vT(f(x)), D1ÎS.
D2=C(у)vT(f(z)), D2ÎS.
D3=B(x)vT(f(x))vT(f(z)), бинарная резольвента дизъюнктов D1, D2, НОУ - σ={у = х}.
D4=B(x)vT(f(x)), из D3 по правилу склейки, НОУ - σ={z = х}.
D5=B(a), D5ÎS.
D6=T(f(a)), бинарная резольвента дизъюнктов D4, D5, НОУ - σ={ х = a }.
Рассматриваемая последовательность является выводом из S.
Теорема 4. Множество дизъюнктов S логики первого порядка невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.
Метод резолюций для доказательства следования формулы G из формул F1,…,Fk может применяться лишь в случае, когда формулы F1,…, Fk и G не имеют свободных переменных.
Вопрос:Можно ли сформулировать содержательное утверждение, которое записывается формулой логики предикатов в некоторой интерпретации?
Метод резолюций в логике предикатов применяется в следующей последовательности шагов:
1) записывается формула логики предикатов F1&F2&…&Fk, &ØG;
2) формула приводится к виду (Q1x1)(Q2x2)… (Qnxn)F(x1 , x2,…, xn) по теореме 2 при отсутствии свободных переменных;
3) удаляются кванторы существования, для этого подформулу вида  . заменяется на
. заменяется на 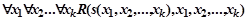 , где s – новый функциональный символ, не входящий до этого в сигнатуру, s – называется функцией Сколема;
, где s – новый функциональный символ, не входящий до этого в сигнатуру, s – называется функцией Сколема;
4) удаляются кванторы всеобщности;
5) оставшаяся бескванторная формула приводится к кнф, которая рассматривается как множество дизъюнктов;
6) выводится пустой дизъюнкт.
Пример 2.2.13.
Докажем, что формула G является логическим следствием множества формул F1,F2.
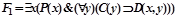 ,
,
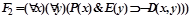 ,
,
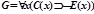 .
.
Будем следовать описанной последовательности шагов.
1) записывается формула логики предикатов F1&F2&ØG;
2) преобразуем отдельно F1, F2,ØG
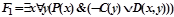 ,
,
 ,
,
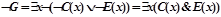 ;
;
3) удаляются кванторы существования, a, b-сколемовские константы,
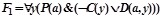 ,
,
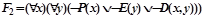 ,
,
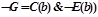 ;
;
4) удаляются кванторы всеобщности
 ,
,
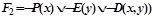 ,
,
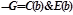 ;
;
5) оставшаяся бескванторная формула приводится к кнф 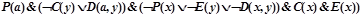 , которая рассматривается как множество дизъюнктов S=
, которая рассматривается как множество дизъюнктов S= 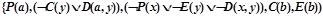 ;
;
6) выводится пустой дизъюнкт
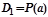 ÎS;
ÎS;
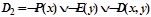 ÎS;
ÎS;
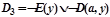 , бинарная резольвента дизъюнктов D1, D2, НОУ - σ={х = a};
, бинарная резольвента дизъюнктов D1, D2, НОУ - σ={х = a};
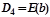 ÎS;
ÎS;
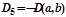 , бинарная резольвента дизъюнктов D3, D4, НОУ - σ={y = b};
, бинарная резольвента дизъюнктов D3, D4, НОУ - σ={y = b};
 ÎS;
ÎS;
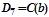 ÎS;
ÎS;
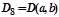 - бинарная резольвента дизъюнктов D6, D7, НОУ - σ={y = b};
- бинарная резольвента дизъюнктов D6, D7, НОУ - σ={y = b};
D9 = □ - бинарная резольвента дизъюнктов D5, D8, НОУ - e;
2.2.4. Стратегии метода резолюций
До сих пор для доказательства противоречивости формулы мы приводили соответствующий вывод пустого дизъюнкта. Однако, основная и наиболее сложная проблема метода резолюций – найти этот вывод. В множестве дизъюнктов существует, как правило, не одна пара дизъюнктов и не одна пара контрарных литер, к которым можно применить правило резолюций. Способ выбора дизъюнктов и литер в них, для применения правил резолюции (и склейки), называется стратегией метода.
Алгоритм 4. Стратегия насыщения уровней (перебор вширь, полный перебор).
Вход: S – исходное упорядоченное множество дизъюнктов.
1) S0=S, n=0.
2) для n>0, если получены последовательности дизъюнктов S0, S1,…,Sn-1, последовательность Sn будет состоять из всевозможных резольвент дизъюнктов D1 и D2, где в качестве D2 берутся по порядку дизъюнкты из Sn-1, а в качестве D1 – дизъюнкты из S0,S1,…,Sn-1, предшествующие D2.
Пример 2.2.14.
S={XvY, XvY, XvZ, XvZ, Z}:
| S0: | XvY, | |||
| XvY, | ||||
| XvZ, | ||||
| XvZ, | ||||
| Z, | ||||
| S1: | YvY, | из (1) и (2), | т. истин. | |
| XvX, | из (1) и (2), | т. истин. | ||
| YvZ, | из (2) и (3), | |||
| YvZ, | из (1) и (4), | |||
| Z, | из (3) и (4), | |||
| X, | из (3) и (5), | |||
| X, | из (4) и (5) | |||
| S2: | XvY, | из (1) и (6), | уже был | |
| XvY, | из (2) и (6), | уже был | ||
| XvY, | из (1) и (7), | уже был | ||
| XvY, | из (2) и (7), | уже был | ||
| XvZ, | из (3) и (7), | уже был | ||
| XvZ, | из (4) и (7), | уже был | ||
| XvZ, | из (1) и (8), | уже был | ||
| YvZ, | из (6) и (8), | уже был | ||
| XvZ, | из (2) и (9), | уже был | ||
| YvZ, | из (6) и (9), | уже был | ||
| Z, | из (8) и (9), | уже был | ||
| □. | из (5) и (10). |
Мы видим, что порождено много лишних дизъюнктов. Удаление тождественно истинного дизъюнкта не влияет на выполнимость множества дизъюнктов. Некоторые дизъюнкты порождаются неоднократно. Их также можно удалить. В общем случае можно вычеркивать из вывода дизъюнкты, являющиеся расширениями уже имеющихся в выводе дизъюнктов.
Определение 2.2.13. Дизъюнкт D называется расширением дизъюнкта C, если существует подстановка σ такая, что σ(C)vQ =D.
Для логики высказываний это означает, что D=CvQ. Для логики предикатов приведем пример.
Пример 2.2.15.
D=Q(a)vP(b,y)vR(u) есть расширение дизъюнкта C=P(x,y)vQ(z)vQ(v).
Подстановка σ={x=b, z=a, v=a)}.
Пример 2.2.16.
Стратегия насыщения уровней с удалением лишних дизъюнктов дает более короткий вывод для примера.2.2.14.
| S0: | XvY, | ||
| XvY, | |||
| XvZ, | |||
| XvZ, | |||
| Z, | |||
| S1: | YvZ, | из (2) и (3), | |
| YvZ, | из (1) и (4), | ||
| Z, | из (3) и (4), | ||
| X, | из (3) и (5), | ||
| X, | из (4) и (5) | ||
| S2: | □. | из (5) и (8). |
Рассмотренные стратегии являются полными в том смысле, что если множество дизъюнктов S невыполнимо, то из S пользуясь стратегией можно вывести пустой дизъюнкт.
Упражнение 2.2.6.
Доказать полноту стратегии полного перебора.
Упражнение 2.2.7.
Доказать полноту стратегии вычеркивания.
Указание: если D–расширение C, то DvCºC. Воспользоваться результатом упражнения 2.2.6
Определение 2.2.14. Револьвентой дизъюнктов D1 и D2 называется одна из следующих бинарных револьвент:
1) бинарная револьвента дизъюнктов D1 и D2,
2) бинарная револьвента склейки D1 и дизъюнкта D2,
3) бинарная револьвента дизъюнкта D1 и склейки D2,
4) бинарная револьвента склейки D1 и склейки D2.
Определение 2.2.15. (Другое определение револьвенты):
пусть D1и D2 -дизъюнкты - множества литер и d1ÎD1и d2ÎD2 -подмножества литер,
пусть σ - наиболее общий унификатор множества d1ßd2 (d2 - множество литер, полученное из d2 –путем добавления отрицания к каждой литере, если она положительная, или снятия отрицания, если она отрицательная)
тогда револьвентой дизъюнктов D1 и D2 называется дизъюнкт - множества литер σ((D1\d1)ß(D2\d2)).
Пример 2.2.17.
Исходные дизъюнкты: Q(a,f(x))vQ(a,f(y))vR(x), Q(u,z)vP(z). Т.е. D1={Q(a,f(x)), Q(a,f(y)), R(x)}, D2={Q(u,z),P(z)}
Выводим револьвенты:
Q(a,f(y))vR(x)vP(f(x)) (d1={Q(a,f(x)) }, d2={Q(u,z) }, НОУ σ={u=a, z=f(x)}
Q(a,f(x))vR(x)vP(f(y)) (d1={Q(a,f(y)) }, d2={Q(u,z) }, НОУ σ={u=a, z=f(y)}
R(x)vP(f(x)) (d1={Q(a,f(x)), Q(a,f(y)) }, d2={Q(u,z) }, НОУ σ={u=a, z=f(x), y=x}
Упражнение 2.2.8.
Исходные дизъюнкты: Q(a,f(x))v Q(a,f(y))v R(x), Q(u,f(x))vQ(u,z)vP(z). Сколько револьвент можно вывести? Найдите эти револьвенты.
Упражнение 2.2.9.
Доказать, что определения резольвенты 2.2.14 и 2.2.15 эквивалентны.
Алгоритм 5. Стратегия перебора в глубину.
Вход: S – исходное упорядоченное множество дизъюнктов, в каждом дизъюнкте литеры также упорядочены. Если из двух дизъюнктов выводимы несколько резольвент, то эти резольвенты также упорядочены.
1) в качестве D1 берется последний дизъюнкт из S.
2) в качестве D2 берется первый дизъюнкт из S.
3) пока нет резольвент D1 и D2 и множество S не исчерпано выбирать в качестве D2 следующий по порядку дизъюнкт из S.
4) если множество S исчерпано, то ВЫХОД(неудача)
5) если есть резольвенты D1 и D2, то взять первую по порядку
6) если взятая резольвента – пустой дизъюнкт, то КОНЕЦ РАБОТЫ(успех).
7) если взятая резольвента – не пустой дизъюнкт и ее еще не было, то поместить ее в конец множества S, получить множество S1.
8) применить описываемый алгоритм рекурсивно к множеству S1.
9) если есть еще резольвенты D1 и D2, то взять следующую по порядку резольвенту D1 и D2, перейти к п. 6).
10) если нет больше резольвент D1 и D2, то перейти к п. 3).
Пример 2.2.17.
Стратегия перебора в глубину дает следующий вывод для примера.2.2.14.
| XvY, | ||||
| XvY, | ||||
| XvZ, | ||||
| XvZ, | ||||
| Z, | ||||
| X, | из (5) и (3), | рекурсивный вызов | ||
| Y, | из (6) и (2), | рекурсивный вызов | ||
| X, | из (7) и (1), | уже был | возврат к шагу 7 | |
| Y, | возврат, | резольвент нет | возврат к шагу 6 | |
| X, | возврат, | |||
| Z, | из (6) и (4), | рекурсивный вызов | ||
| □. | из (7) и (5) | КОНЕЦ РАБОТЫ (успех) |
2.3. Отношения и предикаты
Определение 2.3.1. Прямым произведением множеств A1,…, An (обозначается как A1´…´An.) в теории множеств называется множество {(a1,…,an): a1,Î A1,,…,anÎ An}.
Определение 2.3.2. Отношением между множествами A1,…, An называется некоторое множество RÍ A1´…´An.
Определение 2.3.3. n-арным отношением на множестве A называется некоторое множество RÍ An. (An=A´A´…´A – прямое произведение A на само себя n раз)
Определение 2.3.4. Сечением отношения RÍ A1´…´An по компоненте i и значению c называется отношение R1={(a1,…, ai-1 ,ai+1 ,.., an): (a1,…, ai-1,c,ai+1 ,.., an)ÎR }.
Пусть М – некоторое множество значений переменных.
Предикат P(x1,…,xn) можно представить в виде функции p: М n→{0,1} от n переменных, которая при заданных аргументах принимает значения в зависимости от истинности полученного высказывания.
Предикат P(x1,…,xn) можно представить в виде отношения на множестве M следующим образом:
P ={(a1,…,an)ÎMn : высказывание P(a1,…,an) истинно} или
P ={(a1,…,an)ÎMn : P(a1,…,an)=1}.
Дата: 2016-10-02, просмотров: 395.