Определение 2.1.4. Интерпретацией называется функция

φ:A→{0,1},

где А – множество высказывательных переменных, такая, что φ(0)=0, φ(1)=1.

Интерпретацию можно расширить на множество всех формул, используя следующие таблицы истинности логических связок (см. табл. 2.1.1).

Таблица 2.1.1

Пример 2.1.3

Пусть φ(X)=1, φ(Y)=0, φ(Z)=1, F=XvYÉZ, G=X&Y~Y&Z.

Тогда φ(F)=1, φ(G)=0.

При указании истинностных значений формул будем опускать символ интерпретации, т. е. вместо φ(F)=1, φ(G)=0 будем писать просто F=1, G=0, если это не приводит к неоднозначности.

Интерпретация в логике предикатов первого порядка

Пусть заданы непустое множество М, характеризующее предметную область решаемой задачи, R – множество функций, определенных на множестве М, включающее:

§ функции, имеющие значения на множестве М;

§ функции, имеющие значения на множестве {0,1}, т. е предикаты;

§ местные функции (предметные константы);

§ местные предикаты (логические константы).

Обозначим через F – множество функциональных символов; P – множество предикатных символов, используемых при задании формулы. В дальнейшем объединение этих множеств FÈP будем называть сигнатурой формулы.

Определение 2.1.5. Интерпретацией называется функция φ: F ´P→ R, которая

1) константе ставит в соответствие элемент из М;

2) символу n-местной функции ставит в соответствие некоторую n-местную функцию, определенную на множестве М;

3) символу n-местного предиката ставит в соответствие n-местный предикат, заданный на М (n-местное отношение на М).

В результате, данная функция φ может быть применена к любой формуле F и φ(F) представляет собой предикат (отношение на множестве М), местность которого равна числу свободных переменных F.

Вычисление истинностного значения формулы логики предикатов сводится к следующим шагам::

q задать интерпретацию

q задать предметные значения свободных переменных

q вычислить значение терма

o если терм является предметной переменной или константой, то в качестве значения терма берется значение соответствующей переменной или константы

o если терм является выражением вида f(t₁,…,t_n), где t₁,…,t_n – термы, а f – n-местный функциональный символ, то в качестве значения терма берется результат применения функции φ(f) к ранее вычисленным значениям термов t₁,…,t_n.

q вычислить истинностноезначение атомарной формулы

o атомарной формулой является выражение вида P(t₁,…,t_n), где t₁,…,t_n – термы, P – символ n-местного предиката, в качестве истинностного значения атомарной формулы берется истинностноезначение высказывания, полученного подстановкой ранее вычисленных значений термов t₁,…, t_n.в предикат φ(P).

q вычислить истинностноезначение формулы логики первого порядка

o если формула логики первого порядка является атомарной формулой, то в качестве ее истинностного значения берется вычисленной истинностноезначение атомарной формулы

o если формула логики первого порядка является выражением вида (F)&(G), (F₁)v(G), (F), (F)É(G),(F) ~ (G), где F и G – формулы, значения которых уже вычислены, то требуемое истинностное значения вычисляется по таблицам истинности (см. табл. 2.1.1)

o если формула логики первого порядка является выражением вида 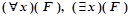, где F – формула логики предикатов, x – переменная, то истинностное значения вычисляется следующим образом:

§ x – единственная свободная переменная в формуле F, не получившая еще значения. В этом случае необходимо каким-либо образом ответить на вопрос, для всех ли значений переменной x формула F истина или ложна[1]

§ x - не входит в формулу F, значит формула F не содержит не получившая еще значения переменных и, следовательно, φ(F) представляет собой высказывание, истинностное значение которого и нужно выяснить

Пример 2.1.4

Пусть в сигнатуре F={P}, R=Æ задана формула 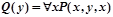, задана интерпретация: M-множество целых чисел, φ(P)= {x, y, zÎM: x+y=z} - отношение между тремя целыми величинами, в котором сумма первых двух равна третьему. Тогда в данной интерпретации 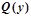означает «y=0».

Вычислим значение 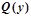для различных y.

При y=1, 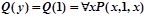, задача сводится к вычислению истинностного значения формулы 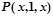при различных целых значениях x, т.е. – истинностного значения предиката x+1=x. Из курса школьной алгебры известно, что данное равенство не выполняется ни при каких значениях x. Для наших целей достаточно, что данное равенство не выполняется хотя бы при одном значении x, например, при x=0. Отсюда следует, что 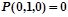и значит ,

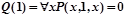При y=0, 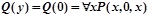, задача сводится к вычислению истинностного значения формулы 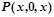при различных целых значениях x, т.е. – истинностного значения предиката x+0=x. Из курса школьной алгебры известно, что данное равенство выполняется при всех значениях x. Отсюда следует, что 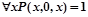,и значит ,

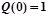Упражнение2.1.1

Что означают формулы в интерпретации примера 2.1.4?

,

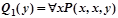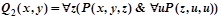
Вычислите истинностные значения при различных значениях свободных переменных.