Определение 2.1.6 Формулы F и G называются равносильными (FºG), если для любой интерпретации φ выполняется равенство φ(F)=φ(G).
Пример 2.1.5
Доказать, что формулы F=XÉY и G=XvY равносильны.
Для доказательства нужно составить таблицы истинности формул F и G (см. табл. 2.1.2).
Таблица 2.1.2
| X | Y | F=XÉY | X | G=XvY |
Столбцы, соответствующие формулам F и G одинаковые, значит формулы F и G равносильны, ч. т. д.
Упражнение2.1.2
Доказать, что следующие формулы логики высказываний равносильны (см. табл. 2.1.3):
Таблица 2.1.3
| F&1 º F; | |
| Fv1 º 1; | |
| F&0 º 0; | |
| Fv0 º F; | |
| F&F º F; | идемпотентность |
| FvF º F; | идемпотентность |
| F&G º G&F; | коммутативность |
| FvG º GvF; | коммутативность |
| F&(G&H) º (F&G)&H; | ассоциативность |
| Fv(GvH) º (FvG)vH; | ассоциативность |
| F&(GvH) º (F&G)v(F&H); | дистрибутивность |
| Fv(G&H) º (FvG)&(FvH); | дистрибутивность |
| F&(FvG) º F; | закон поглощения |
| Fv(F&G) º F; | закон поглощения |
| F&F º 0; | противоречие |
| FvF º 1; | правило исключенного третьего |
| (F&G) º FvG; | правило де Моргана |
| (FvG) º F&G; | правило де Моргана |
| F º F; | снятие двойного отрицания |
| FÉG º FvG; | |
| F~G º (FÉG)&(GÉF). |
На основе формул (табл. 2.1.3) можно производить доказательства равносильности двух формул посредством тождественных преобразований без построения таблиц истинности.
Пример 2.1.6
Доказать равносильность формул F и G:
F=(X&(ZÉY))v((XÉZ)&Y);
G=(XvY)&(YvZ).
Решение:
По формуле 20.
F=(X&(ZÉY))v((XÉZ)&Y) º (X&(ZvY))v((XvZ)&Y) º
по формулам 9, 10, 11,.
º (XvXvZ)&(ZvYvXvZ)&(XvY)&(ZvYvY) º
по формулам 16, 8,.
º (1vZ)&(1vYvX)&(XvY)&(ZvYvY) º
по формулам 2,.1,
º1&1&(XvY)&(ZvYvY) º (XvY)&(ZvYvY) º
по формулам 6, 8,.
º (XvY)&(ZvY) º (XvY)&(YvZ)=G ч. т. д.
Определение 2.1.7.Литерой будем называли высказывательную переменную (положительная литера) или ее отрицание (отрицательная литера), элементарной дизъюнкцией или дизъюнктом – дизъюнкцию литер или одиночную литеру, конъюнктивной нормальной формой или кнф– конъюнкцию дизъюнктов.
Теорема 1. Любая формула логики высказываний равносильна некоторой кнф.
Следствие1. Любая формула логики высказываний может быть тождественными преобразованиями приведена к кнф.
Тождественная истинность формул логики высказываний
Определение 2.1.8 Формула F называется тождественно истинной если для любой интерпретации φ выполняется равенство φ(F)=1.
Пример 2.1.7
Доказать, что формула F=X&YÉX является тождественно истинной.
Для доказательства нужно составить таблицу истинности формулы F (см. табл. 1.4).
Таблица 1.4
| X | Y | X&Y | F=X&YÉX |
Столбец, соответствующий формуле F, содержит только значения 1, значит формула F=X&YÉX тождественно истина, ч. т. д.
Упражнение 2.1.3
Доказать, что формулы F и G равносильны тогда и только тогда, когда формула F~G является тождественно истинной.
Равносильность формул логики первого порядка
Определение 2.1.9. Формулы F(x1,…,xn) и G(x1,…,xn) называются равносильными (F(x1,…,xn)ºG(x1,…,xn)), если для любой интерпретации φ при любых значениях свободных переменных x1=a1,…,xn=an истинностные значения высказываний φ(F(a1,…,an)) и φ(G(a1,…,an)) совпадают.
Пример 2.1.8
Доказать, что формулы  и
и  равносильны.
равносильны.
Пусть φ - некоторая интерпретация, aÎМ. Пусть F(a)=1. Значит 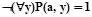 и
и 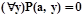 Следовательно, найдется bÎM, для которого
Следовательно, найдется bÎM, для которого 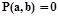 (в противном случае выполнялось бы равенство
(в противном случае выполнялось бы равенство 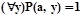 ). Если
). Если 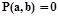 то
то 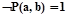 и, следовательно,
и, следовательно, 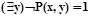 и
и 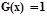 ,, Обратное утверждение доказывается аналогично. Следовательно, формулы F(x) и G(x) равносильны, ч. т. д.
,, Обратное утверждение доказывается аналогично. Следовательно, формулы F(x) и G(x) равносильны, ч. т. д.
Упражнение2.1.4
Доказать, что следующие формулы логики предикатов равносильны (см. табл. 2.1.4):
Таблица 2.1.4
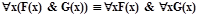
| вынос квантора всеобщности из конъюнкции |
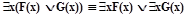
| вынос квантора существования из дизъюнкции |
| KxF(x)ºKzF(z) | переименование связанных переменных, KÎ{ 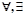 }. }.
|
| K1xK2z(F(x)·G(z))ºK1xF(x)·K2zG(z) | общий случай выноса квантора за скобки, здесь
K1, K2Î{ 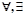 },·Î{&, V}. },·Î{&, V}.
|
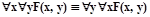
| перестановка одноименных кванторов |
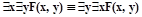
| перестановка одноименных кванторов |

| перенос квантора через отрицание |
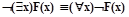
| перенос квантора через отрицание |
Упражнение2.1.5
Проверить равносильность следующих пар формул:
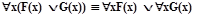
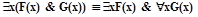
В логике первого порядка способ доказательства равносильности посредством тождественных преобразований является основным. Он может также использоваться для преобразования формул к тому или иному виду, что будет использовано в дальнейшем.
Определение 2.1.10.Литерой будем называли атомарную формулу (положительная литера) или ее отрицание (отрицательная литера), элементарной дизъюнкцией или дизъюнктом – дизъюнкцию литер или одиночную литеру, конъюнктивной нормальной формой или кнф– конъюнкцию дизъюнктов.
Теорема 2. Любая формула логики предикатов может быть тождественными преобразованиями приведена к виду (Q1x1)(Q2x2)… (Qnxn)F(x1 , x2,…, xn, y1 , y2,…, yn), где Q1, Q2,…, Qn – кванторы, связывающие переменные x1 , x2,…, xn, а F(x1 , x2,…, xn, y1, y2,…, yn) – формула логики предикатов, не содержащая кванторов, y2,…, yn – свободные переменные.
Дата: 2016-10-02, просмотров: 319.