обратите также внимание, как именно в формуле массива (3) заданы два условия в функции ЕСЛИ(). Дело в том, что эквивалентом логического значения ИСТИНА является 1, логического значения ЛОЖЬ является 0, таким образом, перемножение двух значений эквивалентно выполнения логической операции И (), то есть в качестве ответа выдается 1 (то есть ИСТИНА) в том, и только в том случае, если оба аргумента равны 1 (то есть ИСТИНА) и 0 — в любом другом случае. Более того, использование самой имеющейся в Excel логической функции И () в формуле массива выдает некорректный результат.
Построение формулы нахождения суммы четных отрицательных чисел диапазона. Обратите внимание, что условия в данном случае также два
- четность суммируемых чисел диапазона (то есть равенство 0 остатка от деления на 2) — ОСТАТ(A1:B4;2)=0;
- и то, что суммируемые числа — отрицательные — A1:B4<0;
Результирующая формула массива имеет вид:
{=СУММ(ЕСЛИ((ОСТАТ(A1:B4;2)=0)*(A1:B4<0);A1:B4;0))}
(для просмотра рекомендуется полноэкранный режим)
Возвращаясь к первоначальной задаче (найти сумму элементов диапазона из отрезка [-5;10]) — еще один возможный вариант формулы массивас задействованием вложенной функции ЕСЛИ() для того, чтобы задать второе условие (т.е. аналог (2)):
{=СУММ(ЕСЛИ(A1:B4>=-5;ЕСЛИ(A1:B4<=10;A1:B4;);))}
обратите внимание, что в этом случае для функции ЕСЛИ() вообще не заданы на соответствующих позициях значения, присваиваемые в том случае, если логическое условие не выполняется (в предыдущем случае задавались значения, равные 0) — возможный, хотя и, вероятно, менее «читаемый» вариант, чем (2).
Несколько дополнительных замечаний.
Не будет считаться ошибкой выполнения задания в несколько действий.
1. Например, сначала создается первый дополнительный диапазон, равный по размерности исходному A1:B4 (например, H1:I4), в который выводятся значения, удовлетворяющие первому критерию (т.е. большие либо равные -5) с помощью формулы
=ЕСЛИ(A1>=-5;A1;"")
(и аналогичных формул для остальных ячеек), затем — создается второй дополнительный диапазон той же размерности (например, K1:L4), в который, в свою очередь, выводятся значения предыдущего диапазона H1:I4, удовлетворяющие второму критерию (то есть меньшие либо равные 10) с помощью аналогочной предыдущей —
=ЕСЛИ(I1<=10;I1;"")
и, наконец, в свободную ячейку вводится формула для суммирования значений второго вспомогательного диапазона:
=СУММ(K1:L4)
2. Еще один вариант — создание только одного вспомогательного диапазона, опять же по размерности аналогичного исходному A1:B4 — например, M1:N4, в который выводятся значения исходного диапазона, удовлетворяющие обоим критериям с помощью формулы:
=ЕСЛИ(И(A1>=-5;<=10);A1;"")
в этом случае уже допустимо использование логической функции И(), а далее остается в свободную ячейку ввести суммирующую формулу —
=СУММ(M1:N4)
3. Наконец, еще один вариант решения данной задачи, уже упоминавшийся выше, состоит в использовании упомянутой функции СУММЕСЛИ(). Коль скоро вычисление суммы значений удовлетворяющих одному критерию функция позволяет, алгоритм решения состоит в том, чтобы снучала просуммировать все значения исходного диапазона, а затем вычесть из указанной суммы две суммы полученные с использованием функции СУММЕСЛИ() — первая — те значения, которые не удовлетворяют первому критерию (то есть меньшие -5), а вторая — те, которые не удовлетворяют второму (то есть большие 10):
=СУММ(A1:B4)-СУММЕСЛИ(A1:B4;"<-5")-СУММЕСЛИ(A1:B4;">10")
Еще один вариант — просуммировать те знаения, которые удовлетворяют первому критерию (то есть большие и равные -5) и те, которые удовлетворяют второму критерию (то есть меньшие и равные 10), в результате полученная сумма будет отличаться от суммы всех элементов диапазона как раз на требуемую сумму удовлетворяющих обоим критериям значений (значения большие и равные -5 и меньшие и равные 10 присутствуют и в первом и во втором слагаемом), и остается лишь отнять сумму всех значений:
=СУММЕСЛИ(A1:B4;">=-5")-СУММЕСЛИ(A1:B4;"<=10")-СУММ(A1:B4)
Лабораторная работа №10.
Логические переменные и функции.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1.Составьте электронную таблицу для решения уравнения вида
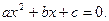
с анализом дискриминанта и коэффициентов a, b, c. Для обозначения коэффициентов, дискриминанта и корней уравнения применить имена.
Выполнение.
В ячейки A3, В3 и С3 введите значения коэффициентов квадратного уравнения и обозначьте эти ячейки именами a, b и с. Ячейку А4, где будет размещаться значение дискриминанта, обозначьте именем D. Для вычисления дискриминанта в ячейку А4 введите формулу =b^2-4*a*c_,затем для вычисления корней в ячейки А5 и А6 введите функцию ЕСЛИ с соответствующими условиями для a, b, c, и dи формулами для корней
(-b+КОРЕНЬ(D))/(2*a) и (-b-КОРЕНЬ(D))/(2*a).
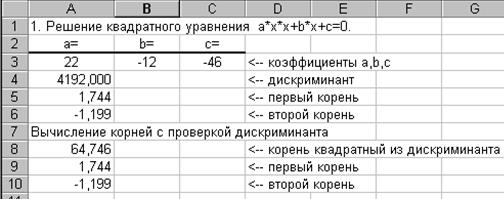 |
Вид электронной таблицы может иметь следующий вид.
Задание 2. Дана таблица с итогами экзаменационной сессии.
Итоги экзаменационной сессии
| № п/п | Ф. И.О. | Математика | Эконом. Теория | Информатика |
| 1. | Макаров С.П. | |||
| 2. | ... | ... | ||
| 3. |
Составить электронную таблицу, определяющую стипендию по следующему правилу:
По рассчитанному среднему баллу за экзаменационную сессию (s) вычисляется повышающий коэффициент (k), на который затем умножается минимальная стипендия (m).
Повышающий коэффициент вычисляется по правилу:
если 4 £ s < 8, то k=1.5,
если 8 £ s < 10, то k=1.8,
если s= 10, то k=2.0
Если же s<4 или s>10, то стипендия не назначается и поэтому нужно в этом случае коэффициент k вычислять специальным образом, например, присвоить k текст «Неправильные данные»
Выполнение.
1. Составить исходную таблицу:
Итоги экзаменационной сессии
| № п/п | Ф. И.О. | Математика | Эконом. Теория | Информатика |
| 1. | Макаров С.П. | |||
| 2. | ... | ... | ||
| 3. | ||||
| … | ||||
| Средний балл |
2. Составить электронную таблицу для выплаты стипендий.
| № п/п | Ф.И.О. | Средний балл | Коэффициент | Стипендия |
| 1. | Макаров С.П. | |||
| ... | ... | |||
· Построить таблицу по образцу
· Графу Ф.И.О. скопировать с исходной таблицы.
· Графы средний балл и стипендия рассчитать по соответствующим формулам с использованием логических функций ЕСЛИ, И, ИЛИ, НЕ.
Задание 3.
По результатам сдачи сессии группой студентов (таблица Итоги экзаменационной сессии), определить
- количество сдавших сессию на "отлично" (9 и 10 баллов);
- на "хорошо" и "отлично" (6-10 баллов);
- количество неуспевающих (имеющих 2 балла);
- самый "сложный" предмет;
- фамилию студента, с наивысшим средним баллом.
Задание 4.
Пусть в ячейках A1,A2,A3 записаны три числа, задающих длины сторон треугольника.
Написать формулу:
- определения типа треугольника (равносторонний, равнобедренный, разносторонний),
- определения типа треугольника (прямоугольный, остроугольный, тупоугольный),
- вычисления площади треугольника, если он существует. В противном случае в ячейку В6 вывести слово "нет".
Дата: 2016-10-02, просмотров: 379.