Присоединение частицы «не» к высказыванию называется операцией логического отрицанияилиинверсией.
Инверсия делает истинное высказывание ложным и наоборот.
Операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать Ā. Образуем высказывание С , являющееся логическим отрицанием А:С=Ā
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического отрицания:
| А | Ā |
| 0 | 1 |
| 1 | 0 |
В рассмотренном нами выше примере А = 1, т.е. полученное в результате логического отрицания высказывание «Не два умножить на два равно четырем» ложно.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут символы, обозначающие высказывания и их отрицания, соединенные знаками логических операций. Правила преобразования логических выражений, аналогичны правилам алгебры.
При преобразовании логических выражений определено следующее старшинство логических операций: инверсия, конъюнкция, дизъюнкция (для изменения указанного порядка могут использоваться скобки).
Высказывания, у которых таблицы истинности совпадают, называютсяравносильными.Для обозначения равносильных высказываний используется знак «=».
Пусть имеются простые высказывания А,В. Докажем, что сложное
высказывание 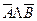 равносильно сложному высказыванию
равносильно сложному высказыванию  . Построим сначала таблицу истинности для логических выражений
. Построим сначала таблицу истинности для логических выражений 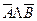 и
и  :
:
| А | В | 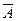
| 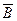
| 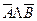
|
| А | В | 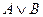
| 
|
| l | |||
| l |
Таблицы истинности совпадают, следовательно, логические выражения равносильны: 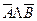 =
= 
Операция логического следования (импликации)
Логическое следование (импликации) образуется соединением двух высказываний в одно с помощью оборота речи «если…., то….»
Логическая операция импликации «если А, то В», обозначается А®В.
Истинность такого высказывания задается специальной таблицей, таблицей истинности:
| А | В | А®В |
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Логическое равенство (эквивалентность).
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда».
Логическая операция эквивалентность «А тогда и только тогда, когда В» обозначается А~В.
Истинность такого высказывания задается специальной таблицей, таблицей истинности:
| А | В | А~В |
Составное высказывание, образованное с помощью логической операции эквивалентность истинно тогда и только тогда, когда оба высказывания либо истины, либо ложны.
Законы логики
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
| Закон | Выражение |
| Закон тождества | А=А |
| Закон непротиворечия | 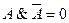
|
| Закон исключения третьего | 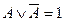
|
| Закон двойного отрицания | 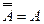
|
| Закон де Моргана | 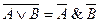
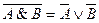
|
| Закон коммутативности | А&B=B&A
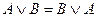
|
| Закон ассоциативности | 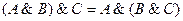
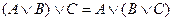
|
| Закон дистрибутивности | 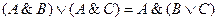
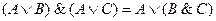
|
Задание 1. По заданному преподавателем варианту для логического выражения построить таблицу истинности и схему логического устройства.
| 1. (Ā& B) V C | 11. (Ā V B)& C | 21. Ā &(B V C) |
| 2. Ā V (B& C) | 12. (A& 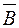 ) V C ) V C
| 22. A&( 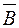 V C) V C)
|
3. (A V 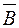 )&C )&C
| 13. A V ( 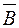 &C) &C)
| 23. (A& B) V 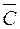
|
4. A& (B V 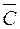 ) )
| 14. (A V B)& 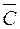
| 24. A V( B& 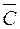 ) )
|
5. (Ā& 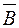 ) V C ) V C
| 15. Ā&( 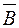 V C) V C)
| 25. (Ā V 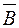 ) &C ) &C
|
6. Ā V ( 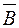 & C) & C)
| 16. (Ā &B) V 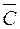
| 26. Ā &(B V 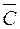 ) )
|
7. (Ā V B)& 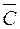
| 17. Ā V (B& 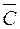 ) )
| 27. (A & 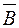 ) V ) V 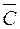
|
8. A &( 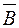 V V 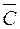 ) )
| 18. (A V 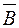 )& )& 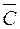
| 28. A V ( 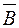 & & 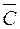 ) )
|
| 9. (Ā V B) V C | 19. Ā &(B& C) | 29. (A V 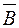 ) V C ) V C
|
10.A&( 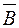 & C) & C)
| 20. (A V B) V 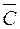
| 30. A&(B& 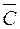 ) )
|
Задание 2. Определите, равносильны ли логические выражения задания 1 и 2
| Варианты | Соответствующие варианты задания 1 |
( 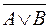 )& )& 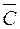
| 1-3 |
( 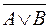 )&C )&C
| 4-6 |
( 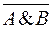 )& )& 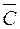
| 7-9 |
( 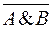 )&C )&C
| 10-12 |
А V ( 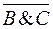 ) )
| 13-15 |
Ā V ( 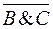 ) )
| 16-18 |
A& ( 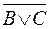 ) )
| 19-21 |
Ā & ( 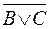 ) )
| 22-24 |
(Ā V B)& 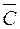
| 25-27 |
Ā &( 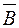 V C) V C)
| 28-30 |
Задание 3.
1. Доказать или опровергнуть с помощью построенных таблиц истинности равносильность следующих логических выражений:
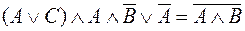 V
V 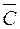
2. Найдите X, если:
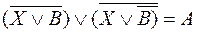
3. Найдите X, если
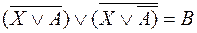
4. Записать составное высказывание «(3*4=12 и5*3=9) или (6*7=36 и 5*5≠45)» в форме логического выражения. Определить истинности или ложность получившегося выражения.
5. Упростить логическую функцию и построить таблицу истинности.
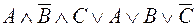
6. Доказать или опровергнуть с помощью построенных таблиц истинности равносильность следующих логических выражений:
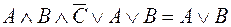 V
V 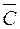
7. Записать составное высказывание «(3*3=12 и 3*3=9) или (6*6=36 и 5*5=45)» в форме логического выражения. Определить истинности или ложность получившегося выражения.
8. Доказать, что логическое выражение является тождественно-истинным.
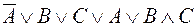
9. Доказать или опровергнуть с помощью построенных таблиц истинности равносильность следующих логических выражений:
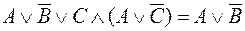 V
V 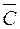
10. Упростить логическую функцию и построить таблицу истинности.
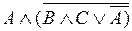
12. Решить логическую задачу:
Аня, Катя и Оля нашли в земле кувшин. Каждая из них высказала свое предположение. Оля: «Это греческий кувшин, изготовленный в V веке». Аня: «Это римский кувшин, изготовленный в III веке». Оля: «Это не греческий кувшин, изготовленный в VII веке». Учитель сказал, что каждая из них права только в одном из своих суждений. Где и когда был изготовлен кувшин?
13. Записать составное высказывание «(3*3=12 и 3*3=9) или (6*6=36 и 5*5≠45)» в форме логического выражения. Определить истинности или ложность получившегося выражения.
14. Упростить логическую функцию и построить таблицу истинности.
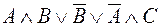
15. Упростить логическую функцию и построить таблицу истинности.
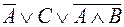
Контрольные вопросы
- Чем заменяются высказывания в алгебре высказываний?
- Построить таблицу истинности операции логического умножения (конъюнкции).
- Построить таблицу истинности операции логического сложения (дизъюнкции).
- Построить таблицу истинности операции логического отрицания (инверсия).
- При каком условии логические выражения равносильны?
- Какой сигнал будет на выходе логического элемента «И», если на входе будут поданы сигналы А=0, В=1?
- Какой сигнал будет на выходе логического элемента «ИЛИ», если на входе будут поданы сигналы А=0, В=1?
- Какой сигнал будет на выходе логического элемента «НЕ», если на вход будет подан сигнал А=0?
Лабораторная работа №3
Тема: «Ввод, редактирование и форматирование текстового документа в MS Word.»
Цель: Приобретение практических навыков форматирования и редактирования текстового документа в программе «Microsoft Word»
ПОРЯДОК ВЫПОЛНЕНИЯ 1 ЧАСТИ
1. 1-й абзац - заголовок отформатировать шрифтомTimes New Roman, кеглем 16, жирным, выровнять по центру.
2. Пустой абзац (2).
3. Отформатировать следующие абзацы (3 и 4) шрифтомArial, кеглем14, жирным, наклонным, каждый с красной строки, выровнен по ширине.
4. Текст 5-го абзаца (Буддийская мудрость) расположитьс нестандартной позиции табуляции, равной 7см.
5. Отформатировать следующий 6 абзац шрифтомTimes New Roman, кеглем16, подчеркнутым.
6. Текст 7-го абзаца (Саади) расположитьс нестандартной позиции табуляции,равной13см.
7. В 8-й абзац - вставить рисунок(м.Вставка, п.Рисунок, из файла, папка С:\Microsoft Office\Clipart).
8. 2 пустых абзаца (9,10).
9. Абзац 11 отформатироватьнаклонным шрифтом, кеглем 12.
Дата: 2016-10-02, просмотров: 464.