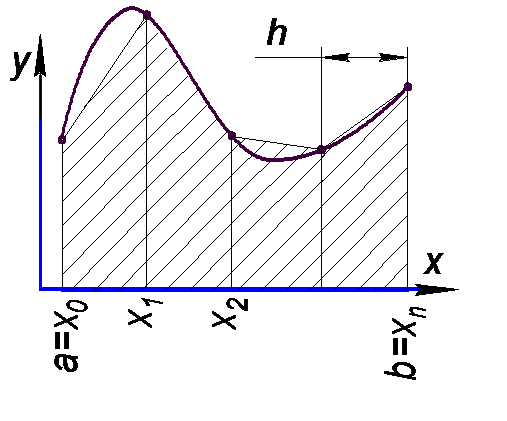
На каждом частичном интервале [x_i , x_i+1 ] заменяют аппроксимирующую функцию f(x) полиномом Лагранжа первой степени, т.е. применяют линейную интерполяцию. График функции в этом случае представляет ломаную линию, соединяющую точки (x_i, y_i ) (Рис.4). В этом случае площадь всей фигуры складывается из площадей элементарных прямоугольных трапеций, равных s_i=h(y_i-1+y_i)/2 (i=1,2,…,n) . Сумма этих площадей и представляет формулу трапеций

.

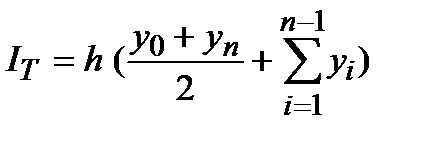Вопрос 15.

Численное интегрирование. Метод Симпсона.

Отрезок интегрирования [a , b] разбивают на четное количество n=2m равных интервалов с шагом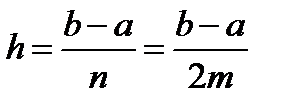

На каждых двух соседних интервалах [x_i-1 , x_i ] и [x_i , x_i+1 ] (i=1,2,…,n-1) , начиная с первого, заменяют функцию полиномом Лагранжа или Ньютона второй степени, т.е. параболой, проходящей через три точки с координатами

(x_i-1, y_i-1 ) , (x_i, y_i ) , (x_i+1, y_i+1 ) и с осью симметрии, параллельной оси ординат (Рис.5).

Площадь каждой пары интервалов равна s_i=(y_i-1+4y_i+y_i+1)×h/2 . Сумма этих площадей и представляет формулу Симпсона

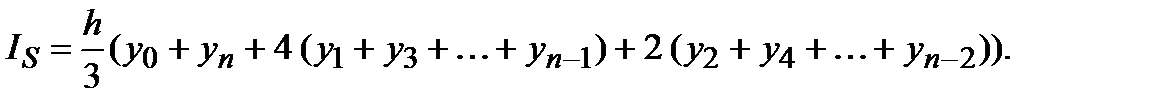
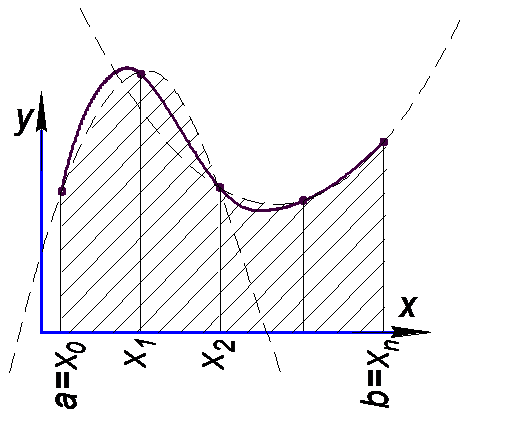
Рис.5. Метод Симпсона

Вопрос 16.Численные методы решения задачи Коши для ОДУ первого порядка. Метод Эйлера.

Метод Эйлера

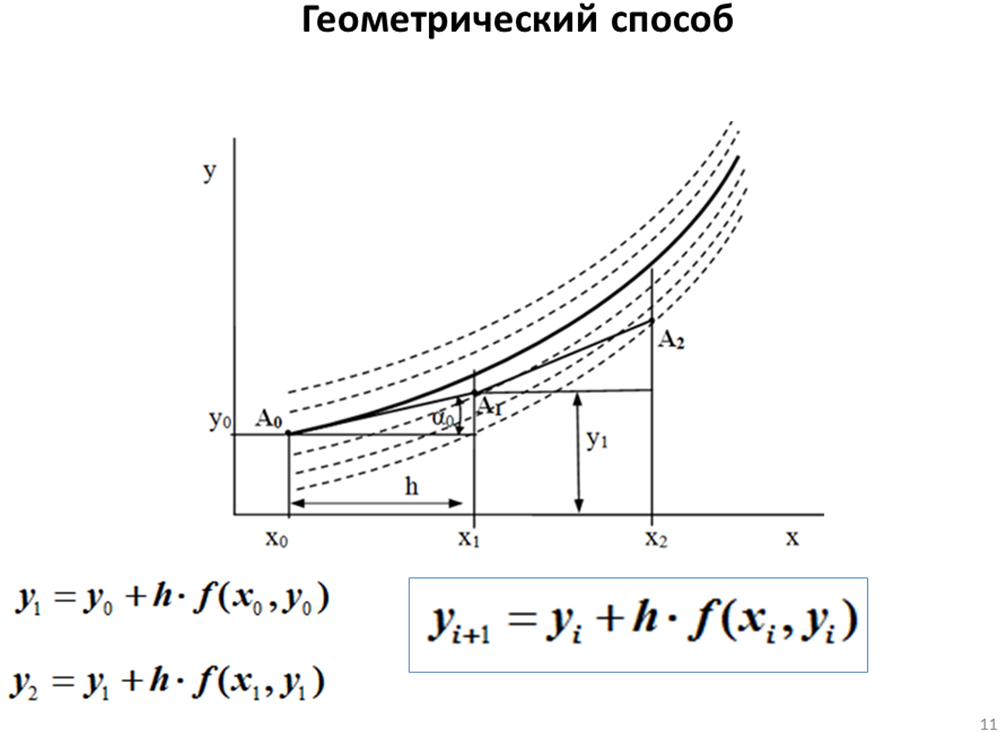
Семейство интегральных кривых (сплошная и пунктирные линии) представляет общее решение дифференциального уравнения.

Точное решение (сплошная линия) в соответствии с начальными условиями проходит через точку А₀ с координатами (x₀,y₀). Заменим точное решение y =j(x) касательной к интегральной кривой в точке А₀ при x=x₀.

При x=x₁ получим точку А₁ с ординатой y₁=y₀+h×tga₀. Получим y₁=y₀+h×f(x₀,y₀), где f(x₀, y₀) - функция, характеризующая наклон касательной в точке А₀. Таким образом, приращение функции заменяем ее дифференциалом. Выполнив аналогичную процедуру в точке А₁, найдем ординату точки А₂ : y₂=y₁+h×f(x₁, y₁).

В общем случае дляi-ой точки можно записать

y_i+1=y_i+h× f(x_i ,y_i ).

Исходной точкой для каждого прямолинейного отрезка является конечная точка предыдущего. Наклон каждого отрезка ломаной определяется значением производной y’(x_i)=f(x_i,y_i).

Вопрос 17.

Первый модифицированный метод Эйлера

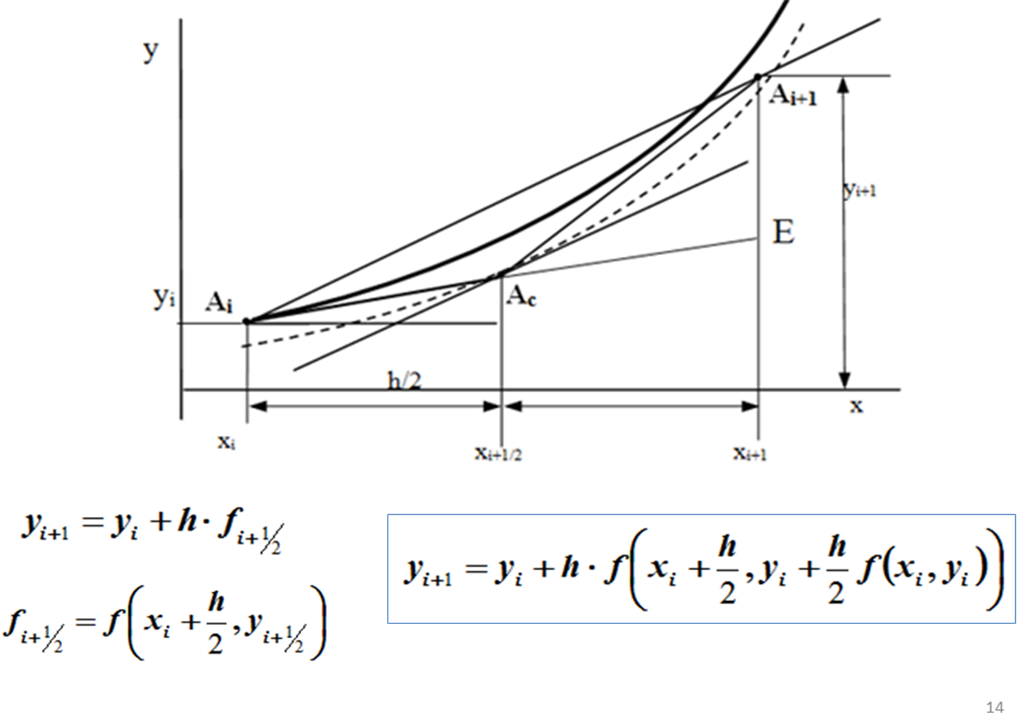
Сначала на каждом i -ом шаге, как и в методе Эйлера, используя наклон касательной в точке A_i (х= x_i), вычисляют промежуточное значение y_i+1/2 , но не на всей длине шага h , а на его половине в средней точке A_c (х=x_i+1/2) каждого интервала [x_i , x_i+1]:

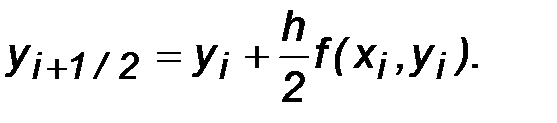
Затем находят направление касательной f_i+1/2 в середине интервала в точке A_c (х=x_i+1/2=x_i+h/2) :

Это направление и принимают за окончательное при вычислении ординаты точки A_i+1 на всем интервале h от точки A_i: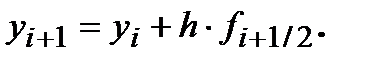

Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки A_i+1:

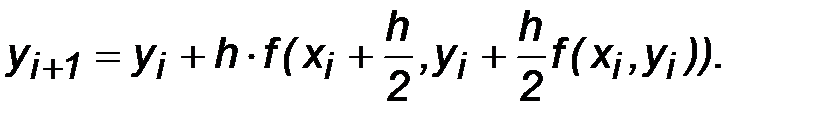
Вопрос 18. Второй модифицированный метод Эйлера

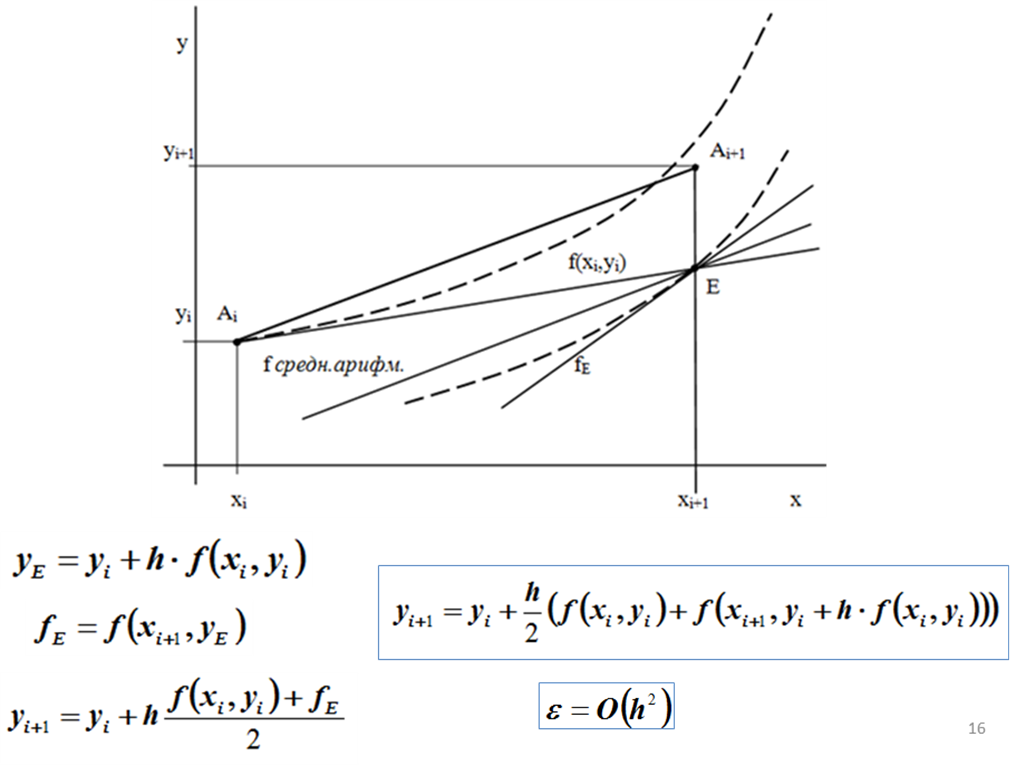
Сначала определяют значение ординаты y_E в точке E как и в методе Эйлера (Рис.4.): y_E=y_i+h×f(x_i, y_i).

В точке E вычисляют направление проходящей через нее интегральной кривой f_E=f(x_i+1,y_E).

В качестве окончательного значения направления кривой на всем отрезке h принимают среднее арифметическое значение от направлений f(x_i , y_i) и f_E , т.е. ординату точки A_i+1 вычисляют по формуле

.

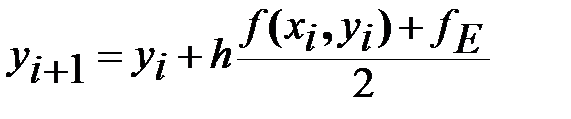Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки A_i+1:

.

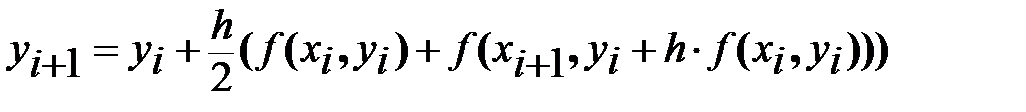Локальная погрешность обоих модифицированных методов О(h³) , глобальная - О(h²) .

Все методы Эйлера являются явными и одношаговыми , поскольку для вычисления последующего приближения необходимо знать только значение функции f(x,y) на предыдущем шаге.

Вопрос 19.Метод Рунге-Кутты.

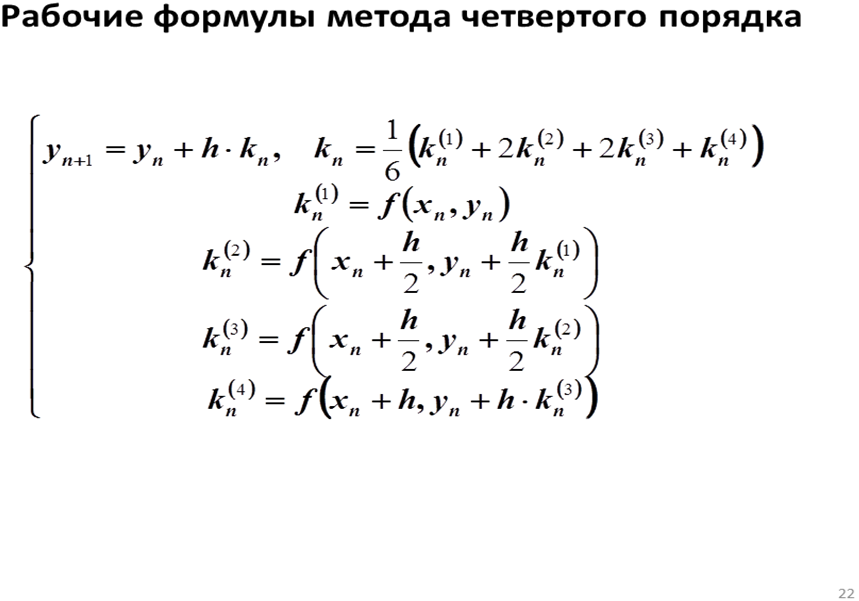
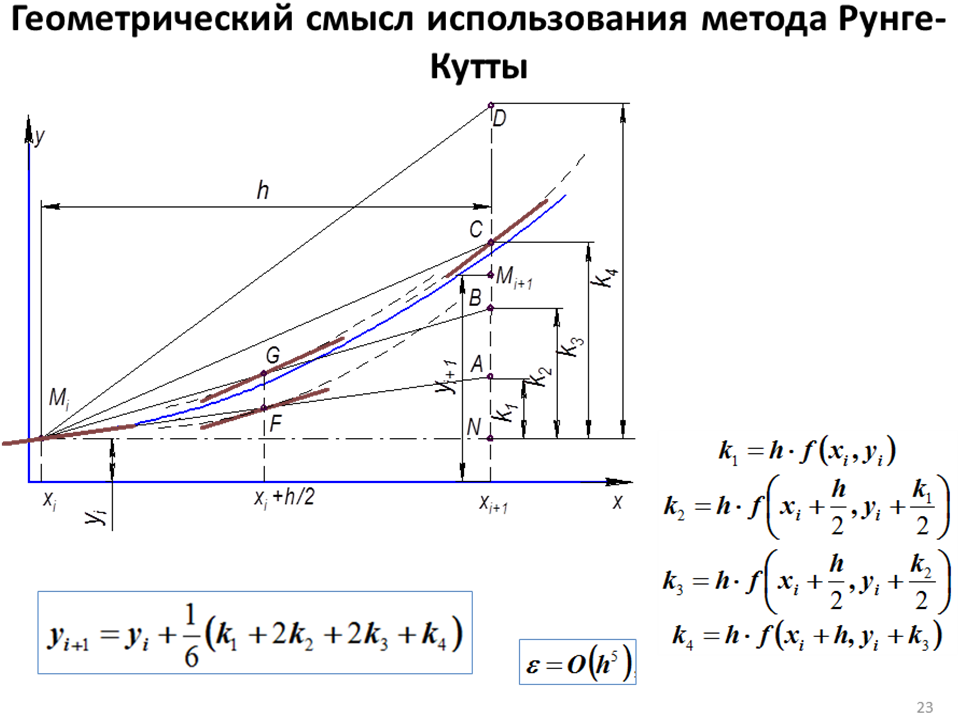
1. Из точки M_i с координатами (x_i,y_i) строят касательную в направлении, определяемым углом α₁ , для которого tg α₁=f(x_i,y_i) и находят точку A.

Расстояние NA будет k₁= hf(x_i,y_i).

2. При x=x_i+h/2 в точке F вычисляют наклон второй касательной с углом α₂ (касательная показана утолщенным отрезком) tg α₂=f(x_i+h/2,y_i+k₁/2). С этим наклоном проводят прямую из точки M_i и получают точку B .

При этом приращение будет NBk₂=hf(x_i+h/2,y_i+k₁/2).

3. Также при x=x_i+h/2, но уже в точке G пересечения прямой M_i B с одной из кривых семейства, вычисляют ее наклон (касательная показана утолщенным отрезком) как tgα₃=f(x_i+h/2 , y_i+k₂/2). С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение NC, равное k₃=hf(x_i+h/2,y_i+k₂/2).

Второй и третий этапы представляют не что иное, как модифицированные методы Эйлера.

4. При x=x_i+1 в точке С пересечения прямой M_iC с одной из кривых семейства вычисляют ее наклон (касательная также показана утолщенным отрезком) как tgα₄=f(x_i+h , y_i+k₃). С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение ND, равное k₄=hf(x_i+h,y_i+k₃).

5. Окончательно приращение ординаты точки M_i+1 вычисляют как средневзвешенную величину приращений k₁, k₂, k₃, k₄ , с весовыми коэффициентами 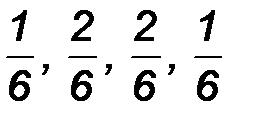соответственно

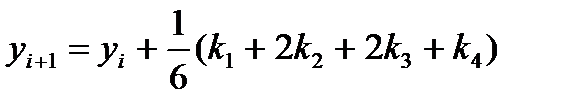
Где k₁= hf(x_i,y_i).

k₂=hf(x_i+h/2,y_i+k₁/2).

k₃=hf(x_i+h/2,y_i+k₂/2).

k₄=hf(x_i+h,y_i+k₃).

Вопрос 20.Численные методы решения задачи Коши для системы ОДУ первого порядка.

Определение :

Система дифференциальных уравнений называется нормальной , если все уравнения системы разрешены относительно старшей производной.

Рассмотрим систему ДУ вида :

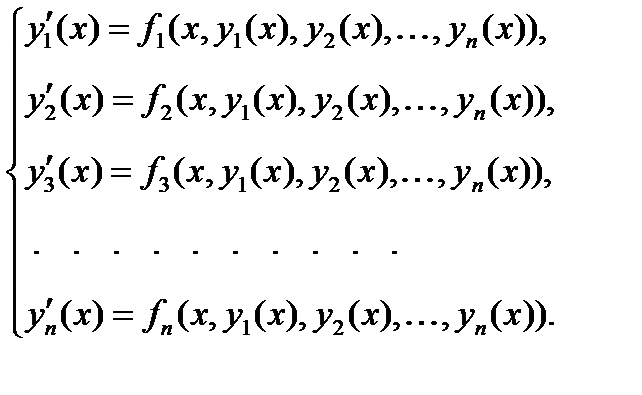
- искомые функции на промежутке [x₀,X]

Заданы начальные условия :

Введем понятие вектор-функции :

, ,

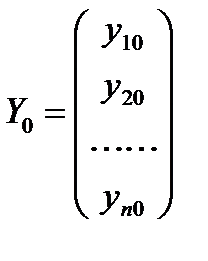
Тогда имеем :

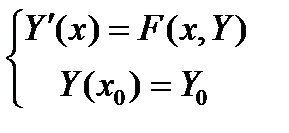
Вопрос 21. Решение ОДУ высших порядков.