Здесь необходимо требование , что первая и вторая производные непрерывны и сохраняют знаки на выбранном промежутке.

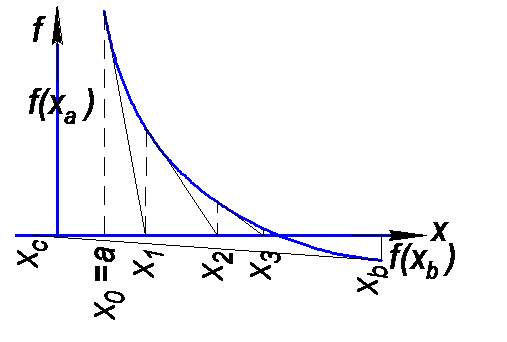
Формула метода может быть получена из предположения, что поправка h мала и можно использовать формулу Тейлора

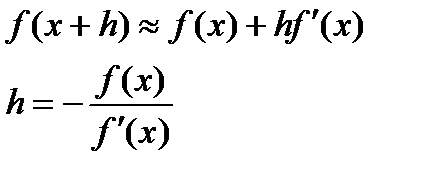
Алгоритм метода:

1. За начальное приближение x₀ принимают граничную точку, в которой знак функции совпадает со знаком второй производной, т.е. f(x₀)×f’’(x₀)>0;

2. Каждое следующее значение абсциссы x_i+1 вычисляют как точку пересечения касательной, проведенной в текущей точкой кривой x_i , с осью абсцисс по формуле: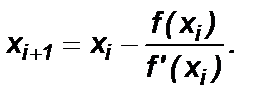

3. Если |x_i+1 – x_i | > e , то цикл повторяют, начиная с п.2, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.

Достоинства метода: простота алгоритма, высокая скорость сходимости. Недостатки: необходимость отыскания первой производной в аналитической форме, ненадежность отыскания корня в указанном диапазоне. На рис.3 показано, что в случае проведения касательной в точке b , она может пересечься с осью x в точке c, лежащей за пределами выбранного интервала [a,b], и корень может быть найден совсем в другом интервале.

Вопрос 9.Численные методы решения алгебраических и трансцендентных уравнений. Метод итераций.

Алгоритм метода:

1. Исходное уравнение f(x)=0 преобразуют к виду: x=j(x)

2. Левая часть этого уравнения представляет уравнение прямой линии, проходящей через начало координат под углом в 45° к оси x. Абсцисса пересечения этой прямой с функцией j (x)и представляет корень уравнения f(x)=0

3. Задают начальное приближение x₀ и вычисляют значение функции j (x₀) Из следует, что его можно принять за первое приближение x₁ : x₁=j (x₀).

4. Вычислив функ j (x₁) , принимают это значение за 2е приближение x₂=j (x₁) и так далее. В общем случае для (i+1)-й итерац можно записать:x_i+1=j (x_i ) .

5. Итерации повторяют, пока выполняется условие |x_i+1 – x_i | > e .

Геометрическая интерпретация метода показана на рис.4, причем на рис.4а) и 4б) процесс сходится к корню уравнения f(x)=0, а на рис.4в) и 4г) – расходится, хотя начальное приближение x₀ и выбрано для них ближе к корню.

Из рис.4а) можно заметить, что угол наклона касательной к любой точке кривой y=j (x) не превышает 45° к оси x , т.е. j’(x)<1 . Из рис.4б) следует, что для этого случая j’(x)>-1.

На рис.4в) и 4г) это условие не соблюдается и итерационный процесс на них расходится от корня уравнения.

Отсюда следует, что для обеспечения сходимости итерационного процесса должно соблюдаться условие:

|j’(x)|<1

Вопрос 10.Решение систем линейных алгебраических уравнений. Метод Гаусса.

Рассмотрим СЛАУ:

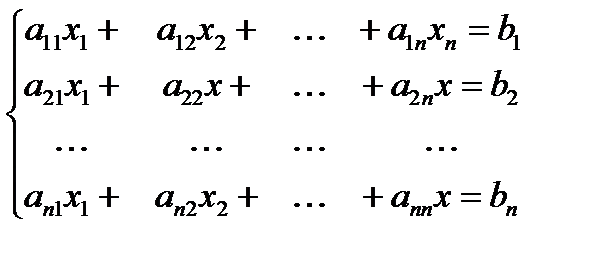
или в матричном виде ,

где А –квадратная матрица размерности n x n .

x,b – n- мерные векторы , i=1,2,…,n

Будем полагать , что матрица А невырожденная , т.е. детерминант úАç¹0 и, следовательно, решение СЛАУ существует и оно единственное.

Основная идея метода состоит в том, чтобы исходную СЛАУ A× x=b

методом исключения свести к системе вида A’× x = b’, где A’ – треуг. матр.

Рассмотрим более подробно процесс преобразования исходной матрицы A к треугольной A’. Предполагая, что a₁₁ ¹ 0 , разделим первое уравнение СЛАУ на коэффициент a₁₁:

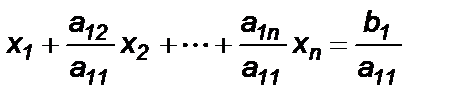
Вычтем полученное уравнение из всех остальных уравнений , умножая его на соответствующий коэффициент a_i1 . В результате первое неизвестное x₁ окажется исключенным из всех уравнений, кроме первого, и СЛАУ примет вид:

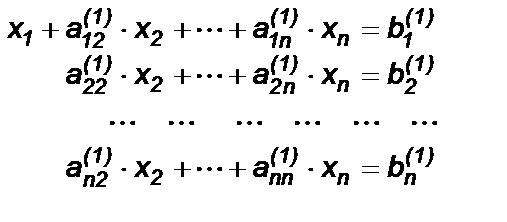
где

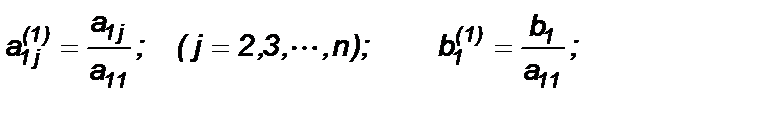
Далее, предполагая, что a₂₂ ¹ 0, делим второе уравнение преобразованной системы на коэффициент . Затем также умножаем его на соответствующие коэффициенты a_i2 и вычитаем из всех оставшихся уравнений преобразованной системы , при этом из них будут исключены неизвестные x₂ , начиная с третьего уравнения. Продолжая этот процесс исключения неизвестных, вместо второй системы получим эквивалентную систему :

В общем случае формулы имеют вид :

а) для коэффициентов в самом верхнем уравнении на k- ом шаге исключения

б) для остальных коэффициентов

Процесс сведения СЛАУ к системе с треугольной матрицей называется прямым ходом метода Гаусса. Выполнение указанных преобразований возможно, если получающиеся при расчете коэффициенты 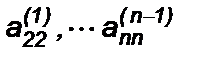отличны от нуля. В противном случае нужно производить перестановку уравнений, т.к. среди коэффициентов 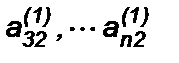обязательно найдется хотя бы один, отличный от нуля, - иначе матрица A была бы вырожденной.

В результате прямого хода СЛАУ приобретает вид:

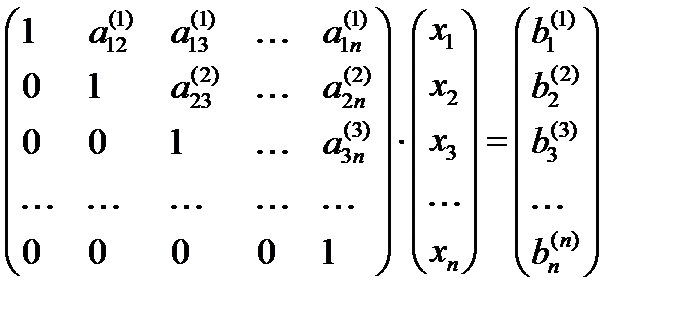
Из последнего уравнения находится x_n , затем из предпоследнего x_n-1 и т.д.

Этот этап решения называют обратным ходом метода Гаусса.

В результате обратного хода

Общ. числ арифм. операций S, по формуле S = 2/3×n×(n+1)×(n+2) + n×(n-1),

где n - кол-во неизвестных. При больших n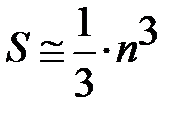

Вопрос 11.