Интерполяция – способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
В различных областях науки и техники часто возникает задача приближенной замены некоторой зависимости f(x) другой функцией j(x) таким образом, чтобы отклонение функции j(x) от f(x) на заданном отрезке [a , b] было наименьшим. Функция j(x) называется аппроксимирующей, а сама процедура замены – аппроксимацией. Если приближение строится на дискретном множестве точек xi, то такая аппроксимация называется точечной. Одним из основных типов точечной аппроксимации является интерполирование.
Задача интерполирования: для функции y=f(x) построить функцию, принимающую в заданных точках xi, называемых узлами интерполирования, те же значения yi, что и функция f(x), т.е. j(x)=yi , (i=0,1,…,n).
Функция y=f(x) может быть задана в виде координат точек xi и yi, полученных например экспериментальным путем.
Пусть на отрезке [a , b] в неравноотстоящих n+1 узлах x0, x1, . . . , xn известны значения функции y0=f(x0) , y1=f(x1) , . . . , yn =f(xn) . Требуется построить многочлен L(x) так, чтобы в узлах x0, x1, . . . , xn его значения совпадали со значениями заданной функции, т.е. L(x0)=y0 , L(x1)=y1 , . . . ,L(xn)=yn .
Будем искать многочлен степени не выше n
L(x)=a0+a1x+a2x2+. . . +anxn , (1)
где a0, a1, . . . , an - постоянные коэффициенты, которые требуется найти.
Подставим вместо x значения x0, x1, . . . , xn, а вместо L(x) их значения y0, y1, . . . , yn. Получим систему уравнений
a0+a1 x0+ a2 x02+¼ + an x0n = y0
a0+a1 x1+ a2 x12+¼ + an x1n = y1 (2)
. . . . . . . . . . . .
a0+a1 xn+ a2 xn2+¼ + an xnn = yn
Решение этой системы позволит определить все коэффициенты a0, a1, . . . , an многочлена (1). Так и поступают, когда требуется многократно использовать многочлен (1). Для разового использования гораздо быстрее и удобнее воспользоваться многочленом в форме Лагранжа, который предложил линейную комбинацию многочленов степени n:
L(x)=y0 l0(x)+ y1 l1(x)+ . . . + yn ln(x) (3)
Потребуем, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением одного i-го, где он должен равняться единице. Этим условиям отвечает многочлен вида
 (4)
(4)
Действительно, при x=x0 l0(x0)=1 . При всех остальных значениях x=x1, x2, . . . , xn числитель выражения (4) обращается в нуль. По аналогии с (4) получим
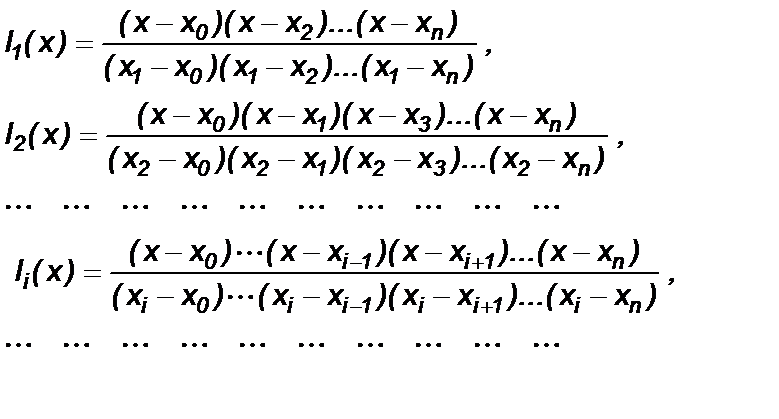 (5)
(5)
Подставляя в (3) выражения (4) и (5), получим

или в более компактной записи
 (6)
(6)
Эта формула называется интерполяционным многочленом Лагранжа. Она позволяет избавиться от необходимости вычисления коэффициентов a0, a1, . . . , an в (1) путем решения системы (2), а использовать только известные значения узлов интерполяции. Непременное условие – отсутствие совпадающих узлов.
Вопрос 5.
Интерполяция дискретных данных. Формула Ньютона.
Если нужно повысить точность аппроксимации за счет увеличения степени полинома, пользоваться формулой Лагранжа неудобно, так как по ней приходится все слагаемые пересчитывать заново. Формула Ньютона позволяет в этом случае лишь добавить недостающие члены. Эта формула использует аппарат конечных разностей.
Для этого используем таблицу:
| x = x0 + i h | f (k) | D f | D2 f | D3 f |
| X0 | f0 | D f0 | D2 f0 | D3 f0 |
| x0 + h | f1 | D f1 | D2 f1 | |
| X0 + 2h | f2 | D f2 | ||
| X0 + 3h | f3 |
Df – конечные разности первого порядка.
Они определяются по формулам:
D f0 = f1 – f0 ; D f1 = f2 – f1 ; D f2 = f3 – f2.
Конечные разности второго порядка D2f рассчитываются по формулам
D2 f0 = Df1 – Df0 = f2 – 2f1 + f0,
D2 f1 = Df2 – Df1 = f3 – 2f2 + f1.
Конечная разность третьего порядка D3f0 рассчитывается по формуле
D3f0 = D2f1 – D2f0 = f3 – 3f2 + 3f1 – f0 .
Будем искать полином по формуле Ньютона в виде:
y (x) = A0 + A1 (x – x0) + A2 (x – x0) (x – x1) + ... + An (x – x0) ... (x – x n–1).
Положим x = x1 , тогда y1 = y0 +A1(x1 – x0), откуда

 .
.
Положим x = x2 , тогда

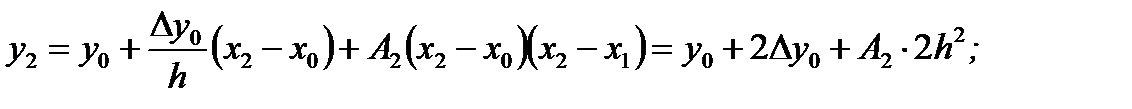

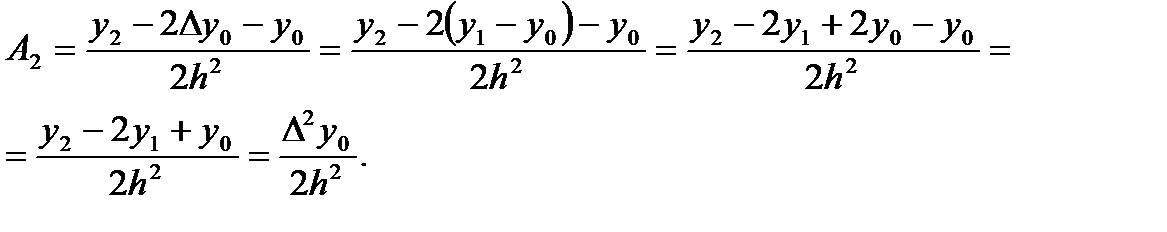
В результате получим полином вида
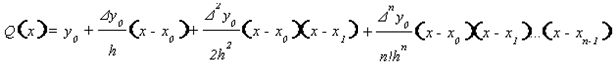
Вопрос 6.
Дата: 2016-10-02, просмотров: 265.