Пусть задана система уравнений в виде, в котором диагональные элементы a_ii ¹ 0 (i =1,2,…n). Выразим x₁ через первое уравнение системы, x₂ - через второе уравнение и т.д. В результате получим эквивалентную систему:

Обозначим 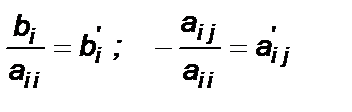, где i = 1,2, …,n ; j = 1,2, … n.

Тогда систему можно записать в матричной форме как X=b’+a’Xили

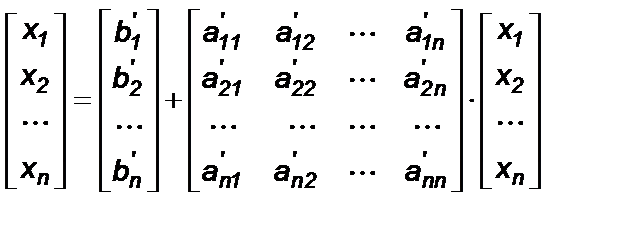
Систему такого вида называют системой, приведенной к нормальному виду. При таком способе приведения все коэффициенты a_ii главной диагонали будут равны нулю.

Зададимся начальным приближением X⁽⁰⁾ , например, таким:

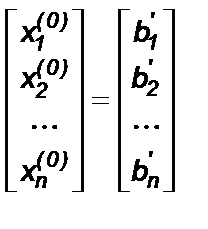- нулевое приближение.

Вычислим значения X⁽¹⁾ первого приближения :

- первое приближение.

Подставим значения X⁽¹⁾ в правую часть уравнения:

- второе приближение,

и т.д., т.е. любое последующее приближение вычисляют по формуле

X^(k+1)=b’+a’X^(k)(k=0,1, … ,n).

Если последовательность приближений X⁽⁰⁾ ,X⁽¹⁾ , …, X^(k) имеет предел 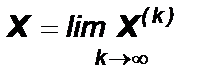, то этот предел и является решением исходной системы. При заданной допустимой погрешности e за критерий окончания итерационного процесса можно принять условие .

Вопрос 12. Приближенное дифференцирование с помощью конечных разностей.

Используем значения y_n-1 = f(x_n-h) и y_n+1 = f(x_n+h) и найдём приближенное значение производной в точке x_n по формуле

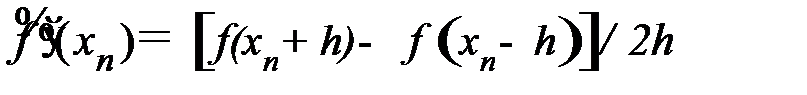
Известно, что в математическом анализе производную определяют как предел выражения(4.1):

f '(x_n) =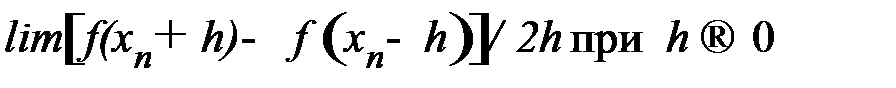

Методическая погрешность

D_мет = h²/3!*(|f'''(x)|)

при h<1 пропорциональна h².

Погрешность реализации D_реал примем равной Df/h. Она растёт с уменьшением h и при этом D_реал®¥ при h®0. Полная погрешность

D_полн = D_мет + D_реал = h²/3!*|f'''(x)| + Df/h

При фиксированных параметрах задачи (точность вычисления значений функции f(x), среднее значение f'''(x)) можно определить координаты точки минимума полной погрешности:

h_оптим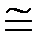

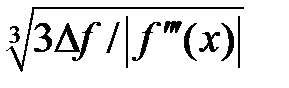
1. Одним из самых простых методов является аппроксимация производной, являющейся пределом отношения приращения функции Dy к приращению аргумента Dx, отношением конечных разностей y¢ » Dy/Dx .

2. Пусть функция задана в табличном виде значениями y = y₀, y₁, . . . , y_n при значениях аргумента x = x₀, x₁, . . . , x_n . Пусть шаг между соседними значениями аргумента Dx=x_i+1 - x_i постоянный и равен h=Dx . В зависимости от способа вычисления конечных разностей получим и разные формулы для вычисления производной в одной и той же точке, например, при x = x₁ .

3. Ведем обозначения индексов для левых конечных разностей - L, правых – R, центральных – C. Тогда для левых разностей будем иметь:

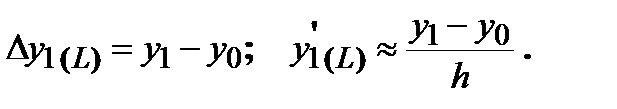
Для правых разностей: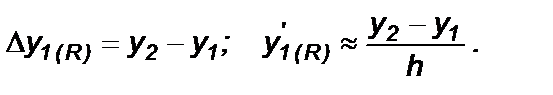

Для центральных разностей: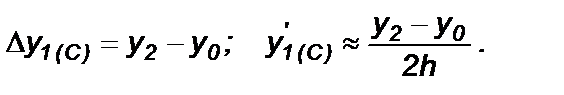

Вопрос 13.Численное интегрирование. Метод прямоугольников.

Потребность в приближенном выч.интег. возникает , когда не существует или неизвестен метод отыскания точного значения или когда этот метод сложный. В случае задания функции в табличной форме приближенные методы являются единственными. Все приближенные методы основаны на следующем положении: рассматривая интеграл как площадь криволинейной трапеции, можно получить его приближенное значение, если вычислить площадь другой трапеции, ограничивающая линия которой по возможности мало отличается от заданной.

Методы прямоугольников

Значение функции является левой точкой частичного интервала

[x_i , x_i+1 ]. Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

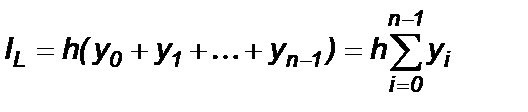. (1)

Ее называют первой формулой прямоугольников или формулой прямоугольников с левыми ординатами.

Значение функции является правой точкой частичного интервала [x_i , x_i+1 ]

Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

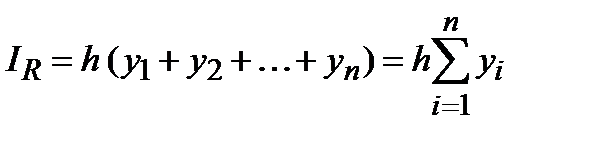. (2)

Ее называют второй формулой прямоугольников или формулой прямоугольников с правыми ординатами.

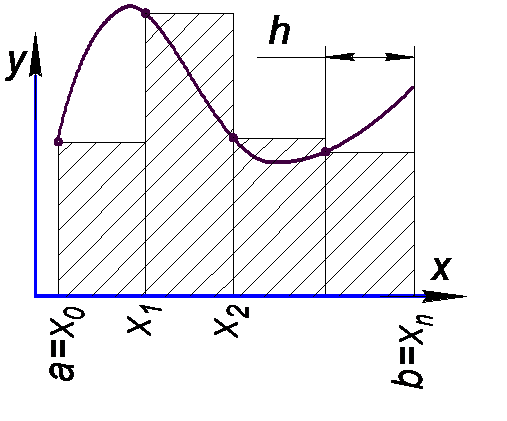
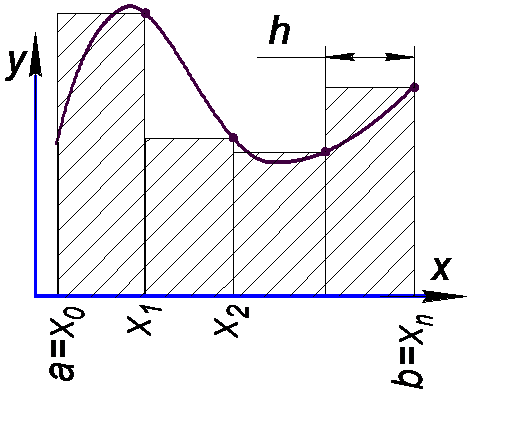
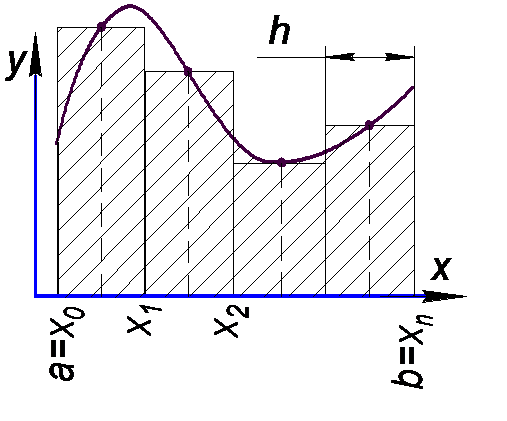
Рис.1. Метод левых ординат	Рис.2. Метод правых ординат	Рис.3. Метод средних

Значение функции является средней точкой частичного интервала

[x_i , x_i+1 ] (Рис.3). Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

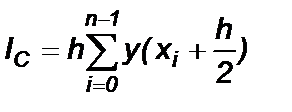. (3)

Вопрос 14.