Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Абсол. и относител. погрешности суммирования и вычитания чисел.

Источники и классификация погрешностей

Источниками возникновения погрешности:

Неточность математического описания (например экспериментальные начальные данные).

Неточность численного метода (ограничения количества арифметических операций вычисления).

Конечная точность машинного счета.

 

Виды погрешностей:

Неустранимая погрешность – неточность задания числовых данных и погрешность математической модели.

Погрешность метода – считается устранимой.

Вычислительная погрешность – или погрешность округлений.

Абсолютная и относительная погрешности. Форма записи данных

Абсолютная.

x – точное значение некоторой величины.

x^*- известное приближение к нему.

D( x^*) - абсолютная погрешность x^* .

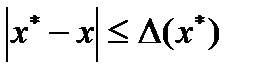
Имеют ту же размерность, что х.

Относительная.

d(x^*) - относительная погрешность.

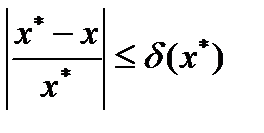
Безразмерна и выражена в долях или процентах.

Вычислительная погрешность

e - абсолютная погрешность.

d - относительная погрешность.

Погрешность суммирования чисел: Имеем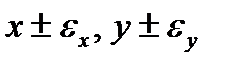

Абсолютная погрешность: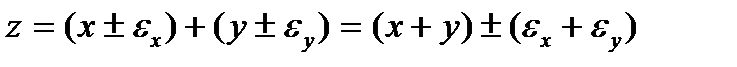

Относительная погрешность:

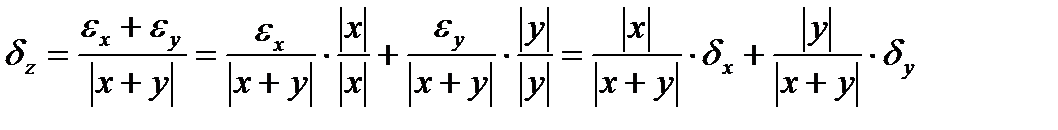
Погрешность вычитания:

Абсолютная погрешность

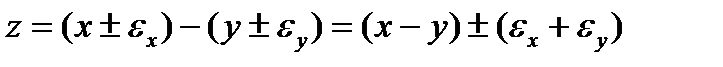
Относительная погрешность

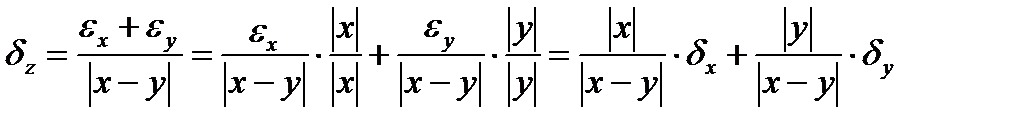
Вопрос 2.

 

Абсолютная и относительная погрешности умножения и деления чисел.

Можно не учитывать

Умножения

Абсолютная погрешность

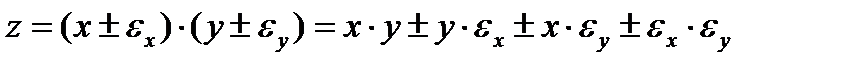
Относительная погрешность

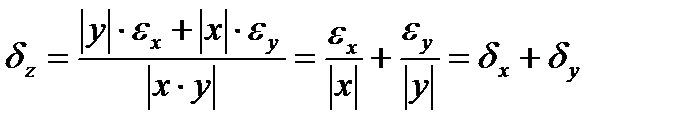
Деления

Абсолютная погрешность

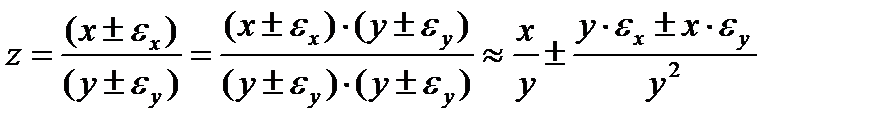
Относительная погрешность

 

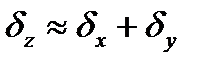
Вопрос 3.

Аппроксимация дискретных данных

Метод наименьших квадратов

Аппроксимация – замена функции другой более удобной (приближенной).

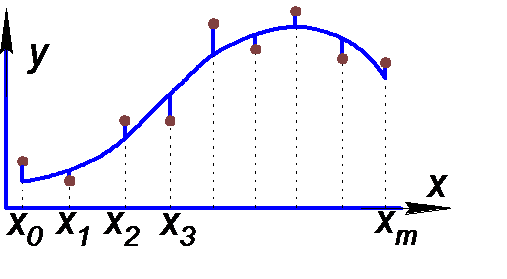
Метод наименьших квадратов применяют, когда необходимо вывести формулу аппроксимирующей кривой, описывающей зависимость, полученную в результате, например, эксперимента. (экспериментальные данные получают с погрешностью).

Кривая не проходит через экспериментальные точки, но учитывает исследуемую закономерность, сглаживая случайные выбросы.

 

В качестве аппроксимирующей функции может использоваться линейная комбинация F(x) любых функций:

 

F(x)= a₀f₀(x)+a₁f₁(x)+ … + a_nf_n(x) ,

f₀(x), f₁(x),…, f_n(x) - набор любых функций (базисные).

a₀ ,a₁ ,… ,a_n - набор коэффициентов.

 

Требуется определить коэффициенты a₀ ,a₁ ,… ,a_n полинома

P (x)=a₀+a₁x+ … +a_nxⁿ

 

таким образом, чтобы сумма S квадратов отклонений полинома P(x) от значений y_i аппроксимируемой функции в заданных точках была бы минимальной, т.е.

 

 

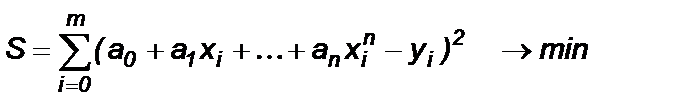
Вопрос 4.

 

Интерполяция дискретных данных. Формула Ньютона.

Если нужно повысить точность аппроксимации за счет увеличения степени полинома, пользоваться формулой Лагранжа неудобно, так как по ней приходится все слагаемые пересчитывать заново. Формула Ньютона позволяет в этом случае лишь добавить недостающие члены. Эта формула использует аппарат конечных разностей.

Для этого используем таблицу:

x = x0 + i h	f (k)	D f	D2 f	D3 f
X0	f0	D f0	D2 f0	D3 f0
x0 + h	f1	D f1	D2 f1
X0 + 2h	f2	D f2
X0 + 3h	f3

 

Df – конечные разности первого порядка.

Они определяются по формулам:

D f₀ = f₁ – f₀ ; D f₁ = f₂ – f₁ ; D f₂ = f₃ – f₂.

Конечные разности второго порядка D²f рассчитываются по формулам

D² f₀ = Df₁ – Df₀ = f₂ – 2f₁ + f₀,

D² f₁ = Df₂ – Df₁ = f₃ – 2f₂ + f₁.

Конечная разность третьего порядка D³f₀ рассчитывается по формуле

D³f₀ = D²f₁ – D²f₀ = f₃ – 3f₂ + 3f₁ – f₀ .

 

Будем искать полином по формуле Ньютона в виде:

y (x) = A₀ + A₁ (x – x₀) + A₂ (x – x₀) (x – x₁) + ... + A_n (x – x₀) ... (x – x _n–1).

Положим x = x₁ , тогда y₁ = y₀ +A₁(x₁ – x₀), откуда

.

Положим x = x₂ , тогда

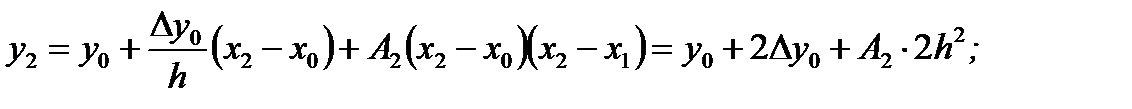
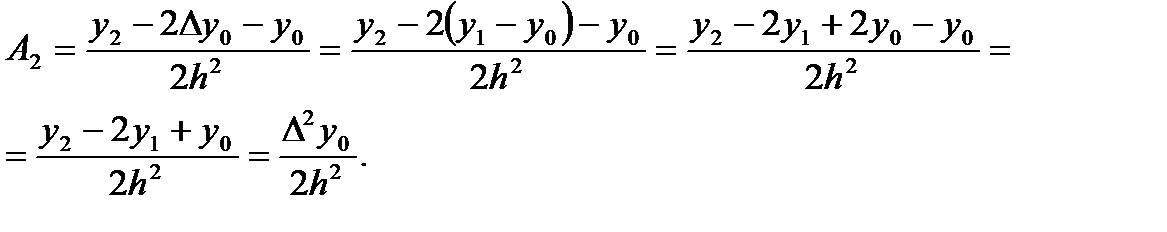
В результате получим полином вида

 

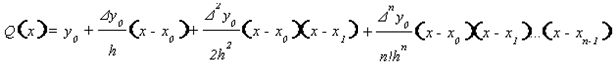
Вопрос 6.

 

Методы прямоугольников

Значение функции является левой точкой частичного интервала

[x_i , x_i+1 ]. Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

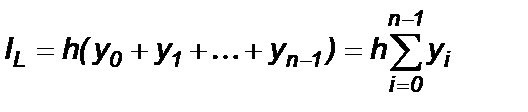. (1)

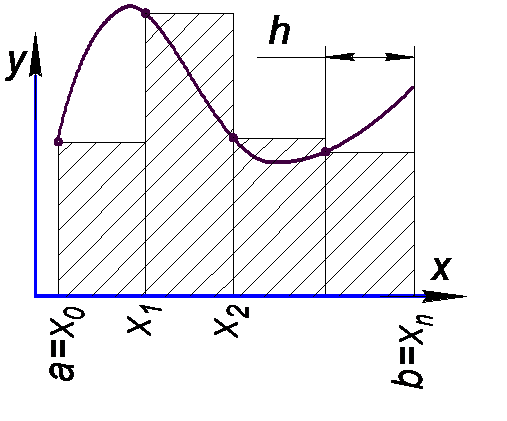
Ее называют первой формулой прямоугольников или формулой прямоугольников с левыми ординатами.

Значение функции является правой точкой частичного интервала [x_i , x_i+1 ]

Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

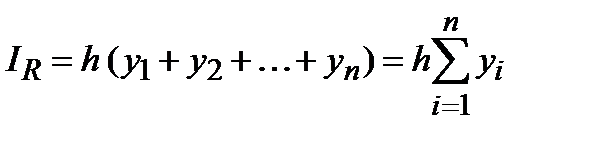. (2)

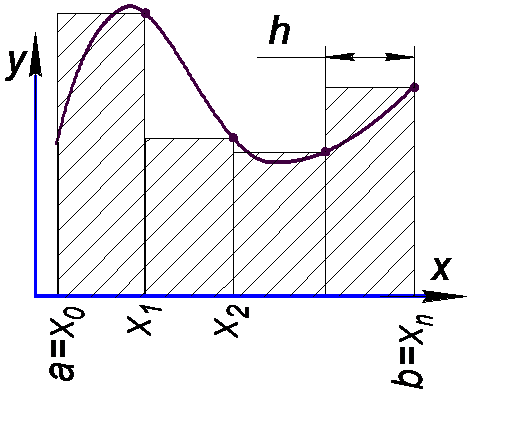
Ее называют второй формулой прямоугольников или формулой прямоугольников с правыми ординатами.

Рис.1. Метод левых ординат	Рис.2. Метод правых ординат	Рис.3. Метод средних

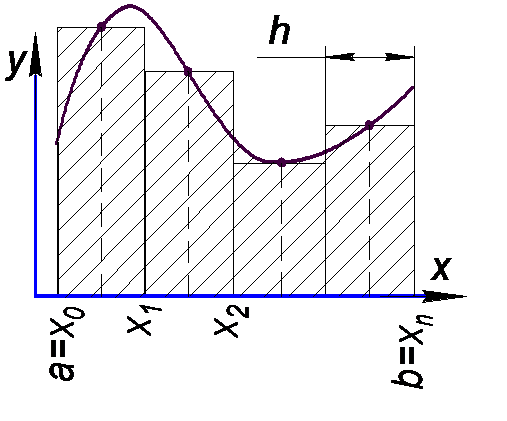
Значение функции является средней точкой частичного интервала

[x_i , x_i+1 ] (Рис.3). Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

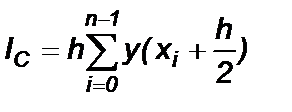. (3)

Вопрос 14.

 

Метод Эйлера

 

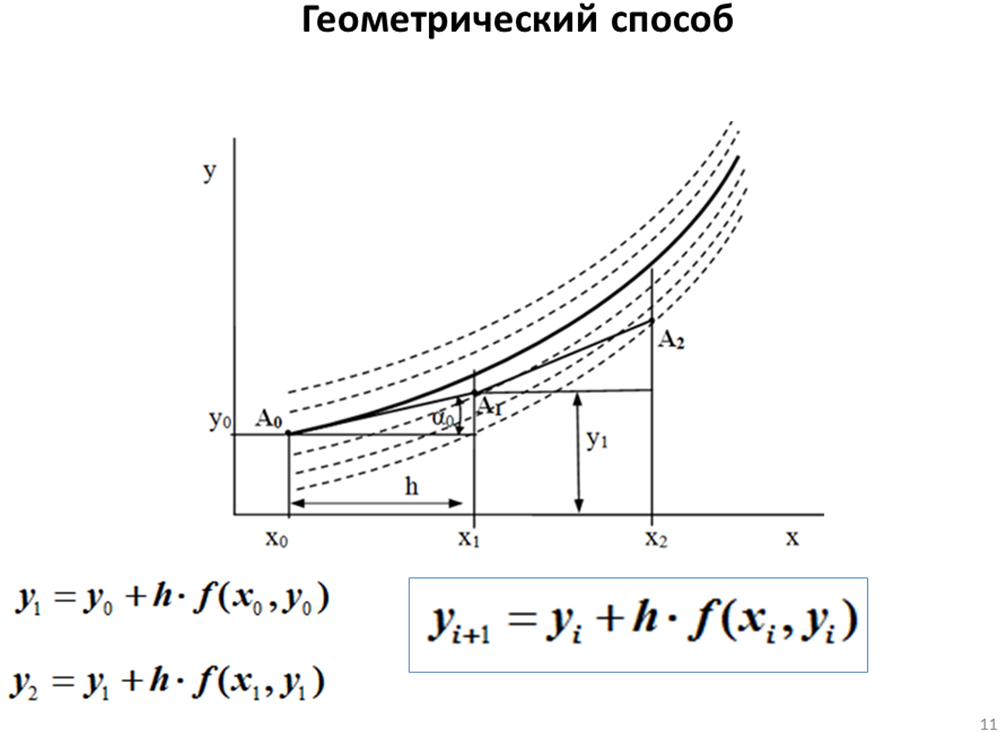
Семейство интегральных кривых (сплошная и пунктирные линии) представляет общее решение дифференциального уравнения.

Точное решение (сплошная линия) в соответствии с начальными условиями проходит через точку А₀ с координатами (x₀,y₀). Заменим точное решение y =j(x) касательной к интегральной кривой в точке А₀ при x=x₀.

При x=x₁ получим точку А₁ с ординатой y₁=y₀+h×tga₀. Получим y₁=y₀+h×f(x₀,y₀), где f(x₀, y₀) - функция, характеризующая наклон касательной в точке А₀. Таким образом, приращение функции заменяем ее дифференциалом. Выполнив аналогичную процедуру в точке А₁, найдем ординату точки А₂ : y₂=y₁+h×f(x₁, y₁).

В общем случае дляi-ой точки можно записать

y_i+1=y_i+h× f(x_i ,y_i ).

Исходной точкой для каждого прямолинейного отрезка является конечная точка предыдущего. Наклон каждого отрезка ломаной определяется значением производной y’(x_i)=f(x_i,y_i).

 

Вопрос 17.

 

Первый модифицированный метод Эйлера

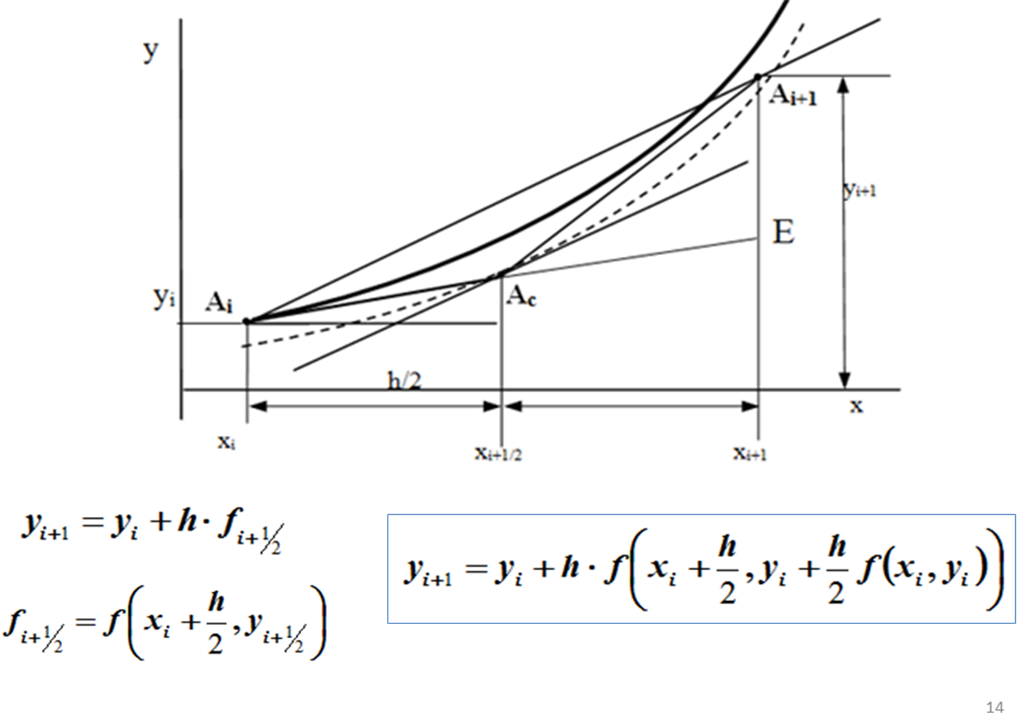
Сначала на каждом i -ом шаге, как и в методе Эйлера, используя наклон касательной в точке A_i (х= x_i), вычисляют промежуточное значение y_i+1/2 , но не на всей длине шага h , а на его половине в средней точке A_c (х=x_i+1/2) каждого интервала [x_i , x_i+1]:

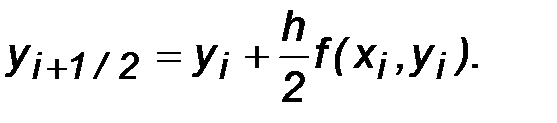
Затем находят направление касательной f_i+1/2 в середине интервала в точке A_c (х=x_i+1/2=x_i+h/2) :

Это направление и принимают за окончательное при вычислении ординаты точки A_i+1 на всем интервале h от точки A_i: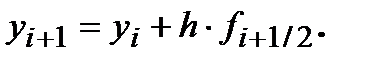

Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки A_i+1:

 

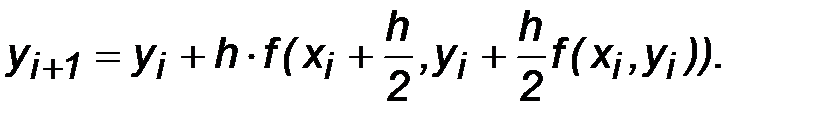
Вопрос 18. Второй модифицированный метод Эйлера

 

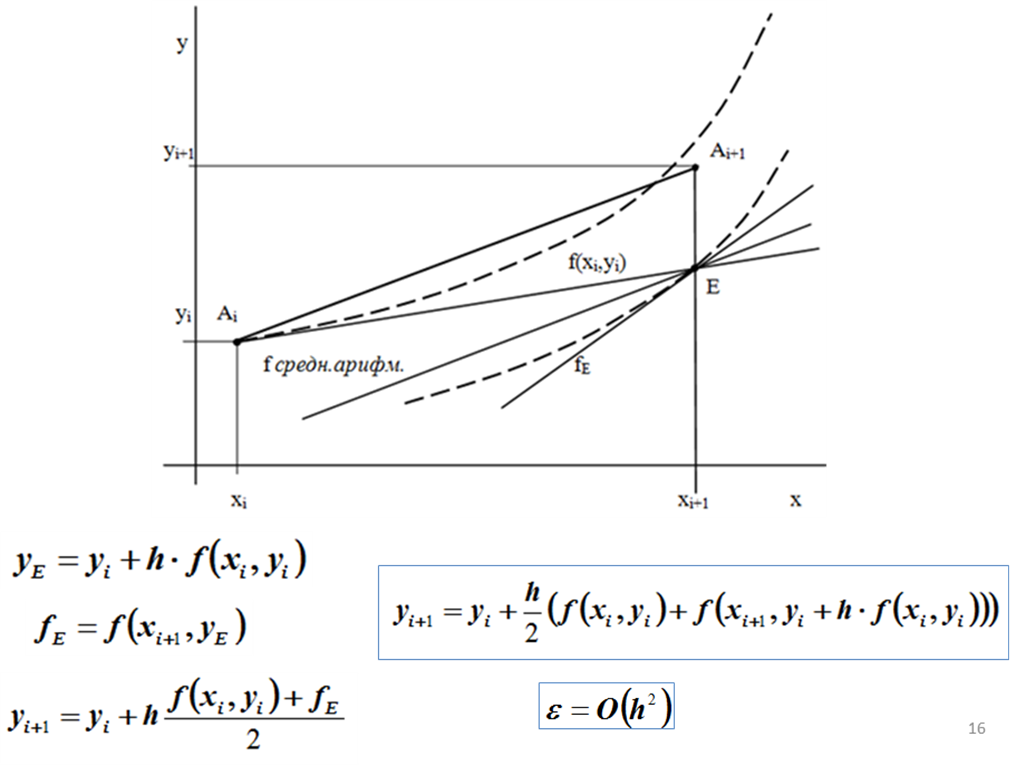
Сначала определяют значение ординаты y_E в точке E как и в методе Эйлера (Рис.4.): y_E=y_i+h×f(x_i, y_i).

В точке E вычисляют направление проходящей через нее интегральной кривой f_E=f(x_i+1,y_E).

В качестве окончательного значения направления кривой на всем отрезке h принимают среднее арифметическое значение от направлений f(x_i , y_i) и f_E , т.е. ординату точки A_i+1 вычисляют по формуле

.

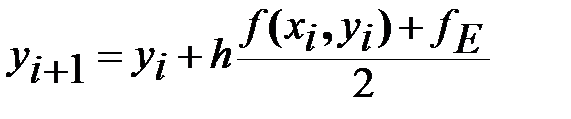Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки A_i+1:

.

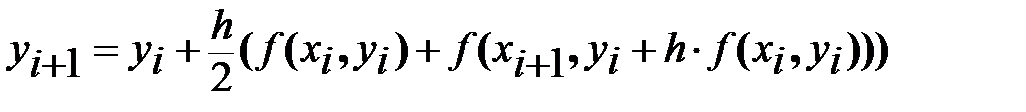Локальная погрешность обоих модифицированных методов О(h³) , глобальная - О(h²) .

Все методы Эйлера являются явными и одношаговыми , поскольку для вычисления последующего приближения необходимо знать только значение функции f(x,y) на предыдущем шаге.

Вопрос 19.Метод Рунге-Кутты.

 

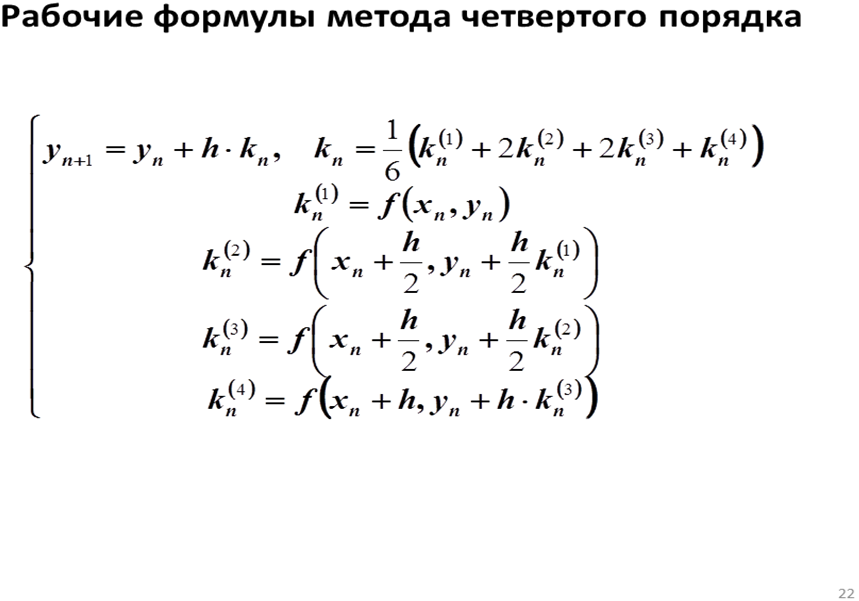
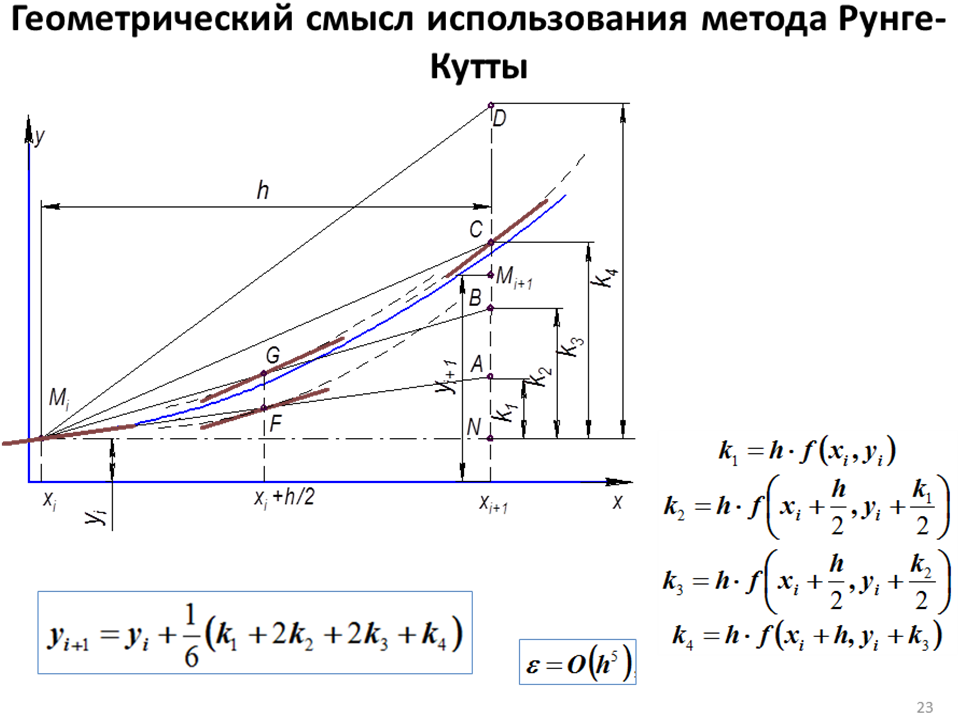
1. Из точки M_i с координатами (x_i,y_i) строят касательную в направлении, определяемым углом α₁ , для которого tg α₁=f(x_i,y_i) и находят точку A.

Расстояние NA будет k₁= hf(x_i,y_i).

2. При x=x_i+h/2 в точке F вычисляют наклон второй касательной с углом α₂ (касательная показана утолщенным отрезком) tg α₂=f(x_i+h/2,y_i+k₁/2). С этим наклоном проводят прямую из точки M_i и получают точку B .

При этом приращение будет NBk₂=hf(x_i+h/2,y_i+k₁/2).

3. Также при x=x_i+h/2, но уже в точке G пересечения прямой M_i B с одной из кривых семейства, вычисляют ее наклон (касательная показана утолщенным отрезком) как tgα₃=f(x_i+h/2 , y_i+k₂/2). С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение NC, равное k₃=hf(x_i+h/2,y_i+k₂/2).

Второй и третий этапы представляют не что иное, как модифицированные методы Эйлера.

4. При x=x_i+1 в точке С пересечения прямой M_iC с одной из кривых семейства вычисляют ее наклон (касательная также показана утолщенным отрезком) как tgα₄=f(x_i+h , y_i+k₃). С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение ND, равное k₄=hf(x_i+h,y_i+k₃).

5. Окончательно приращение ординаты точки M_i+1 вычисляют как средневзвешенную величину приращений k₁, k₂, k₃, k₄ , с весовыми коэффициентами 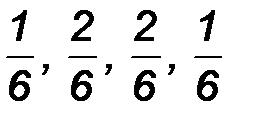соответственно

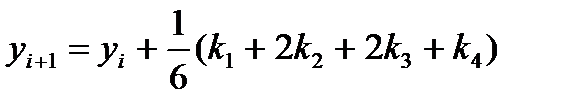
Где k₁= hf(x_i,y_i).

k₂=hf(x_i+h/2,y_i+k₁/2).

k₃=hf(x_i+h/2,y_i+k₂/2).

k₄=hf(x_i+h,y_i+k₃).

 

 

Вопрос 20.Численные методы решения задачи Коши для системы ОДУ первого порядка.

Определение :

Система дифференциальных уравнений называется нормальной , если все уравнения системы разрешены относительно старшей производной.

Рассмотрим систему ДУ вида :

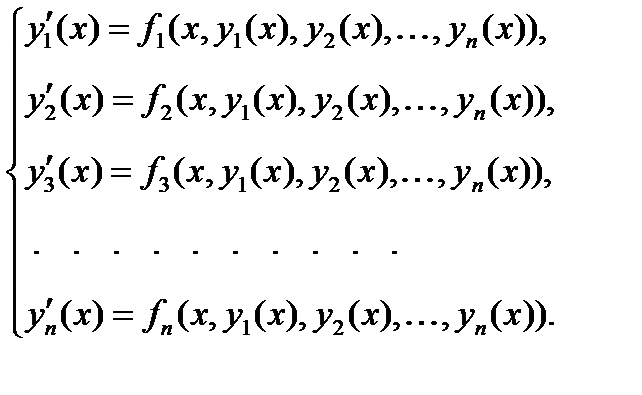
- искомые функции на промежутке [x₀,X]

Заданы начальные условия :

Введем понятие вектор-функции :

, ,

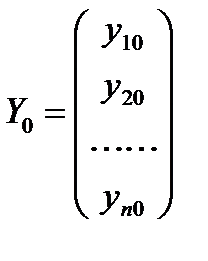
Тогда имеем :

 

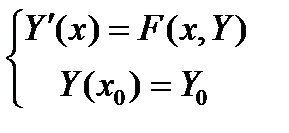
Вопрос 21. Решение ОДУ высших порядков.

 

Метод сеток

Вопрос 26.Задачи оптимизации. Линейное программирование.

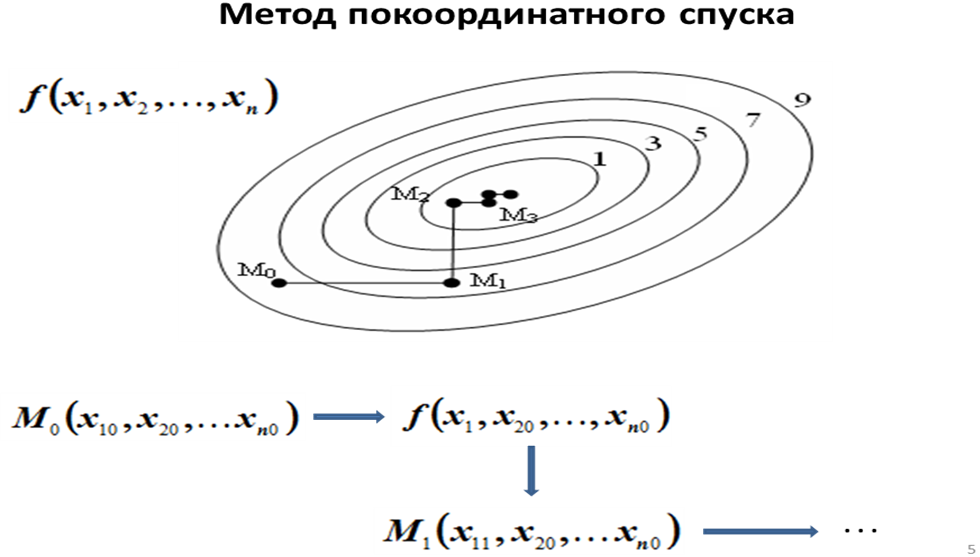
Линейное программирование

Вопрос 27.

Абсол. и относител. погрешности суммирования и вычитания чисел.