На рис. 4 показаны основные геометрические параметры конической зубчатой передачи.
Рис. 4 Геометрические параметры конической зубчатой передачи
Углы делительных конусов шестерни и колеса:
;
.
Делительные диаметры колес:
прямозубых 
; 
,
с круговым зубом 
; 
.
Внешние диаметры колес:
прямозубых 
,
,
с круговым зубом 
,
.
Диаметры впадин зубьев:
прямозубые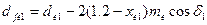 
,
,
с круговым зубом 
,
,
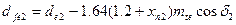средние диаметры 
, 
.
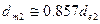Коэффициенты смещения хе и хn, для шестерни прямозубой и с круговым зубом принимают по табл. 3.16 и табл. 3.17.
Таблица 3.16
| z1 | xn1 при передаточном числе u | |||||||
| 1,0 | 1,25 | 1,6 | 2,0 | 2,5 | 3,15 | 4,0 | 5,0 | |
| – | – | – | – | 0,50 | 0,53 | 0,56 | 0,57 | |
| – | – | – | 0,44 | 0,48 | 0,52 | 0,54 | 0,55 | |
| – | – | 0,34 | 0,42 | 0,47 | 0,50 | 0,52 | 0,53 | |
| – | 0,18 | 0,31 | 0,40 | 0,45 | 0,48 | 0,50 | 0,51 | |
| – | 0,17 | 0,30 | 0,38 | 0,43 | 0,46 | 0,48 | 0,49 | |
| 0,00 | 0,15 | 0,28 | 0,36 | 0,40 | 0,43 | 0,45 | 0,46 | |
| 0,00 | 0,14 | 0,26 | 0,34 | 0,37 | 0,40 | 0,42 | 0,43 | |
| 0,00 | 0,13 | 0,23 | 0,29 | 0,33 | 0,36 | 0,38 | 0,39 | |
| 0,00 | 0,11 | 0,19 | 0,25 | 0,28 | 0,31 | 0,33 | 0,34 | |
| 0,00 | 0,09 | 0,15 | 0,20 | 0,22 | 0,24 | 0,20 | 0,27 |
Таблица 3.17
| z1 | xе1 при передаточном числе u | |||||||
| 1,0 | 1,25 | 1,6 | 2,0 | 2,5 | 3,15 | 4,0 | 5,0 | |
| – | – | – | 0,32 | 0,37 | 0,39 | 0,41 | 0,42 | |
| – | – | – | 0,30 | 0,35 | 0,37 | 0,39 | 0,40 | |
| – | – | 0,23 | 0,29 | 0,33 | 0,35 | 0,37 | 0,38 | |
| – | 0,12 | 0,22 | 0,27 | 0,31 | 0,33 | 0,35 | 0,36 | |
| – | 0,11 | 0,21 | 0,26 | 0,30 | 0,32 | 0,34 | 0,35 | |
| 0,00 | 0,10 | 0,19 | 0,24 | 0,27 | 0,30 | 0,32 | 0,32 | |
| 0,00 | 0,09 | 0,17 | 0,22 | 0,26 | 0,28 | 0,29 | 0,29 |
Продолжение таблицы 3.17
| 0,00 | 0,08 | 0,15 | 0,19 | 0,21 | 0,24 | 0,25 | 0,25 | |
| 0,00 | 0,07 | 0,11 | 0,16 | 0,18 | 0,21 | 0,22 | 0,22 | |
| 0,00 | 0,05 | 0,09 | 0,11 | 0,14 | 0,16 | 0,17 | 0,17 |
Для передач, у которых z1 и u отличаются от указанных в таблицах коэффициенты xе и хn принимают с округлением в большую сторону.
Размеры заготовки колес
Силы в зацеплении
Окружная сила на среднем диаметре шестерни, Н:
где dm1=0.875de1
Осевая сила на шестерне:
прямозубой 
с круговым зубом 
Радиальная сила на шестерне:
прямозубой 
с круговым зубом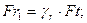 
Осевая сила на колесе 
Радиальная сила на шестерне 
.
Коэффициент γa и 
для угла βn = 35о определяют:
;
.
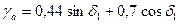Полученное значение γa и подставляют в формулы со своими знаками.
Проверка зубьев колес по контактным напряжениям
Значения величин входящих в формулу определены ранее. Фактические напряжения ( 
>[ 
]Н) не должны превышать 5 % от допускаемых.
Если условия прочности не выполняется, то следует увеличить de1, либо взять другие материалы и термообработку, пересчитать [ ]Н и повторить весь расчет передачи.
Проверка зубьев колес по напряжениям изгиба
;
где Ft,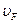 
, b, me(mte), 
, 
, 
, 
- определены ранее.
- коэффициенты формы зуба, определяют по табл. 3.18 в зависимости от эквивалентного числа зубьев шестерни 
и колеса 
:
для прямозубых колес:
для колес с круговыми зубьями:
,
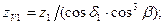
где 
=35о – угол наклона кругового зуба.
Таблица 3.18
Коэффициент формы зуба YF
| ZV | Коэффициент смещения режущего инструмента х | ||||||||||
| -0,5 | -0,4 | -0,3 | -0,2 | -0,1 | +0,1 | +0,2 | +0,3 | +0,4 | +0,5 | ||
| – – – – – 4,6 4,12 3,97 3,85 3,73 3,68 | – – – – 4,6 4,32 4,02 3,88 3,79 3,7 3,67 | – – – – 4,39 4,15 3,92 3,81 3,73 3,68 3,65 | – – – 4,55 4,2 4,05 3,84 3,76 3,7 3,65 3,62 | – – 4,5 4,28 4,04 3,9 3,77 3,7 3,66 3,62 3,61 | – – 4,27 4,07 3,9 3,8 3,7 3,65 3,63 3,61 3,6 | – 4,24 4,03 3,89 3,77 3,7 3,64 3,61 3,59 3,58 3,58 | – 3,83 3,75 3,67 3,62 3,58 3,57 3,56 3,56 3,57 | 3,9 3,78 3,67 3,61 3,57 3,55 3,53 3,53 3,53 3,54 3,55 | 3,67 3,59 3,53 3,5 3,48 3,47 3,48 3,49 3,5 3,52 3,53 | 3,46 3,42 3,4 3,39 3,39 3,4 3,42 3,44 3,46 3,5 3,52 |
Если при проверочном расчете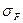 
значительно меньше [ ]F, это допустимо, т.к. нагрузочная способность передачи ограничивается контактной прочностью. Если 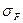>[ ]F свыше 5 %, то следует увеличить модуль 
, пересчитать z1 и z2 и повторить проверочный расчет на изгиб. При этом внешний делительный диаметр колеса de2 не изменяется, поэтому контактная прочность передачи не нарушается.
Проверка на прочность зубьев при действии пиковой нагрузки
где 
, Т – номинальный расчетный момент
Допускаемое напряжение 
принимают:
при улучшении и объемной закалке = 2,85 σт, цементации или поверхностной закалке ТВЧ = 44 HRCср.
где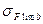 
– предел выносливости при изгибе (см. табл. 3.7);
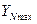- максимально возможное значение коэффициента долговечности:
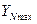= 4 для сталей с объемной термической обработкой (нормализация, излучения, обычная закалка);
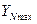= 2,5 для сталей с поверхностной обработкой: закалка ТВЧ, цементация, азотирование;
– коэффициент влияния частоты приложения пиковой нагрузки (в случае единичных перегрузок Kst = 1,2…1,3, при многократном действии перегрузок KSt = 1);
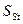- коэффициент запаса прочности (обычно 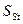= 1,75).
Расчет червячных передач
Допускаемые напряжения
Допускаемые напряжения [σ]н и [σ]F выбирают по рекомендациям раздела 3.3 и 3.5.
Межосевое расстояние
Условия зацепления и несущая способность червячных передач с архимедовыми, конволютными и эвольвентными червяками приблизительно одинаковы, вследствие чего формулы для расчета червячных передач с архимедовым червяком по ГОСТ19036-81 можно использовать и при расчете передач с другими червяками.
При расчете на контактную прочность определяют межосевое расстояние аw по формуле:
,
где аw – межосевое расстояние, мм;
Кa = 610 для эвольвентных, архимедовых и конволютных червяков;
Т2 – вращающий момент на валу червячного колеса, Н·м;
[σ]н – допускаемое контактное напряжение, МПа, (см раздел 3.3);
КНβ – коэффициент концентрации нагрузки:
КНβ = 1 при постоянном режиме нагружения,
КНβ = 0,5 (КНβо + 1) при переменном режиме нагружения;
Начальный коэффициент концентрации нагрузки КНβо находят по графику (рис. 6), для этого определяют число витков z1 червяка в зависимости от передаточного числа:
исвыше 8 до 14 свыше 14 до 30 свыше 30
z1 4 2 1
Рис. 6
Полученное значение межосевого расстояния округляют в большую сторону: для стандартной червячной пары до целого числа (мм): 50, 60, 70, 80, 100, 125, 140, 160, 180, 200, 225, 250, 280; для нестандартной до большего числа нормальных линейных размеров.
Основные параметры червячной передачи
Число зубьев колеса z2 = z1·и.
Предварительные значения:
модуля передачи 
;
коэффициента диаметра червяка 
.
В формулу для q подставляют ближайшее к расчетному стандарту значение m:
| m, мм | 2,5; 3,15; 4; 5 | 6,3; 8; 10; 12,5 | |
| q | 8; 10; 12,5; 16; 20 | 8; 10; 12,5; 14; 16; 20; | 8; 10; 12,5; 16 |
Полученное значение q округляют до ближайшего стандартного значения. Минимально допускаемое значение q из условия жесткости червяка 
;
Коэффициент смещения:
;
При этом должно выполняться условие -1 ≤ х ≤ 1.
Если это условие не выполняется, то следует варьировать значением q и z2, при этом 
, а z2 изменяют на 1 – 2 зуба, чтобы не превысить допускаемое отклонение передаточного числа ∆и.
Угол подъема линии витка червяка:
На делительном цилиндре 
;
На начальном цилиндре 
.
Фактическое передаточное число:
,
где и – заданное передаточное число.
Фактическое межосевое расстояние:
.
Размеры червяка и колеса
Далее определяют основные геометрические размеры передачи (рис. 7)
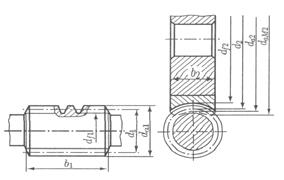
Рис. 7 Геометрические параметры червячной передачи.
При коррегировании исполнительные размеры червяка не изменяются; у червячного колеса делительный d2 и начальный dW2 диаметры совпадают, но изменяются диаметры вершинda2 и впадин df2.
Основные диаметры червяка, мм:
делительный диаметр 
;
начальный диаметр 
;
диаметр вершин витков 
;
диаметр впадин витков 
;
длина нарезной части червяка 
,
где х – коэффициент смещения. При х ≤ 0 С = 0; при х >0 С= 100·m/z2. Для шлифуемых и фрезеруемых червяков длину нарезной части b1 увеличивают на 25 мм при m < 10 и на 35 – 40 мм при m = 10 – 16 мм.
Основные размеры колеса, мм:
делительный диаметр 
;
диаметр вершин зубьев 
;
наибольший диаметр вершин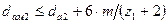 
;
диаметр впадин зубьев 
;
ширина венца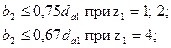 
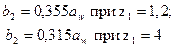
радиусы закруглений зубьев 
;
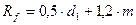
Условный угол обхвата червяка венцом колеса 2δ определяется точками пересечения дуги окружности диаметром 
с контуром венца колеса, как правило – это 90о – 120о и равен:
.
При этом должно выполняться условие: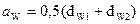 
Проверочный расчет
Уточняют КПД червячной передачи:
,
где γ – делительный угол подъема линии червяка;
ρ – угол трения, который определяется по табл. 3.19 в зависимости от скорости скольжения 
.
Таблица 3.19
Значения угла трения ρ
| Vs, м/с | ρ | Vs, м/с | β | Vs, м/с | ρ |
| 0,1 0,5 1,0 | 4о30' - 5о10' 3о10' - 3о40' 2о30' - 3о10' | 1,5 2,5 | 2о20' - 2о50' 2о00' - 2о30' 1о40' - 2о20' | 1о30' - 2о00' 1о20' - 1о40' 1о00' - 1о30' |
Примечание: Меньшие значения – для материалов группы I, большие для группы II и III см. (табл. 3.3).
Проверяют контактные напряжения зубьев колес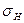 
, Н / мм2:
,
где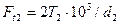 
- окружная сила на колесе, Н;
T2 – вращающий момент на колесе, Н·м;
, мм;
, мм;
К – коэффициент нагрузки, зависит от окружной скорости колеса 
, м/с: К = 1 при V ≤ 3 м / с; К = 1,1 – 1,3 при V > 3 м/с;
[σ]Н – допускаемое контактное напряжение зубьев колеса, Н/мм2, уточняется в зависимости от действительной скорости скольжения VS по зависимостям раздела 3.3.
Допускается недогрузка передачи ( <[ ] 
) не более 20 % и перегрузка ( >[ ] ) до 5 %. Если условия прочности не выполняется, следует выполнить другую марку материала венца червячного колеса (см. табл. 3.3) и повторить весь расчет передачи.
Определяют напряжения изгиба зубьев колеса σF, Н/мм2:
,
где YF2 – коэффициент формы зуба колеса, который выбирают по табл. 3.20 в зависимости от эквивалентного числа зубьев колеса 
. Здесь γ – делительный угол подъема линии витков червяка;
m – модуль зацепления, мм;
b2 – ширина венца червячного колеса, мм;
Ft2 – окружная сила на колесе, Н;
[σ]F – допускаемое напряжения изгиба, Н/мм2 (см. раздел 3.5)
K – коэффициент нагрузки: К = 1 при V ≤ 3 м/с; К = 1,1 – 1,3 при V > 3 м/с.
Таблица 3.20
Коэффициенты формы зуба YF2 червячного колеса
| ZV2 | YF2 | ZV2 | YF2 | ZV2 | YF2 | ZV2 | YF2 |
| 1,98 1,88 1,85 1,80 | 1,76 1,77 1,64 1,61 | 1,55 1,48 1,45 1,40 | 1,34 1,30 1,27 1,24 |
Рис. 8 Силы в зацеплении.
Силы в зацеплении
Окружная сила на колесе, равна осевой силе на червяке:
;
Окружная сила на червяке, равная осевой силе на колесе:
;
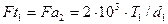Радиальная сила
,
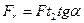где α = 200.
Тепловой расчет
Мощность (Вт) на червяке 
;
Температура нагрева масла (корпуса) без искусственного охлаждения.
,
Температура нагрева масла (корпуса) при охлаждении вентилятором.
,
где Ψ = 0.3 – коэффициент, учитывающий отвод тепла от корпуса редуктора в металлическую плиту или раму; 
– максимальная допустимая температура нагрева масла.
Поверхность охлаждения корпуса А, м2 равна сумме поверхностей всех его стенок, за исключением поверхности дна, которой корпус прилегает к плите или раме. Размеры стенок корпуса можно взять по эскизному проекту редуктора или приближенно в зависимости от межосевого расстояния.
аw, мм… 80 100 125 140 160 180 200 225 250 280
А, м2 … 0,16 0,24 0,35 0,42 0,53 0,65 0,78 0,95 1,14 1,34
Для чугунных корпусов при естественном охлаждении коэффициент теплоотдачи Кт = 12…18, Вт/м2 (большие значения при хороших условиях охлаждения).
Коэффициент Ктв при обдуве вентилятором.
nВ… .750 1000 1500 3000
КТВ…20 24 35 50
Здесь nВ – частота вращения вентилятора, мин-1.
Вентилятор обычно устанавливают на валу червяка.
Дата: 2016-10-02, просмотров: 220.
