Для определения основных статистических показателей с достаточной точностью необходима какая-то минимальная выборка. Ее объем рекомендуется определить до начала наблюдений. Достаточный объем выборки определяют по формуле

где N - искомый объем выборки;

t - критерий достоверности (в зависимости от доверительного уровня исследования t=1,96 при P1=0,95; t=2,58 при P2=0,99; t=3,30 при P3=0,999);

V - вариация (изменчивость признака);

P - заданная ошибка опыта.

Если известна вариация изучаемого признака, ее величину подставляют в формулу, если нет, то вариацию принимают за 50%. Иначе можно применить таблицы достаточно больших чисел и количество наблюдений в начале работы рассчитать по ним. В дальнейшем потребуется корректировка количества наблюдений в соответствии с полученными результатами.

Показатели меры связи

Причина и следствие. Эти два понятия связаны между собой теснейшим образом. Причинный признак называется независимой переменной (аргументом) и обозначается «Х», а следствие (функция) обозначается латинской буквой «Y». В биологических явлениях связь чаще всего коррелятивная - каждому значению переменной Х может соответствовать несколько значений Y.

Наиболее короткий путь исследования зависимости (в смысле затраты времени) - отражение ее сначала на графике. Если связь просматривается и близка к прямолинейной, то вычисляют коэффициент корреляции (r). Он показывает степень приближения связи к функциональной и может быть в пределах от +1 до -1. Если r =1 или -1, связь функциональная.

При r =0 еще нельзя говорить об отсутствии связи. Эта связь может быть не прямолинейной, а криволинейной.

Коэффициент корреляции вычисляется по формуле

или

где r - коэффициент корреляции; x_i- варианты ряда аргумента; y_i варианты ряда функции; N - объем выборки; - среднее по функции.

При большом показателе r можно попытаться найти уравнение связи между x и y.

Иногда изучают связь некоторого признака не с одним, а с двумя факторами, совместно влияющими на него. Взаимодействие факторов может как усиливать, так и ослаблять влияние на признак. В этом случае устанавливают действительную тесноту связи признака с одним фактором при исключении другого. Для этой цели применяют частные коэффициенты корреляции:

где - полные (обычные) коэффициенты корреляции между признаками;

- частные коэффициенты корреляции при исключенном влиянии третьего признака, указанного через точку.

По величине r можно установить характер связи:

При слабой связи, когда коэффициент корреляции близок к нулю, можно вычислить корреляционное отношение . Корреляционное отношение служит для оценки силы связи между двумя признаками, когда последние могут быть не только в прямолинейной, но и в криволинейной зависимости между собой; при более детальном исследовании вместо корреляционных отношений лучше применить методы дисперсного анализа.

Корреляционное отношение может вычисляться по алгоритму Н.А.Плохинского [10] или в Excel.

Иногда возникают вопросы отбора двух и более факторов, с которыми изучаемое явление или признак связаны наиболее тесно. Отбор таких факторов является самым простым. При увеличении количества факторов объем вычислений становится большим, а сам метод уже называется факторным анализом.

Степень связи значений одного признака одновременно со значением двух других устанавливают при множественных коэффициентах корреляции по формулам:

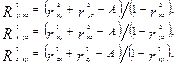
где 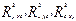- множественные коэффициенты корреляции; точка после y означает, что изучается совместное влияние аргументов x и z на функцию y.