Проблема минимизации логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них оптимальной (минимальной). Существует большое количество методов минимизации ЛФ. Все они отличаются друг от друга спецификой применения операций склеивания и поглощения, а также различными способами сокращения переборов. Среди аналитических методов наиболее известным является метод Квайна — Мак Класки, среди табличных — метод с применением диаграмм Вейча [6]. Графические методы минимизации отличаются большей наглядностью и меньшей трудоемкостью, однако их применение эффективно при малом числе переменных n≤5.
Рассмотрим последовательность действий минимизации ЛФ на примере.
Пример 2.15.Найти минимальную дизъюнктивную форму функции, заданной таблицей истинности (табл. 2.6).
Таблица 2.6 Таблица истинности функцииУ=f(x1, x2,x3)
| Х1 | Х2 | Xз | Y |
Эта функция интересна тем, что имеет несколько минимальных форм. По данным таблицы запишем аналитическое выражение: 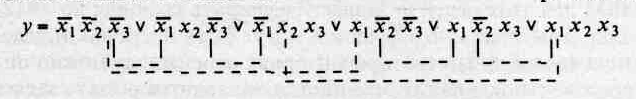
Пунктирными линиями в этом выражении отмечены пары конъюнкций, к которым можно применить операцию склеивания типаFxVFx=F. Особенно хорошо это видно при использовании диаграммы Вейча, в которой «склеиваемые» конъюнкции находятся по соседству друг с другом. Диаграмма Вейча просто по-другому интерпретирует таблицу истинности (табл. 2.7).
Задание.
Три человека участвуют в тайном голосовании. Составить логическую схему, регистрирующую результаты тайного голосования большинством голосов.
Пусть А – первый человек, голосующий «за», В – второй человек, голосующий «за» и С – третий человек, голосующий «за». Составим таблицу истинности интересующего нас итогового высказывания F (предложение принимается большинством голосов).
Таблица истинности.
| A | B | C | F | Ответ |
| - | ||||
| - | ||||
| - | ||||
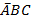
| ||||
| - | ||||
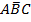
| ||||
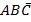
| ||||

|
Искомое высказывание имеет вид:

После упрощения функция принимает вид:

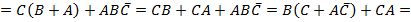
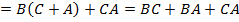
Таким образом, логическая схема, реализующая процесс голосования, будет иметь вид:
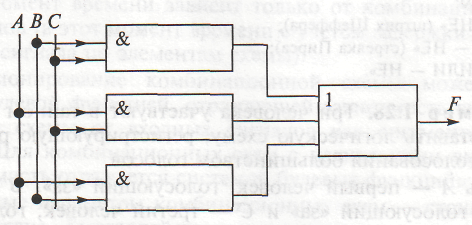
Пример 1. Аня, Вика и Сергей решили пойти в кино. Классный руководитель, хорошо знавший этих ребят, высказал следующие предположения:
а) Аня пойдет в кино только тогда, когда пойдут Вика и Сергей;
б) Аня и Сергей пойдут в кино вместе или же оба останутся дома;
в) для того чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что классный руководитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из названных ребят пошел в кино? Решить задачу с помощью логических операций.
высказывания, описывающие приведенные в условии задачи факты, имеют вид:
Пример 2На вопрос, какая погода будет завтра, синоптик ответил:
а) если не будет ветра, то будет пасмурная погода без дождя;
б) если будет дождь, то будет пасмурно и без ветра;
в) если будет пасмурная погода, то будет дождь и не будет ветра
Подумав немного, синоптик уточнил, что три его высказывания можно лаконично записать в виде одного составного высказывания. Сформулируйте его, решив задачу с помощью логических операций.
Пример 3 Миша решил поступить в МИЭТ и послал домой три сообщения:
• если я сдам математику, то информатику я сдам только при условии, что не получу двойку за диктант;
• не может быть, чтобы я получил двойки за диктант и математику;
• достаточное условие провала по информатике — это двойка за диктант.
После сдачи экзаменов оказалось, что из трех Мишиных сообщений только одно было ложным. Как Миша сдал экзамены? Решить задачу с помощью логических операций.
Пример 5Проверьте правильность следующего умозаключения. Для того чтобы Саша прошел по конкурсу в МИЭТ, достаточно, чтобы или Аня, или Вика не прошли по конкурсу в институт. Вика пройдет по конкурсу вместе с Димой. Не может быть, чтобы по конкурсу прошли и Аня, и Саша.
Вывод. Для того чтобы Аня прошла по конкурсу в институт, необходимо, чтобы по
конкурсу прошли Дима и Саша
Пример 6
Задание. Три человека участвуют в тайном голосовании. Составить логическую схему, регистрирующую результаты тайного голосования большинством голосов.
Пример 7 Определить, кто из абитуриентов A, B, C, D играет, а кто не играет в шахматы, если известно следующее:
1) Если A или B играет, то C не играет;
2) Если B не играет, то играют C и D:
3) C – играет в шахматы.
Пример 8Дано суждение «или верно, что Петр поступил в университет (А), и при этом неверно, что Петр не поступил и Андрей не поступил, или Петр поступил и Семен поступил (С), или даже Петр поступил, и Семен поступил, и Андрей поступил (В)». Кто поступил в университет?
Пример 9.Шесть школьников – Андрей, Борис, Григорий, Дмитрий, Евгений и Семен- участвовали в олимпиаде. Двое из них решили все задачи.
На вопрос, кто решил все задачи, последовали ответы: 1) Андрей и Дмитрий; 2)Борис и Евгений; 3) Евгений и Андрей; 4) Борис и Григорий; 5) Семен и Андрей.
В четырех из этих ответов одна часть неверна, другая верна. В одном обе части неверны. Кто решил все задачи?
Контрольные вопросы:
1. Что такое ранг элементарной конъюнкции?
2. Как определяется длина ДНФ?
3. Дайте определение совершенной дизъюнктивной нормальной форме (СДНФ)?
4. В чем особенность расчетного метода (метода непосредственных преобразований)
5. Какая функция называется импликантной?
6. В чем сущность геометрической интерпретации области определения булевой
функции?
Лабораторная работа 3
Программирование разветвляющегося процесса
Задание 1
Цель работы:
Архитектура ЭВМ и система команд.
Дата: 2016-10-02, просмотров: 409.