Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Организация вычислительных систем и сетей

Методические указания к выполнению лабораторных работ

для студентов всех форм обучения

специальности 5В070400– «Вычислительная техника и программное обеспечение»

 

Алматы -2012

СОСТАВИТЕЛИ: Т.Т. Коржымбаев, Г.С. Нурмагамбетов «Организация вычислительных систем и сетей»

 

Методические указания к выполнению лабораторных работ для студентов всех форм обучения специальности 5В070400 – «Вычислительная техника и программное обеспечение». – Алматы: АИЭС, 2012. – 65 с

 

Методические указания предназначены для выполнения в компьютерном классе лабораторных работ по дисциплине «Организация вычислительных систем и сетей». Для каждой лабораторной работы даны краткие методические указания и упражнения для индивидуального выполнения. Перед выполнением лабораторной работы студент должен ознакомиться с методическими указаниями, изучить материалы по соответствующей теме и ответить на контрольные вопросы. После завершения лабораторной работы студент обязан представить преподавателю отчет в электронном виде.

Методические указания предназначены для студентов специальности 5В070400 – «Вычислительная техника и программное обеспечение» всех форм обучения.

Библиография – 6 назв.

 

Рецензент: канд. техн. наук. доц. Б.М.Шайхин

 

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2012 г.

 

 

© НАО «Алматинский институт энергетики и связи» на 2012 г.

 

Содержание

 

1 Лабораторная работа № 1.

Разработка алгоритма и микропрограммы арифметической операции над

числами с фиксированной ,плавающей точкой и двоично-десятичными

кодами.

 

2 Лабораторная работа № 2.

Исследование логических основ цифровых автоматов.

3 Лабораторная работа № 3.

Программирование

разветвляющегося процесса.

Система команд

 

4 Лабораторная работа № 4.

Исследование конвейерной обработки

5 Лабораторная работа № 5

Подпрограммы и стек

6 Лабораторная работа № 6

Программирование внешних устройств

 

7 Лабораторная работа № 7

Изучение программы PacketTracer . Изучение интерфейса командной

Строки Cisco IOS.

 

8 Лабораторная работа № 8

Изучение орбит ИСЗ с помощью программы “Orbitron”

 

Лабораторная работа №1

Разработка алгоритма и микропрограммы арифметической операции над числами с фиксированной ,плавающей точкой и двоично-десятичными кодами.

Цель работы:Произвести операции сложения являющихся базовой с использованием машинных кодов с использованием программной модели АЛУ.

Теоретическая часть

Набор арифметических операций составляют операции сложения, вы­читания, умножения и деления. Операция сложения является ба­зовой, так как она входит в состав операций умножения и деле­ния, а вычитание вообще выполняется как сложение с учетом знаков операндов (при использовании машинных кодов).

Алгоритм сложение целых двоичных чисел с ФТ производится в следу­ющем порядке:

1. Операнды представляются в обратном или дополнительном коде. Обычно используют ДК.

2. Сложение операндов производится поразрядно, начиная с младшего разряда.

3. В каждом разряде выполняются сложение двух цифр слагаемых и перенос из младшего разряда в соответствии с правилами двоичной арифметики.

4. Знаковые разряды участвуют в сложении наряду с цифровыми разрядами. Знак результата получается автоматически.

5. При сложении чисел в ДК перенос из знакового разряда отбрасывается. (При сложении чисел в ОК перенос из знакового разряда прибавляется к младшему разряду суммы.)

6. Если слагаемые представлены в ДК, то результат сложения получается также в ДК.

7. При сложении чисел с одинаковыми знаками возможно пе­реполнение разрядной сетки.

 

Сложение и вычитание чисел с ПТ. Особенностью сложения и вычитания чисел с ПТ является то, что в общем случае операнды могут иметь различные порядки. Суммировать разряды мантиссы можно только тогда, когда они имеют одинаковый вес, поэтому перед суммированием мантисс необходимо выровнять порядки. При этом могут быть потеряны младшие разряды мантиссы. Для уменьшения погрешности выполняется округление результата. После суммирования результат может оказаться ненормализован­ным, в этом случае необходима его нормализация.

С учетом этих особенностей сложение чисел с ПТ выполняется : в следующем порядке: подготовительный этап, выравнивание порядков, сложение мантисс, заключительный этап.

Алгоритм сложение целых двоичных чисел с ПТ производится в следу­ющем порядке:

1) Сравниваются порядки (характеристики) исходных чисел путем их вычитания Δ p=p₁-p₂ . При выполнении этой операции определяется, одинаковый ли порядок имеют исходные слагаемые.

2) Если разность порядков равна нулю, то это значит, что одноименные разряды мантисс имеют одинаковые веса (двоичный порядок). В противном случае должно проводиться выравнивание порядков.

3) Для выравнивания порядков числа с меньшим порядком сдвигается вправо на разницу порядков Δ p. Младшие выталкиваемые разряды при этом теряются.

4) После выравнивания порядков мантиссы чисел можно складывать (вычитать) в зависимости от требуемой операции. Действия над слагаемыми производятся в обратном или дополнительном коде по общим правилам.

5) Порядок результата берется равным большему порядку.

6) Если мантисса результата не нормализована, то осуществляются нормализация и коррекция значений порядка.

Задание 1

Пример 1. Сложить числа А₁₀ = -2 и В₁₀ = -9 с одинаковыми знаками (без

переполнения).

А₂= − 0010→ А₂^пк = 1 0010→ А₂^ок =1 1101→ А₂^дк= 1 1110

+ +

В₂= −1001→ В₂^пк = 1 1001→ В₂^ок = 1 0110→ В₂^дк =1 0111

А₂ ^дк +В₂^дк= С₂^дк = 11 0101→ С₂^пк =1 1011;

С₂ = −1011, С₁₀=−11.

При сложении чисел с одинаковыми знаками возможно по­лучение результата, значение которого больше величины 2^n-1, где n — разрядность слагаемых. При этом результат не укладывается в отведенных для него разрядах, поэтому такая ситуация называет­ся переполнением разрядной сетки.

 

Пример 2. Сложить числа А₁₀ = -13 и В₁₀ = -6 с одинаковыми знака­ми (с переполнением).

А₂ = −1101 → А₂^пк = 1 1101→ А₂^ок = 1 0010 → А₂^дк = 1 0011

+ +

В₂ = -0110 → В₂^пк = 1 0110 → В₂^ок = 1 1001 → В₂^дк = 1 1010

А₂ ^дк +В2^дк= С₂^дк= 10 1101→С₂^пк =0 1101;

С₂ = + 1101, С₁₀=+13.

Одним из признаков переполнения является отличие знака суммы от знака слагаемых. Иногда при сложении используется модифицированный дополнительный код (МДК), в котором для знака числа отводится два разряда. В этом случае признаком пере­полнения являются различные значения знаковых разрядов сум­мы. Если переполнение не возникает, то значения знаковых раз­рядов совпадают. Рассмотрим примеры сложения чисел в МДК.

Пример 3. Сложить числа А₁₀ = +11 и В₁₀ = +8 (сумма больше 0).

А₂= + 1011→ А₂^пк = 0 1011 → А₂^ок = 0 1011 → А₂^мдк = 00 1011

+ +

В₂ =+ 1000 → В₂^пк = 0 1000 → В₂^ок = 0 1000 → В₂^мдк = 00 1000

 

А₂ ^дк +В₂^дк = С₂^мдк = 01 0011

Переполнение! Различные значения знаковых разрядов суммы.

 

Так как при сложении в дополнительном коде учитываются знаки чисел, то вычитание чисел можно заменить сложением в соответствии с соотношением

А-В = А + (–В).

Таким образом, вычитание заменяется сложением уменьшае­мого с вычитаемым, взятым с обратным знаком.

 

Пример 4. Произвести вычитание чисел А₁₀= −3 и B₁₀ = +15 (с пере­полнением).

А₂= − 0011→ А₂^пк= 1 0011 → А₂^ок=1 1100→ → → → → А₂^дк= 1 1101

+ +

В₂=+1111 → В₂^пк= 0 1111→ (− В)₂^пк = 1 111→ (− В)₂^ок=1 0000 →

→ (− В)₂^дк =1 0001

______

А₂ ^дк +В₂^дк= С₂^дк= 10 1110;

С₂^пк = 0 1101 С₂=+1101? Переполнение!

Признаком переполнения в данном случае являются различные зна­чения знаковых разрядов разности.

 

Задание 2

Пример 5. Выполнить сложение чисел с ПТ в ДК, если А₁₀ = −15⁵/₈;

А₂ =−1111.101; А_ПТ = −0.1111101х10⁺¹⁰⁰.

В₁₀ = + 16¹/₄; В₂ = +10000.01; В_ПТ =+0.1000001х10⁺¹⁰¹ .

(М_А)^пк= 1 1111101; (М_А)^дк = 1 0000011; (Р_А)^пк=0 100; (Р_А)^дк= 0 100; (М_В)^пк =

0 1000001; (М_В)^дк = 0 1000001;

(Р_В)^ПК = 0 101; (Р_В)^дк = 0 101; (−Р_В)^дк=1 011.

Вычислим разность порядков:

(Р_А)^ДК = 0 100

+

(−Р_В )^дк=1 011

______________

(ΔР)^ДК = 1 111 →(ΔР)^ПК =1 001→ (ΔР)₂ =−001→(ΔР)₁₀ =−1.

Разность порядков не равна нулю, выравнивание порядков необхо­димо. Разность порядков меньше нуля, число А имеет меньший порядок. Сдвигается мантисса числа А.

Мантисса числа А после сдвига: (М_А)^дк = 1 1000001 |1.

(В освобождающиеся разряды мантиссы заносится значение знаково­го разряда. Старший из выдвигаемых разрядов сохраняется в дополни­тельном разряде регистра суммы.)

Порядок суммы (Р_А+В)^ДК = (Р_В)^ДК = 0 101.

Выполним сложение мантисс: (М_А)^дк = 1 1000001 |1

+

(М_в)^дк = 0 1000001 |0

___________

(М_А)^дк+ (М_В)^дк= (М_А + М_В)^дк = 10 0000010 |1. Нормализация наруше­на справа.

Мантисса суммы сдвигается влево на пять разрядов.( не влево а вправо от сидящего)

 

Мантисса суммы после сдвига: (М_А + М_В)^дк = 0 1010000 |0

Округление. + |1

=___________

Мантисса суммы после округления: (М_А + М_В)^дк = 0 1010000.

Порядок суммы после нормализации: (Р_А+В)^ДК = 0 101 + 1 011=0 000. Результат: (М_А + М_В)^пк = 0 1010000 → (М_А + М_В)₂ = + 0.1010000.

(Р_А+В)^ДК = 0 000 → (Р_А+В)₂ = + 000.

Сумма: (А + В)_ПК = +0.1010000 х 10⁺⁰⁰⁰ →(А + В)₂ = +0.101 →(А+В)₁₀ =+⁵/_8.

Точный результат: −15⁵/₈ + 16¹/₄ = +⁵/_8.

При выполнении операции вычитания знак вычитаемого изменяется на противоположный, далее операция продолжается как сложение.

 

Пример 6. Определить разность чисел, представленных в форме с ПТ. Операцию выполнить с использованием МДК.

А₁₀ = −5³/₄; А₂ =−101.11; А_пт = −0.10111х10⁺⁰¹¹.

В₁₀ = + 3⁵/₈; В₂ = +11.101; В_пт =+0.11101х10⁺⁰¹⁰ .

(М_А)^пк= 1 10111; (М_А)^мдк = 11 01001; (Р_А)^пк=00 011; (Р_А)^мдк= 00 011; (М_В)^пк =

0 11101; (М_В)^мдк =00 11101; (−М_В)^мдк = 11 00011.

(Р_В)^пк = 00 010; (Р_В)^мдк = 00 010; (−Р_В)^мдк=11 110.

Вычислим разность порядков:

(Р_А)^мдк = 00 011

+

(−Р_В )^мдк=11 110

________

(ΔР)^мдк = 00 001 →(ΔР)^пк =00 001→ (ΔР)₂ =+001→ΔР)₁₀ =+1.

Разность порядков не равна нулю, выравнивание порядков необхо­димо. Разность порядков больше нуля, число В имеет меньший порядок. Сдвигается мантисса числа В.

Мантисса числа (−В) после сдвига: (−М_В)^мдк =11 10001|‌1.

Порядок разности (Р_А-В)^мдк = (Р_А)^мдк = 00 011.

Выполним сложение мантисс: (М_А)^мдк =11 01001|0

+

(−М_В)^мдк= 11 10001|1

___________________

(М_А)^мдк + (−М_В)^мдк= (М_А − М_В)^мдк = 0 11010|1. Нормализация на­рушена слева.

Мантисса разности сдвигается вправо на один разряд.
Мантисса разности после сдвига: (М_А − М_В)^мдк = 11 01101|0
Округление. + |1

_______________________

Мантисса разности после округления: (М_А − М_В)^мдк =11 01101.

Порядок разности после нормализации: (Р_А-В)^мдк = 00 011 + 00 001 =

= 00 100.

Результат: (М_А – М_В)^пк = 11 10011 → (М_А − М_В)₂ = −0.10011.

(Р_А-В)^МДК = 0 100 → (Р_А-В)₂ = +100.

(А − В)_ПТ = −0.10011 х 10⁺¹⁰⁰ → (А- В)₂ = −1001.1 →(А− В)₁₀ = −9¹/₂.

Точный результат: −5³/₄ − 3⁵/₈ = −9³/_8.

Погрешность возникла при

сдвиге мантиссы числа В при выравнива­нии порядков.

Задание 3

Пример 7.Сложить два числа А_ю= 177; В₁₀=418.

 

 

Пример 8

Определить сумму чисел в двоично-десятичном коде, если

А₁₀ = –183; B10 = 924.

A_2–10 = – 0001 1000 0011; B_2–10 = + 1001 0010 0100

(A_2–10)^ПК = 1 0001 1000 0011 (B_2–10)^пк = 0 1001 0010 0100

+ 0110 0110 0110 Прибавление кода 0110

(A_2–10)^ОК = 1 0111 1110 1001

1 1000 0001 0110 Инверсия

+ 0001 Прибавление единицы

(A_2–10)^ДК = 1 1000 0001 0111 (B_2–10)^ДК = 0 1001 0010 0100

(B _2–10)^ДК = + 0 1001 0010 0100 Сложение

(A_2–10 + B _2–10)^ДК=10 0001 0011 1011 При суммировании возник

коррекция + 0110 0110 перенос из первой тетрады

(A_2–10 + B _2–10)^ДК= 0 0111 0100 0001 и образовалась запрещенная

(A +B) _2–10 = + 0111 0100 0001 комбинация последней тетраде

(A +B) ₁₀ = + 741

 

Варианты индивидуальных заданий. Индивидуальное задание студенту определяется преподавателем. В индивидуальном задании требуется произвести операций над числами с ФТ, ПТ и Двоично-десятичном коде.

Вариант к заданию 1

 

А0		− 9	−2	−12	−11			−4
В0	−7		−9	−6			−3		−4

 

Вариант к заданию 2

А0	-145/8	125/8	1105/8	115/8	155/8	165/8	195/8	185/8	175/8
В 0	151/4	171/4	111/4	141/4	131/4	161/4	191/4	181/4	121/4

 

Вариант к заданию 3

 

А0	-214		-172		-174		-167	-174
В0		-171		-123		-387			-768

 

 

Контрольные вопросы

 

1. Какие элементы формата чисел с ПТ вы знаете?

2. Чем отличается нормализованное число с ПТ от

ненормализованного числа?

3. Для чего применяются двоично-десятичные коды?

4. Как зависит разрядность чисел от величины основания системы счисления?

5. Можно ли различить форматы целых и дробных чисел с ФТ?

6. Для чего используются машинные коды чисел?

7. Чем отличаются дополнительный и обратный коды отрицательных чисел?

8. Как из ДК отрицательного числа получить ПК числа?

 

 

Лабораторная работа 2

Законыалгебры логики

Из определения вышеприведенных функций можноустановить целый ряд простейших свойств:

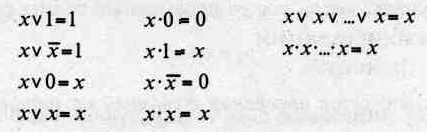
В алгебре логики установлен целый ряд законов, с помощью которых возможно преобразование логических функций (ЛФ):

• коммутативный (переместительный):

• ассоциативный (сочетательный):

Эти законы полностью идентичны законам обычной алгебры;

• дистрибутивный (распределительный):

• закон поглощения. В дизъюнктивной форме ЛФ конъюнкция мень­шего ранга, т.е. с меньшим числом переменных, поглощает все конъ­юнкции большего ранга, если ее изображение содержится в них. Это же справедливо и для конъюнктивных форм:

• законы склеивания:

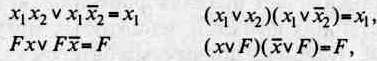
где F — логическая функция общего вида, не зависящая от переменной х;

• закон свертки:

• правило де Моргана:

Убедиться в тождественности приведенных зависимостей мож­но путем аналитических преобразований выражений или путем по­строения таблицы истинности для ЛФ, находящихся в левой и пра­вой частях. Используя данные зависимости, можно преобразовывать исходные выражения в более простые (минимизировать их). По упрощенным выражениям можно построить техническое устройство, имеющее ми­нимальные аппаратные затраты.

Пример 6

Задание. Три человека участвуют в тайном голосовании. Составить логическую схему, регистрирующую результаты тайного голосования большинством голосов.

Пример 7 Определить, кто из абитуриентов A, B, C, D играет, а кто не играет в шахматы, если известно следующее:

1) Если A или B играет, то C не играет;

2) Если B не играет, то играют C и D:

3) C – играет в шахматы.

Пример 8Дано суждение «или верно, что Петр поступил в университет (А), и при этом неверно, что Петр не поступил и Андрей не поступил, или Петр поступил и Семен поступил (С), или даже Петр поступил, и Семен поступил, и Андрей поступил (В)». Кто поступил в университет?

 

Пример 9.Шесть школьников – Андрей, Борис, Григорий, Дмитрий, Евгений и Семен- участвовали в олимпиаде. Двое из них решили все задачи.

На вопрос, кто решил все задачи, последовали ответы: 1) Андрей и Дмитрий; 2)Борис и Евгений; 3) Евгений и Андрей; 4) Борис и Григорий; 5) Семен и Андрей.

В четырех из этих ответов одна часть неверна, другая верна. В одном обе части неверны. Кто решил все задачи?

Контрольные вопросы:

1. Что такое ранг элементарной конъюнкции?

2. Как определяется длина ДНФ?

3. Дайте определение совершенной дизъюнктивной нормальной форме (СДНФ)?

4. В чем особенность расчетного метода (метода непосредственных преобразований)

5. Какая функция называется импликантной?

6. В чем сущность геометрической интерпретации области определения булевой

функции?

Лабораторная работа 3

Программирование разветвляющегося процесса

Задание 1

Цель работы:

Архитектура ЭВМ и система команд.

Пример 1

Дана последовательность мнемокодов, которую необходимо преобразовать в машинные коды, занести в ОЗУ ЭВМ, выполнить в режиме Шаг и зафикси­ровать изменение состояний программно-доступных объектов ЭВМ (табл. 1).

Таблица 1.Команды и коды

 

Последовательность	Значения
Команды	RD#20	WR30	ADD #5	WR@30	JNZ 002
Коды	21 1 020	22 0 030	23 1 005

 

Введем полученные коды последовательно в ячейки ОЗУ, начиная с адреса 000. Выполняя команды в режиме Шаг, будем фиксировать изменения про­граммно-доступных объектов (в данном случае это Асc, РС и ячейки ОЗУ 020 и 030) в табл.2.

Таблица 2.Содержимое регистров

 

РС	Асе	М(30)	М(20)	РС	Асе	М(30)	М(20)

Выполнение работы

1.Ознакомиться с архитектурой ЭВМ

2. Записать в ОЗУ "программу", состоящую из пяти команд — варианты задания выбрать из табл. 3. Команды разместить в последовательных ячейках памяти.

3. При необходимости установить начальное значение в устройство ввода IR.

4. Определить те программно-доступные объекты ЭВМ, которые будут изменяться при выполнении этих команд.

5. Выполнить в режиме Шагвведенную последовательность команд, фиксируя изменения значений объектов, определенных в таблице (см.
форму табл.2).

6. Если в программе образуется цикл, необходимо просмотреть не более двух повторений каждой команды, входящей в тело цикла.

 

Задание 2

 

Цель работы

Программирование разветвляющегося процесса

 

Пример 1

В качестве примера рассмотрим программу вычисления функции

(х-11)²-125, при х≥6,

х2 +72*-6400

У , при x<16,

-168

 

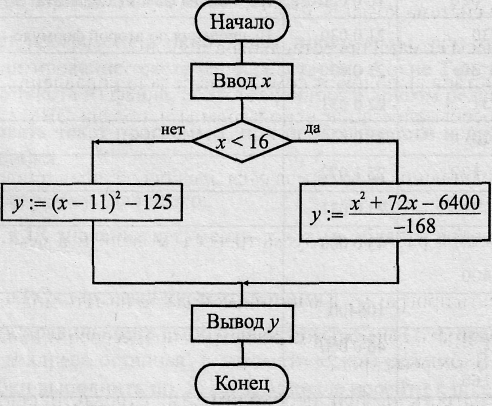
причем х вводится с устройства ввода IR, результат у выводится на OR. Граф-схема алгоритма решения задачи показана на рис. 1.

 

Рис. 1.Граф-схема алгоритма

 

данной лабораторной работе используются двухсловные команды с непо­средственной адресацией, позволяющие оперировать отрицательными чис­лами и числами по модулю, превышающие 999, в качестве непосредственно­го операнда.

Оценив размер программы примерно в 20—25 команд, отведем для области данных ячейки ОЗУ, начиная с адреса 030. Составленная программа с ком­ментариями представлена в виде табл. 1.

Таблица 1.Пример программы

 

Адрес	Команда	Примечание
	Мнемокод	Код
	IN	01 0 000	Ввод х
	WR 30	22 0 030	Размещение х в ОЗУ(ОЗО)
	SUB #16	24 1 016	Сравнение с границей — (х — 16)
	JS 010	13 0 010	Переход по отрицательной разности
	RD 30	21 0 030	Вычисления по первой формуле
	SUB #11	24 1 011
	WR 31	22 0 031
	MUL 31	25 0 03 1
	SUB #125	24 1 125
	JMP 020	10 0 020	Переход на вывод результата
	RD 30	21 0 030	Вычисления по второй формуле
	MUL 30	25 0 030
	WR 31	22 0 031
	RD 30	21 0 030
	MUL #72	25 1 072
	ADD 31	23 0 031
	ADI 10640000	43 0 000
	DIVI	46 0 000
	ОUT	02 0 000	Вывод результата
	HLT	09 0 000	Стоп

Задание 1

1. Разработать программу вычисления и вывода значения функции:

y = |Fi-(x), при х ≥ а,

Fj-(x), при х < а,

 

для вводимого из IR значения аргумента х. Функции и допустимые пре­делы изменения аргумента приведены в табл. 2, варианты заданий — в табл. 3.

2. Исходя из допустимых пределов изменения аргумента функций (табл. 2) и значения параметра а для своего варианта задания (табл. 3) выделить на числовой оси Ох области, в которых функция у вычисляется по представленной в п. 1 формуле, и недопустимые значения аргумента. На
недопустимых значениях аргумента программа должна выдавать на OR максимальное отрицательное число: 199 999.

3. Ввести текст программы в окно Текст программы,при этом возможен набор и редактирование текста непосредственно в окне Текст программыили загрузка текста из файла, подготовленного в другом редакторе.

4. Ассемблировать текст программы, при необходимости исправить синтак­сические ошибки.

5. Отладить программу. Для этого:

а) записать в IR значение аргумента х > а (в области допустимых значений);

б) записать в РС стартовый адрес программы;

в) проверить правильность выполнения программы (т. е. правильность ре­зультата и адреса останова) в автоматическом режиме. В случае нали­чия ошибки выполнить пп. 5, г и 5, д; иначе перейти к п. 5, е;

г) записать в РС стартовый адрес программы;

д)наблюдая выполнение программы в режиме Шаг, найти команду, являющуюся причиной ошибки; исправить ее; выполнить

пп. 5, а — 5, в;

е) записать в IR значение аргумента х < а (в области допустимых значений); выполнить пп. 5, б и 5, в;

ж) записать в IR недопустимое значение аргумента х и выполнить пп. 5, б и 5, в.

6. Для выбранного допустимого значения аргумента х наблюдать выполне­ние отлаженной программы в режиме Шаг и записать в форме табл. 2 содержимое регистров ЭВМ перед выполнением каждой команды.

Таблица 2.Содержимое регистров

 

РС	Асс	М(30)	М(20)	РС	Асе	М(30)	М(20)

Таблица 3.Функции

 

K	Fk(x)	k	Fk(x)
	x + 17; 2≤х≤12 1-х		( x + 2)² ; 50≤x≤75
	(х + 3)2 ; 1≤x≤50 x	6.	2x² +17; 1≤x≤30 х
	1000 ; 50≤x≤15 х + 10		x² +2x; 50≤x≤50 х
4	(х + 3);³ ; 20≤x≤20		8100 ; 1≤x≤90 х²

Таблица 4.Варианты задания 1

 

Номер варианта	i	j	а	Номер варианта	i	j	а
			-20

 

Содержание отчета

Отчет о лабораторной работе должен содержать следующие разделы:

1.Формулировка варианта задания.

2. Граф-схема алгоритма решения задачи.

3. Размещение данных в ОЗУ.

4. Программа в форме табл. 1

5. Последовательность состояний регистров ЭВМ при выполнении программы в режиме Шаг для одного значения аргумента.

6. Результаты выполнения программы для нескольких значений аргумента, выбранных самостоятельно.

Контрольные вопросы

1. Что такое система команд ЭВМ?

2. Какие способы адресации использованы в модели ЭВМ? В чем отличие между ними?

3. Как просмотреть и, при необходимости, отредактировать содержимое ячейки памяти?

4. Какие способы адресации операндов применяются в командах ЭВМ?

5. Как работает механизм косвенной адресации?

6. Какая ячейка будет адресована в команде с косвенной адресацией через ячейку 043, если содержимое этой ячейки равно 102 347?

7. Как работают команды передачи управления?

8. Что входит в понятие "отладка программы"?

9. Какие способы отладки программы можно реализовать в модели?

 

 

Лабораторная работа 4

Цель работы

Изучение принципов конвейерной обработки с помощью простейшей имитационной модели.

 

 

Основные вопросы теории

Максимальная производительность современных процессоров и ЭВМ опре-

деляется, в первую очередь, уровнем развития соответствующей технологии, ко-

торая ограничивает время распространения сигнала по электронным схемам.

Дальнейшее увеличение производительности возможно за счёт архитектурных

решений. Одним из основных способов построения высокопроизводительных сис-

тем является параллелизм. Параллельная обработка реализуется двумя способами:

- во времени;

- в пространстве.

Первый способ называют конвейерным, а второй - матричным. В обоих слу

чаях необходимо использовать несколько обрабатывающих устройств, количество

которых определяет максимальное число параллельных процессов.

Известно, что типичную арифметическую команду можно разделить на сле-

дующие микрооперации:

1) выборка команд из памяти (по адресу в счётчике команд);

2) декодирование кода операции;

3) выборка операндов из регистров;

4) выполнение операции в АЛУ;

5) запоминание результата в регистре.

Если в системе имеется пять обрабатывающих устройств, каждое из которых

обеспечивает выполнение одной из перечисленных микроопераций, то имеется

возможность реализовать конвейерную обработку. Устройства должны быть спе-

циализированными. Их необходимо расположить в порядке следования микроопе-

раций в типовой команде, что позволит совместить выполнение отдельных микро-

операций разных команд и сократить общее время обработки данных.

Если предположить, что каждая микрооперация занимает один такт машин-

ного времени, то реализация последовательности из нескольких (например, трёх)

команд с совмещением может быть представлена в виде схемы, показанной на ри-

сунке 1.

 

(1) (2) (3) (4) (5)

(1) (2) (3) (4) (5)

(1) (2) (3) (4) (5)

 

Рисунок 1- Возможное совмещение микроопераций при выполнении трех

последовательных команд (в скобках указаны номера микроопераций)

 

 

Из рисунка видно, что результат первой команды будет получен после пято-

го такта, второй после шестого, а третьей после седьмого. Таким образом, среднее время выполнения последовательности из трех команд будет равно2.33такта.

С увеличением длины последовательности это время уменьшается и в пределе

стремится к одному такту. Такой эффект наблюдается только при одинаковых

длительностях микроопераций. Если эти длительности отличаются, то некоторые

устройства будут простаивать, и среднее время выполнения команды увеличится.

Для согласования работы устройств в таких условиях применяют буферизацию.

Эффективность работы произвольного конвейера определяется величиной

разности между средним временем выполнения команды в нем и предельным

временем. Целью предлагаемой лабораторной работы является исследование

влияния длины последовательности команд и соотношения длительностей отдель-

ных микроопераций на эффективность работы конвейера.

 

 

Лабораторная работа № 5

Подпрограммы и стек

Цель работы

Изучение стековой памяти

 

Пример 1

Даны три массива чисел. Требуется вычислить среднее арифметическое их максимальных элементов. Каждый массив задается двумя параметрами: адре­сом первого элемента и длиной.

Очевидно, в программе трижды необходимо выполнить поиск максимального элемента массива, поэтому следует написать соответствующую подпро­грамму.

Параметры в подпрограмму будем передавать через регистры: R1 — началь­ный адрес массива, R2 — длина массива.

Рассмотрим конкретную реализацию этой задачи. Пусть первый массив на­чинается с адреса 085 и имеет длину 14 элементов, второй— 100 и 4, тре­тий— 110 и 9. Программа будет состоять из основной части и подпрограм­мы. Основная программа задает параметры подпрограмме, вызывает ее и со­храняет результаты работы подпрограммы в рабочих ячейках. Затем осуществляет вычисление среднего арифметического и выводит результат на устройство вывода. В качестве рабочих ячеек используются регистры общего назначения R6 и R7 — для хранения максимальных элементов массивов. Подпрограмма получает параметры через регистры R1 (начальный адрес мас­сива) и R2 (длина массива). Эти регистры используются подпрограммой в качестве регистра текущего,адреса и счетчика цикла соответственно. Кроме того, RЗ используется для хранения текущего максимума, а R4 — для вре­менного хранения текущего элемента. Подпрограмма возвращает результат через аккумулятор. В табл. 1 приведен текст основной программы и под­программы. Обратите внимание, цикл в подпрограмме организован с по­мощью команды JRNZ, а модификация текущего адреса— средствами пост­инкрементной адресации.

Таблица 1.Программа примера 1

 

Команда	Примечания
Основная программа
RD #85	Загрузка
WR R1	параметров
RD #14	первого
WR R2	массива
CFLL M	Вызов подпрограммы
WR R6	Сохранение результата
RD #100	Загрузка
WR R1	параметров
RD #4	второго
WR R2	массива
CFLL М	Вызов подпрограммы
WR R7	Сохранение результата
RD #110	Загрузка
WR R1	параметров
RD #9	третьего
WR R2	массива
CALL М	Вызов подпрограммы
ADD R7	Вычисление
ADD R6	среднего
DIV #3	арифметического
ОUТ	Вывод результата
Подпрограмма МАХ
HLT	Стоп
М: RD @R1	Загрузка
WR RЗ	первого элемента в RЗ
L2: RD @R1+	Чтение элемента и модификация адреса
WR R4	Сравнение
SUB R3	и замена,
JS L1	если RЗ < R4
MOV R3,R4
LI: JRNZ R2, L2	Цикл
RD RЗ	Чтение результата в Асc
RЕТ	Возврат

Задание 1

Составить и отладить программу учебной ЭВМ для решения следующей за­дачи. Три массива в памяти заданы начальными адресами и длинами. Вычис­лить и вывести на устройство вывода среднее арифметическое параметров этих массивов.

Таблица 2.Соответствие между номерами заданий

 

Номер варианта задания

Номер строки в табл. 1

Содержание отчета

1.Формулировка варианта задания.

2. Граф-схема алгоритма основной программы.

3. Граф-схема алгоритма подпрограммы.

4. Распределение памяти (размещение в ОЗУ переменных, программы и не­обходимых констант).

5. Тексты программы и подпрограммы.

6. Зн