Цель работы: Построить логическую схему на основе высказываний путем упрощения выражен
Теоретическая часть:
Теоретической основой построения ЭВМ являются специальные математические дисциплины. Одной из них является алгебра логики, или булева алгебра (Дж. Буль — английский математик прошлого столетия, основоположник этой дисциплины). Ее аппарат широко используют для описания схем ЭВМ, их оптимизации и проектирования.
Вся информация в ЭВМ представляется в двоичной системе счисления. Поставим в соответствие входным сигналам отдельных устройств ЭВМ значения переменных хi(i = 1, n), а выходным сигналам — значения функций yj(j=1,m)(рис. 2.1).
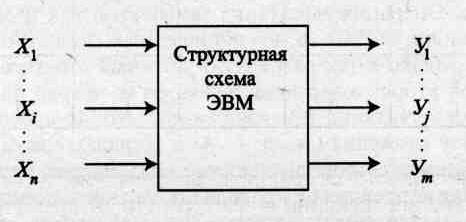
Рис. 2.1.Представление схемы ЭВМ
В этом случае зависимостями
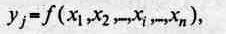
где: хi, — i-йвход;
п — число входов;
уj—j-й выход;
т — число выходов в устройстве,
можно описывать алгоритм работы любого устройства ЭВМ. Каждая такая зависимость уjявляется «булевой функцией, у которой число возможных состоянии и каждой ее независимой переменной равно двум» (стандарт ISO 2382/2-76), т.е. функцией алгебры логики, а ее аргументы определены на множестве {0,1}. Алгебра логики устанавливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простейших функций. Рассмотрим наиболее употребительные из них.
Известно, что количество всевозможных функций N от п аргументов выражается зависимостью
 (2.3)
(2.3)
При n=0 можно определить две основные функции (N=2), не зависящие от каких-либо переменных: у0, тождественно равную нулю (у0≡0), и у1тождественно равную единице (y1≡1). Технической интерпретацией функции y1≡1 может быть генератор импульсов. При отсутствии входных сигналов на выходе этого устройства всегда имеются импульсы (единицы). Функция может быть интерпретирована отключенной схемой, сигналы от которой не поступают ни к каким устройствам.
При п=1 зависимость (2.3) дает N=4. Представим зависимость значений этих функций от значения аргумента х в виде специальной таблицы истинности (табл. 2.4).
Таблица 2.4. Таблица функций от одной переменной
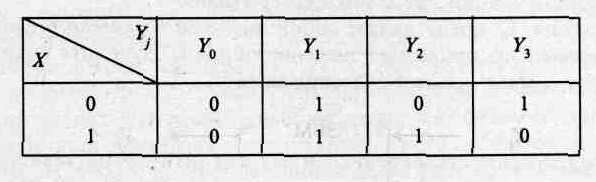
Таблицы истинности получили такое название, потому что они определяют значение функции в зависимости от комбинации входных сигналов. В этой таблице, как и ранее, у0≡0 и y1≡1. Функция у2=х, а функция у3=x (инверсия х).
Этим функциям соответствуют определенные технические аналоги. Схема, реализующая зависимость у2=х,называется повторителем, а схема у3=x— инвертором.
При п=2, N=16, т.е. от двух переменных можно построить шестнадцать различных функций. В табл. 2.5 представлена часть из них, имеющая фундаментальное значение при построении основных схем ЭВМ.
Таблица 2.5 Таблица функций от двух переменных
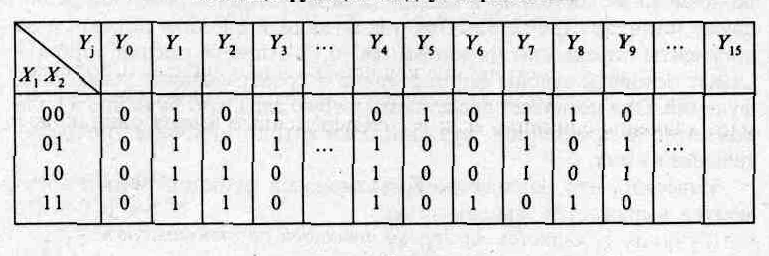
Заметим, что в левой части таблицы перечислены всевозможные комбинации входных переменных (наборы значений), а в правой — возможные реакции выходных сигналов. В табл. 2.5 представлены функции у0-у3, полностью соответствующие функциям из табл. 2.4, а также новые, часто используемые и интересные функции у4-у9. При этом местоположение функций и их нумерация в таблице особого значения не имеют. По данной таблице нетрудно составить аналитическое выражение (зависимость) для каждой функции от двух аргументов вида (2.2). Для этого наборы переменных, на которых функция принимает значение единицы, записываются как конъюнкции (логическое умножение) и связываются знаками логического сложения. Такие формы функций получили название дизъюнктивных нормальных форм (ДНФ). Если в этих функциях конъюнкции содержат все без исключения переменные в прямом или инверсном значении, то такая форма функций называется совершенной.
Функция y4 представляет собой функцию логического сложения, дизъюнкцию. Она принимает значение единицы, если хотя бы одна переменная х{или х2имеет значение единицы:
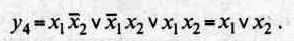
Тождественность перечисленных аналитических зависимостей можно установить, пользуясь приведенными ниже законами алгебры логики.
Функция у, является инверсной функцией по отношению к у4:
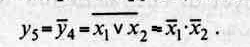
Она имеет название «отрицание дизъюнкции». Иногда в литературе встречается ее специальное название — «стрелка Пирса», по фамилии математика, исследовавшего ее свойства.
Функция у6является функцией логического умножения. Она очень похожа на операцию обычного умножения и принимает значение единицы в тех случаях, когда все ее переменные равны единице:
У6 = х1●х2.
Функция у7 является инверсной функцией по отношению к у6:
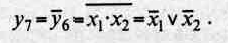
Она называется «отрицание конъюнкции» или «штрих Шеффера».
Функция y8 называется логической равнозначностью. Она принимает значение единицы, если все ее переменные имеют одинаковое значение (или 0, или 1):
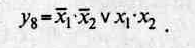
Функция у9является инверсной функцией по отношению к у8
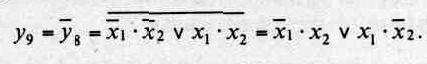
Она принимает значение единицы, если ее переменные имеют противоположные значения. Далее будет показано, что функции у8и у9являются основой для построения сумматоров, так как они соответствуют правилам формирования цифр двоичных чисел при сложении (вычитании).
Из перечисленных функций двух переменных можно строить сколь угодно сложные зависимости, отражающие алгоритмы преобразования информации, представленной в двоичной системе счисления. Алгебра логики устанавливает правила формирования логически полного базиса простейших функций, из которых могут строиться любые более сложные. Наиболее привычным базисом является набор трех функций {инверсия —「, дизъюнкция —V, конъюнкция — Λ или &}. Работа с функциями, представленными в этом базисе, очень похожа на использование операций обычной алгебры.
Алгебра логики устанавливает, что существуют и другие комбинации простейших логических функций, обладающих свойством логической полноты. Например, наборы логических функций {инверсия, дизъюнкция} и (инверсия, конъюнкция} также являются логически полными. Наиболее интересны минимальные базисы, включающие по одной операции {«отрицание дизъюнкции ()»} и {«отрицание конъюнкции ()»}- Однако работа с функциями, представленными в указанных базисах, требует от специалистов по проектированию ЭВМ определенных навыков.
Законыалгебры логики
Из определения вышеприведенных функций можноустановить целый ряд простейших свойств:
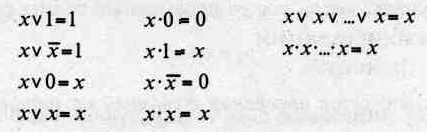
В алгебре логики установлен целый ряд законов, с помощью которых возможно преобразование логических функций (ЛФ):
• коммутативный (переместительный):

• ассоциативный (сочетательный):

Эти законы полностью идентичны законам обычной алгебры;
• дистрибутивный (распределительный):

• закон поглощения. В дизъюнктивной форме ЛФ конъюнкция меньшего ранга, т.е. с меньшим числом переменных, поглощает все конъюнкции большего ранга, если ее изображение содержится в них. Это же справедливо и для конъюнктивных форм:

• законы склеивания:
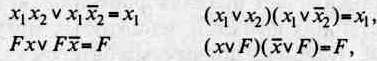
где F — логическая функция общего вида, не зависящая от переменной х;
• закон свертки:

• правило де Моргана:

Убедиться в тождественности приведенных зависимостей можно путем аналитических преобразований выражений или путем построения таблицы истинности для ЛФ, находящихся в левой и правой частях. Используя данные зависимости, можно преобразовывать исходные выражения в более простые (минимизировать их). По упрощенным выражениям можно построить техническое устройство, имеющее минимальные аппаратные затраты.
Дата: 2016-10-02, просмотров: 358.