Для побудови моделі процесу функціонування необхідно описати процеси появи та усунення відмов на формальній мові подій і станів технологічної системи, що дасть змогу визначити ймовірність знаходження технологічної системи в кожному зі станів. При такому підході можна за єдиною методикою, детально розробленою в теорії масового обслуговування, знайти коефіцієнт готовності і технічну продуктивність складних технологічних систем.
Коефіцієнт готовності
Оскільки технологічна система є об'єктом з відмовами, що усуваються в процесі його експлуатації, то у найпростішому випадку можна виділити два стани цієї системи:
працездатний стан 0, коли технологічна система функціонує і випускає продукцію, ймовірність знаходження в якому дорівнює Р0;
непрацездатний стан 1, коли технологічна система не функціонує через роботи з усунення відмови, ймовірність знаходження в якому дорівнює Р1.
Технологічна система може змінювати свій стан у будь-який момент часу. Перехід технологічної системи із одного стану в інший відбувається практично моментально, у випадкові моменти виходу з ладу технологічної системи чи завершення її відновлення. Сума ймовірностей знаходження системи в усіх зазначених n станах дорівнюватиме одиниці, тобто
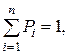
|
що дає для технологічної системи із двома можливими станами
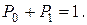
|
Перехід системи із одного стану в інший називається подією. Послідовність однорідних подій, що відбуваються одна за одною у випадкові моменти часу, створює потік випадкових подій. Оскільки можливі стани технологічної системи перелічені, а моменти можливих переходів із одного стану в інший не фіксовані і можуть настати в будь-який час, то процес функціонування являтиме собою марковський випадковий процес із дискретними станами і безперервним часом. Випадковий потік подій, який має властивості стаціонарності, ординарності, та не має післядії, буде найпростішим, або стаціонарним пуасонівськBV потоком.
Аналізуючи випадкові процеси із дискретними станами технологічної системи, використаємо для зручності граф станів, у якому стани позначаються вершинами графа, а переходи із одного стану в інший — його дугами (рис. 2.13).
Нехай система в момент часу 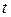 і перебувала в стані 0. Ймовірність того, що за малий проміжок часу
і перебувала в стані 0. Ймовірність того, що за малий проміжок часу 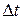 вона перейде у стан 1, позначимо
вона перейде у стан 1, позначимо 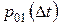 / Ця ймовірність буде ймовірністю появи відмови у функціонуванні технологічної системи, а потік випадкових подій являтиме собою потік відмов. Тоді щільність ймовірності або інтенсивність цього переходу визначиться як
/ Ця ймовірність буде ймовірністю появи відмови у функціонуванні технологічної системи, а потік випадкових подій являтиме собою потік відмов. Тоді щільність ймовірності або інтенсивність цього переходу визначиться як
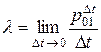 . .
|
При малих значеннях 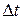 матимемо спрощене співвідношення
матимемо спрощене співвідношення
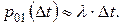
|
Беручи до уваги, що час функціонування технологічної системи може
вимірюватись у циклах, позначивши ймовірність невиконання одного циклу 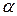 , отримаємо для ймовірності цього переходу
, отримаємо для ймовірності цього переходу
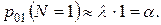
|
Якщо тривалість переходів технологічної системи із стану 0 в стан 1 розподілиться за експоненційним законом, то густина ймовірності переходу збігатиметься з параметром експоненційного закону розподілу 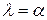 . Потік відмов вважається безперервним, оскільки функціонування технологічної системи розглядається упродовж багатьох циклів N, тобто тривалий час, порівняно з яким тривалість одного робочого циклу Т є безмежно малою величиною. У цьому випадку виконується умова
. Потік відмов вважається безперервним, оскільки функціонування технологічної системи розглядається упродовж багатьох циклів N, тобто тривалий час, порівняно з яким тривалість одного робочого циклу Т є безмежно малою величиною. У цьому випадку виконується умова
| NT>>T. |
Тоді параметр потоку відмов визначиться як
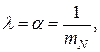
|
де 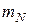 — середній час між двома відмовами, виражений кількістю робочих циклів.
— середній час між двома відмовами, виражений кількістю робочих циклів.
Ймовірність того, що за малу кількість циклів 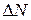 технологічна система перейде із стану 1 в стан 0, позначимо
технологічна система перейде із стану 1 в стан 0, позначимо 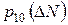 . Вона характеризує ймовірність відновлення функціонування технологічної системи, а потік випадкових подій буде потоком відновлень. Час відновлення працездатності технологічної системи є також випадковою величиною, тому інтенсивність відновлення визначиться як
. Вона характеризує ймовірність відновлення функціонування технологічної системи, а потік випадкових подій буде потоком відновлень. Час відновлення працездатності технологічної системи є також випадковою величиною, тому інтенсивність відновлення визначиться як
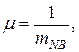
|
де 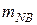 — середній час відновлення працездатності технологічної системи, виражений кількістю технологічних циклів.
— середній час відновлення працездатності технологічної системи, виражений кількістю технологічних циклів.
Щоб визначити ймовірність перебування технологічної системи в момент часу N в j-му стані, сформуємо систему диференційних рівнянь Колмогорова за формальними правилами. У лівій частині 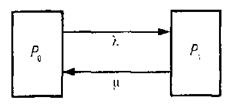 кожного рівняння записується похідна по часу, вираженому в циклах, від ймовірності знаходження технологічної системи в j-му стані в момент реалізації якогось циклу, а в правій — члени, що відповідають дугам, які з'єднують вершину даного стану з іншими. Кожен член дорівнює добуткові інтенсивності переходу (
кожного рівняння записується похідна по часу, вираженому в циклах, від ймовірності знаходження технологічної системи в j-му стані в момент реалізації якогось циклу, а в правій — члени, що відповідають дугам, які з'єднують вершину даного стану з іншими. Кожен член дорівнює добуткові інтенсивності переходу ( 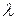 чи
чи 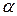 ) на ймовірність того і-го стану, із яким зв'язана дуга графа. Якщо ця дуга входить у даний стан, то знак добутку додатний, якщо виходить — то від'ємний.
) на ймовірність того і-го стану, із яким зв'язана дуга графа. Якщо ця дуга входить у даний стан, то знак добутку додатний, якщо виходить — то від'ємний.
Для технологічної системи, граф якої представлений нарис. 2.13, отримаємо
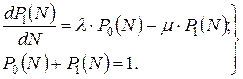
|
Якщо розглядати усталений режим довготривалого функціонування технологічної системи, тобто при 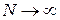 , то всі похідні можуть бути прирівняні до нуля і система диференційних рівнянь перетвориться на систему алгебраїчних:
, то всі похідні можуть бути прирівняні до нуля і система диференційних рівнянь перетвориться на систему алгебраїчних:
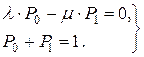
|
Ці рівняння дають змогу визначити коефіцієнт готовності технологічної системи КГ як ймовірність Р0 перебування технологічної системи в працездатному стані у будь-який момент часу при усталеному режимі функціонування:
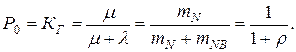
|
Дата: 2016-09-30, просмотров: 266.