Процес функціонування проходить в умовах дії багатьох факторів збурення, які час від часу призводять до невиконання технологічної або транспортної операції через відмову технологічної чи транспортної підсистем та порушення працездатності технологічної системи. Вважа­тимемо її працездатною тоді, коли в кожному циклі роботи успішно реа­лізуються технологічний та транспортний процеси, тобто на вихід без­перебійно надходять вироби заданої якості. Вирізнимо такі порушення працездатності технологічної системи:

технологічна система працює безперебійно, але якість виробу не відповідає заданим технічним вимогам;

технологічна система працює з перебоями і непередбаченими зу­пинками, але якість виробу відповідає заданим технічним вимогам.

В обох випадках порушення працездатності сталися відмови, але вони мають різні критерії визначення і різну фізичну природу. Поділи­мо відмови на технологічні, що виникають під час взаємодії інструментів із заготовкою, та транспортні, що виникають під час взаємодії транс­портного модуля з заготовкою; оскільки їх природа та наслідки різні, відмови виникають у різних типах технічних засобів, які через це мо­жуть бути досліджені окремо.

У першому випадку відбулося порушення точності параметрів ви­робу, тобто технологічна відмова — вихід параметра якості виробу за встановлені допуском межі. Такі відмови виникають при взаємодії ро­бочого модуля з заготовкою як результат випадкової несприятливої комбінації розсіяння параметрів виробу, режимів та умов експлуатації.

У другому випадку відбулася відмова у безперервності потоку заго­товок, так звана транспортна відмова. Вона виникає при взаємодії транс­портного модуля з заготовкою, наприклад, при її неподаванні або не­точному подаванні на робочу позицію.

Модель технологічної відмови може бути побудована при розгляді технічної функції, показником якості якої є параметр виробу, наприк­лад, уже розглянутий оброблюваний розміру y. Оскільки допуск на цей розмір задасться як різниця між максимально допустимим та мінімаль­но допустимим значеннями

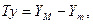
ймовірність знаходження оброблюваного розміру в межах поля допус­ку може бути визначена тільки для відомого закону розподілу його зна­чень. У більшості технологічних систем вважається, що розсіяння по­казників якості виробів описується нормальним законом розподілу. Ця гіпотеза грунтується на таких міркуваннях. У виробничих умовах об­робка деталі супроводжується впливом багатьох факторів збурення. Тоді, базуючись на центральній граничній теоремі А.М.Ляпунова, з якої вип­ливає, що коли випадкова величина у являє собою суму впливів значно­го числа взаємно незалежних випадкових величин, вплив кожної з яких є нескінченно малий, то вона розподілиться за законом, близьким до нормального. Прийнявши допущення про нормальність розподілу по­казника y, отримаємо вираз

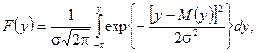
де М(у) — математичне сподівання значення показника якості виробу.

Ймовірність того, що оброблюваний розмір не вийде за межі поля допуску, визначиться за допомогою нормованої функції Лапласа Ф(і) таким чином:

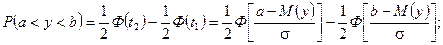
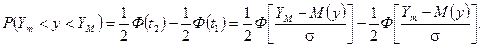
де Ф — значення нормованої функції Лапласа; σ — середнє квадратич­не розсіяння розміру у; Y_M, Y_m — найбільше і найменше допустимі зна­чення оброблюваного розміру; М(у) — математичне сподівання, або се­редина поля розсіяння значень розміру.

Тоді ймовірність виходу розміру за межі поля допуску визначиться як

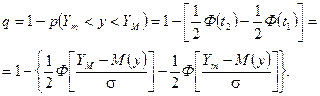
Як бачимо, ймовірність виходу показника якості виробу за задані межі q являє собою ймовірність, розраховану на одиницю часу — робочий цикл, тому може розглядатися як часова щільність імовірності викиду випадко­вої функції, що описує процес довготривалого функціонування. Якщо потік відмов буде найпростішим, то ймовірність виходу q відповідатиме інтенсивності переходу технологічної системи із працездатного стану в непрацездатний. Враховуючи, що відмови в технологічних системах ми розділили на два види — технологічні та транспортні, позначимо ймовір­ність технологічної відмови через α.

При розгляді багатоопераційних технологічних систем, у процесі функціонування яких утворюється багато параметрів виробу, кожна тех­нологічна операція розглядається як складна технічна функція, що в загальному випадку формує декілька параметрів. Нехай i-та технологічна операція створює j параметрів виробу, які опишуться вектором

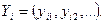
Тоді ймовірність безвідмовного виконання технологічної операції визначиться як

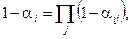
де α_ij — ймовірність нереалізації j-го параметра виробу під час вико­нання i-ї операції.

Ймовірність відмови технічних засобів, що реалізують цю техноло-
гічну операцію, визначимо при допущенні про малість значень 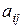виг-
ляді

.

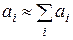Модель транспортної відмови. Транспортний процес складається із міжопераційних транспортувань заготовок від однієї робочої позиції до іншої, створюючи розгалужений потік заготовок через технологічну сис­тему. В основу побудови його моделі покладемо представлення транс­портної операції, яка описує транспортування однієї заготовки між двома сусідніми робочими позиціями, у вигляді технічної функції транспортно­го технічного засобу — транспортного модуля. Транспортна операція, своєю чергою, складається із транспортування і позиціонування заготов­ки відносно приймального елемента по прямолінійній, коловій чи складній траєкторії та спряження (з'єднання) з ним. Очевидно, що спряження — процес з'єднання деталі з приймальним елементом —

являє собою най­простішу транспортну технічну функцію, для якої просто вибрати показ­ник якості. Для реалізації спряження необхідно забезпечити точне взаєм­не положення заготовки відносно приймального елемента в площині, перпендикулярній рухові спряження. Оскільки спряження результує пе­реміщення і позиціонування заготовки, то ймовірність його реалізації визначатиме ймовірність реалізації відповідної частини транспортної операції. Тоді ймовірність успішної реалізації транспортної операції зве­деться до знаходження ймовірностей успішної реалізації усіх її спряжень.

Розглянемо поширений на практиці транспортний процес переміщен­ня заготовок типу тіл обертання між двома сусідніми робочими позиція­ми.

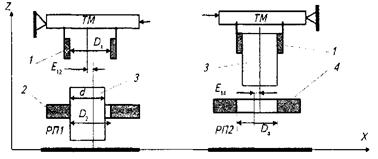
Транспортна операція виконується одиничним транспортним моду­лем (рис. 2.11), який рухається вздовж осі з'єднуючи між собою робочі позиції РП1 і РП2. Транспортний модуль захоплює заготовку З, розміщену в передавальному елементі 2 робочої позиції РП1, транспортує її до ро­бочої позиції РП2 та подає її в приймальний елемент 4.

Ймовірність відмови під час виконання цієї транспортної операції визначатиметься ймовірностями виконання спряжень заготовки із транс­портним модулем. При цьому виконуються два спряження заготовки з приймальними елементами:

· спряження СПР13 між приймально-передавальним елементом 1 транспортного модуля та заготовкою З, розміщеною на робочій позиції РП1;

· спряження СПР34 між заготовкою 3, утримуваною в приймально-передавальному елементі транспортного модуля, та приймальним еле­ментом 4 робочої позиції РП2.

Показником вихідної характеристики спряження як простої транс­портної функції виберемо вектор, який описує сукупність координат точок, в які необхідно встановити транспортовану заготовку. Тоді точність реалізації спряження транспортним модулем буде безпосередньо визначатись вектором похибок, що відображає відхилення положення дійсних точок заготовки в кінці транспортування від ідеального або за­даного положення. Умови виконання спряження залежать від взаємно­го положення перерізів заготовки і приймального елемента в площині, перпендикулярній рухові спряження.

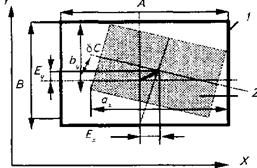Розглянемо умови реалізації спряження вздовж осі 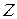для заготовки із прямокутним перерізом із приймальним елементом такого ж перерізу в площині ХОУ, перпенди­кулярній до осі 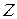. Для цьо­го необхідно виконати дві умови (рис. 2.12):

1. сумістити центр систе­ми координат заготовки 2 з центром системи коорди­нат приймального елемен­та 1;

2. зорієнтувати осі систе­ми координат заготовки па­ралельно осям системи ко­ординат приймального елемента.

Визначимо ймовірність успішної реалізації спряження як ймовірність
потрапляння координат 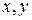центра заготовки 2 в ділянку приймального
елемента 1 у вигляді прямокутника розміром 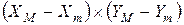в площині ХОУ, що визначається гранично допустимими зміщеннями за­готовки відносно приймального елемента при позиціонуванні. Розгля­даючи положення координат центра заготовки як випадкові величини і прийнявши допущення про їх незалежність одна від одної та нор­мальність розподілу, виразимо верхні 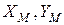і нижні 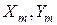допустимі значення через значення зазорів 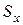та 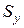у напрямах осей X та У між розмірами приймального елемента та заготовки (рис. 2.12):

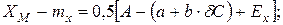
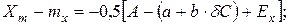
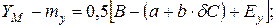
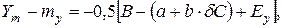
де Е_х , Е _у — похибки налагодження приймального елемента; 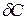— по­хибка повороту перерізу заготовки відносно перерізу приймального еле­мента.

Ймовірність успішної реалізації цього спряження є складною подією, яка включає подію успішної реалізації спряження в напрямі осі X та подію успішної реалізації спряження в напрямі осі У. Ймовірність нереалізації цього спряження 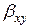визначиться за умови 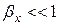та 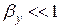, яка відповідає режимам стабільного транспортного процесу, таким чином:

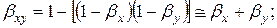
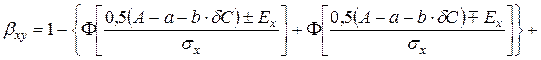
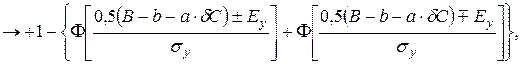
де Ф — нормована функція Лаплас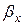а; та 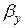— ймовірності невиконан­ня умов спряження вздовж кожної з координатних осей приймального елемента: 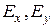— похибки налагодження приймального елемента; 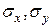— середні квадратичні розсіяння положення заготовки відносно прий­мального елемента, що визначаються дією випадкових факторів: зазо­рами в кінематичних ланцюгах, зміною характеристик сил тертя, тем­пературними коливаннями, коливаннями розмірів та форми заготовок, наявністю на заготовках задирок, деформацій та інших дефектів.

Для визначення середніх квадратичних відхилень 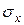та 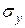положен­ня заготовки відносно приймального елемента необхідно проаналізувати точність позиціонування заготовки при багаторазовому повторенні спря­ження, тобто функціональну точність транспортної підсистеми. Ця точність залежить від складності траєкторії позиціонування, яка визна­чається кількістю окремих переміщень заготовки, та величини і швид­кості цих переміщень.