Розглянемо найпростішу автоматичну технологічну систему, яка реалізує одну технологічну операцію із показником якості — параметр виробу, наприклад, оброблюваний розмір. Вплив факторів збурення призведе до того, що при довготривалому функціонуванні час від часу на виході технологічної системи з'являтимуться браковані вироби, тоб­то вироби, оброблюваний розмір яких вийшов за межі поля допуску. Браковані вироби можуть з'являтися з різних причин, конкретний вплив яких невідомий. Це характерний приклад дії факторів збурення, коли їх вплив на функціонування технологічної системи не залишається пос­тійним. А це значить, що кількість виробів, виготовлених між двома бракованими, буде випадковою величиною, яка розподіляється за пев­ним законом. Коливання кількості доброякісних виробів між двома по­слідовними бракованими виникає в цьому випадку не за рахунок коли­вань властивостей різних екземплярів технологічної системи, а внаслі­док зміни умов їх роботи. Як бачимо, коливанням властивостей техніч­них засобів можна знехтувати стосовно коливань умов їх роботи. Влас­тивість технологічної системи зберігати під час довготривалого функціо­нування здатність до випуску доброякісних виробів визначається як її надійність. Знайдемо на основі даних про функціональну точність та­кий показник надійності, як безвідмовність технологічної системи.

Нехай працездатність технологічної системи із технічним засобом для реалізації однієї технологічної операції визначається отриманим показником (розміром) y. Створення розміру у і буде функцією цієї тех­нологічної системи, точніше, її технічного засобу, який далі називати­мемо робочим модулем. Здатність робочого модуля до довготривалого відтворення розміру у із заданою точністю визначить його надійність. Точність реалізації розміру задається верхнім Y_M та нижнім Y_m гранич­ними відхиленнями, які визначають допуск Ту.

Робочий модуль вважається працездатним в інтервалі (0, t), якщо значення реалізованого показника у* не перетинає верхню Y_M чи ниж­ню Y_m межі (рис.2.10). Відсутність перетину означає виконання нерів­ності

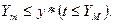
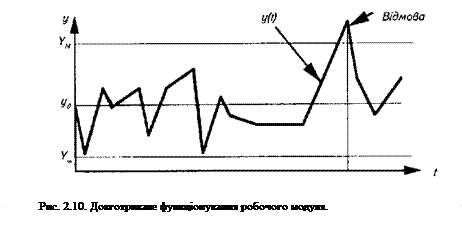
Вважатимемо, що за час t робочий модуль обробив N виробів. На обробку одного виробу витрачається час тривалості циклу Т, тому час безвідмовної роботи робочого модуля становить: 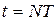. Однак для умов дискретного виробництва доцільніше відраховувати час безвідмовної роботи в кількості циклів або виготовлених виробів N. За момент настання відмови робочого модуля приймається момент перетину N-ною реалізацією обробки верхньої межі Y_M знизу вверх чи момент перетину нижньої межі Y_m зверху вниз.

Для визначення ймовірності безвідмовної роботи технологічної си­стеми упродовж заданої кількості циклів приймемо такі допущення:

1. Вихід показника технологічної операції у за задані межі — подія випадкова.

2. Ймовірність виходу показника у за задані межі при наступних реалізаціях не залежить від ймовірності виходу на попередніх, тобто в потоці реалізацій відсутня післядія.

3. Ймовірність неякісного виконання технологічної операції оброб­ки значно менша від одиниці, тобто розглядається відлагоджений про­цес функціонування технологічної системи.

Тоді ймовірність успішної обробки N виробів поспіль матиме такий вигляд:

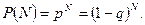
Якщо розглянути тривалий період функціонування робочого моду­ля такий, що виконується умова 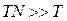, то ймовірність успішної об­робки малого числа виробів dN визначиться як

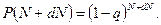
Ймовірність dР успішної реалізації малого числа циклів dN знайде­мо за формулою

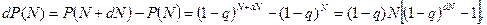
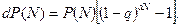
Враховуючи допущення 3, за яким величина q є малою при стабіль­ному функціонуванні технологічної системи та відлагодженому техно­логічному процесі, спростимо вираз у квадратних дужках:

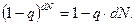
Отримаємо

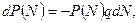
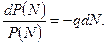
Проінтегруємо одержаний вираз, враховуючи, що на початку функ­ціонування робочий модуль справний, тобто при 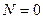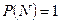, та приймемо 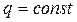, тобто умови обробки деталей не змінюються. Тоді ймовірність безвідмовної роботи робочого модуля за N робочих циклів визначиться як

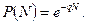
Як бачимо, ймовірність безвідмовної роботи робочого модуля опи­сується законом розподілу, параметром якого є випадкова величина. Цей параметр визначається як ймовірність виходу за задані допуском межі показника якості технічної функції, в нашому прикладі — обробленого розміру у.

Отримана модель для визначення ймовірного часу безвідмовної ро­боти робочого модуля цікава тим, що зв'язує характеристики функціо­нальної точності технологічної системи із характеристиками її надій­ності. Очевидно, що при зростанні складності технологічних процесів і відповідного ускладнення технічних засобів їх реалізації така модель стає надзвичайно зручною для опису і прогнозування надійності техно­логічної системи.