Задача типа 1. Определить гидравлический уклон i, если заданы величины расхода Q, нормальной глубины h , ширины канала по дну b, коэффициента шероховатости п и заложения откоса m?,
Задача решается прямой подстановкой в формулу Шези, записываемую в виде -
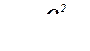 , (7.13)
, (7.13)
где w - площадь живого сечения вычисляется но формуле (7.10), м2;
c- смоченный периметр вычисляется по формуле (7.11), м;
R - гидравлический радиус, м ;
С- коэффициент Шезиу м0,5 /с.
Задача типа 2. Определить расход воды в канале Q, если заданы величины гидравлического уклона i , нормальной глубины hь ширины канала по дну b, коэффициента шероховатоcnи п и заложения откоса т.
Задача решается аналогично предыдущей е помощью формулы Шези, записанной в виде
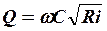 , (7.14)
, (7.14)
Задача типа 3. Определить ширину канала по дну b, если заданы величины гидравлического уклона i , расхода воды в канале Q, нормальной глубины h, коэффициента шероховатости п и коэффициента откоса т. Задача решается методом подбора - графически или аналитически с помощью ПЭВМ. Задавая ряд значений b, определяют, как и в задаче 2, расход для каждого задаваемого b и строят график зависимости Q = Q ( b ), a затем по заданному значению Q зад определяют искомую ширину канала b иск (рис7.3,а).
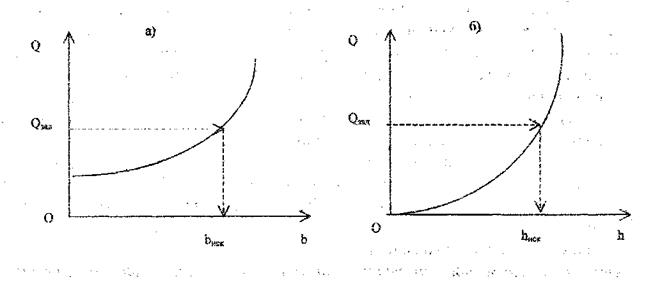
Рис. 7.3. Графическое решение задач 3 и 4 типов
Задача типа 4. Определить нормальную глубину h, если заданы величины
гидравлического уклона i, расхода воды в канале Q, ширины канала но дну b,
коэффициента шероховатости п и коэффициента откоса т.
Задача решается аналогично предыдущей, т.е. задавая ряд значений h,
определяют расход для каждой задаваемой глубины и строят график
зависимости Q = Q ( h ), а затем по заданному значению Q зад определяют
искомую глубину h иск (рис.7.3,б).
Задача типа 5. Определить нормальную глубину h и ширину канала по дну
b, если заданы величины гидравлического уклона i, расхода воды в канале Q ,
гидравлически наивыгоднейшей относительной ширины канала по дну
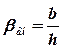 , коэффициента шероховатости п и коэффициента откоса т.
, коэффициента шероховатости п и коэффициента откоса т.
Задача решается в такой последовательности.
Задавая ряд значений h, находят соответствующие b = b гн h, а затем строят график зависимости Q = Q ( h ) и по заданному расходу Q зад определяют искомые h и b .
Примеры решения задач
Задача 7.2.1. Определить расход при равномерном движении воды в трапецеидальном канале, проложенном в суглинках, если ширина его по дну
b =5,5 м, глубина h =1,8 м, коэффициент откоса m =1 и уклон дна I =0,0004. Решение . Расход воды Q вычислим но формуле (7.14), предварительно определив среднюю скорость течения в канале но формуле
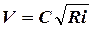
Площадь живого сечения находим по формуле (7.10)
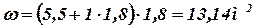
Смоченный периметр - по формуле (7.11)
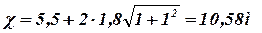
Гидравлический радиус
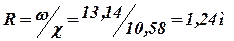
Определяем коэффициент Шези С но формуле Маннинга (7.4).
Коэффициент шероховатости берем из приложения 11 - п= 0,025.
Тогда
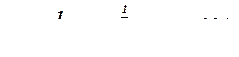
Скорость течения в канале
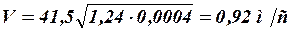
Сравним полученную скорость с максимальной неразмывающей скоростью и наименьшей незаиляющей скоростью. Первая для каналов в средних суглинках равна V неразм=1,0м/с. Вторая может быть определена по справочным таблицам в зависимости от d ср и h. В данном случае она равна
V неразм =0,57 м/с.
Так как 0,5 7м/с<0,92м/с< 1,0м/с, то капал считается устойчивым к размыву и не подвергается заилению.
Расход воды в канале при заданных условиях составит
Q = w V=13,14× 0 ,92 = 12,1 м3/с.
Задача 7.2.2. При каком наполнении h бетонный канал трапецеидального сечения пропустит расход Q=38 м3/с, если ширина его b=25 м, коэффициент откоса m=0,5 уклон дна i=0,00025?
Решение. Задачу решаем подбором. Определяем модуль расхода для заданного Q из формулы (7.5)

Задаваясь различными глубинами, вычисляем соответствующие им модули расхода по формуле
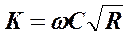
Результаты расчетов сводим в таблицу 7.1,
Таблица 7.1
| h, м | w,м | c,м | R,m | С, м0,5/с | К, м3/с |
| 2,9 2 1 | 77,75 52 25,5 | 31,5 29,48 27,24 | 2,44 1,77 0,935 | 81,2 77,7 70,5 | 9725 5350 1738 |
| 1,2 | 30,7 | 27,7 | 1,11 | 72,37 | 2340 |
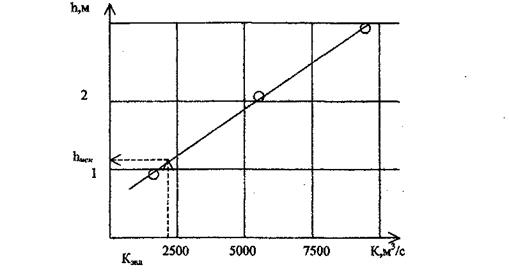
| Рис. 7.4. График K=f(h) (к задаче 7.2.2) |
Вычертив по данным таблицы 7.1 график K - f ( h ) (рис.7.4), находим, что модуль расхода K=2420 м3/с соответствует глубине h = 1,2 м.
Задача 7.2 . 3. Определить размеры земляного канала гидравлически наивыгоднейшего сечения, который при уклоне i=0,001 будет пропускать расход Q = 4 м3/с. Канал имеет трапецеидальную форму сечения с заложением откосов т =2.
Решение. Решаем задачу методом подбора. Определяем модуль заданного расхода из формулы (7.5)
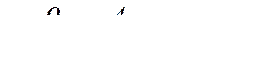
Задаваясь различными глубинами, вычисляем соответствующие им модули расхода. При этом ширину канала по дну b определяем по формуле
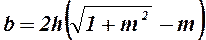
При h=l м имеем
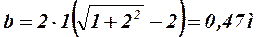 ;
;
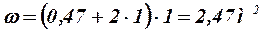

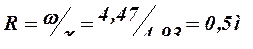
Коэффициент шероховатости для земляного канала принимаем согласно приложению 11 равным n = 0,025. При этом коэффициент Шези
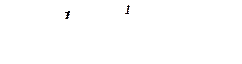
Модуль расхода
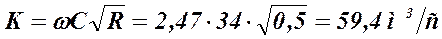
Аналогично вычисляем модули расхода для других значений глубин. Полученные данные сводим в таблицу 7.2.
Таблица 7.2
| h, м | b,м | w,м2 | c,м | R,m | С, м0,5/с | К, м3/с |
| 1,0 1,2 1,5 | 0,47 0,574 0,705 | 2,47 3,57 5,57 | 4,93 5,939 7,4 | 0,5 0,598 0,75 | 34 35,55 37,5 | 59,4 97,7 181 |
| 1,32 | 0,72 | 4,32 | 7,53 | 0,758 | 37,35 | 127,8 |
Вычертив по этим данным график K = f ( h ) (рис.7.5), находим, что модуль заданного расхода K = 127,5 м3/с соответствует глубине h=1,32 м. Проверочное вычисление показало, что модуль расхода, соответствующий глубине h=1,32 м, практически равен модулю заданного расхода.
На основании этого принимаем размеры канала: b=0,72 м; h=1,32 м.
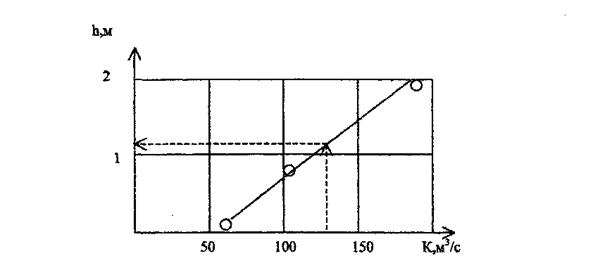
Рис. 7.5, К задаче 7.2.3.
Задача 7.2.4. Определить скорость движения воды V и расход Q в керамической трубе диаметром d=300 мм при степени наполнения a = h / d=0,7 и уклоне дна i = 0,008.
Решение. Живое сечение потока имеет вид, представленный на рисунке 7.6.
 Площадь живого сечения
Площадь живого сечения
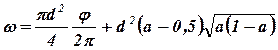
sin a=a/0,5-1=0,7/0,5-1=0,2;
a=0,201 рад; j = p+2-0,201=3,54 рад;
Рис.7.6. Живое сечение потока
(к задаче 7.2.4)
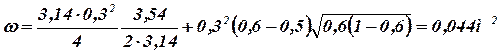
Смоченный периметр

Гидравлический радиус
R = w/c=0,044/0,53=0,083 м.
Для керамических труб коэффициент шероховатости п=0,013 (см. приложение 11).
Коэффициент Шези;
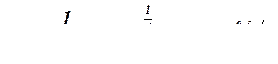
Скорость движения воды

Расход воды, протекающей по трубе,
Q = w • V = 0,044 × 1,36 = 0,0598м3
7.3. Задачи для самостоятельного решения
Задача 7.3.1. Определить среднюю скорость течения V и расход Q воды в канале трапецеидального сечения. Ширина канала по дну b = ___м, коэффициент откосов т = ___ , глубина наполнения h = ___ м, уклон дна i =____ . Стенки канала гладкие, земляные; движение - равномерное. Данные приведены в табл. 7.3.1..
Таблица 7.3.1.
| № варианта | b, м | h, м | m | i |
| 1 | 3 | 1 | 1,5 | 0,002 |
| 2 | 3,4 | 1,66 | 1,75 | 0,0018 |
| 3 | 3,9 | 1,34 | 2 | 0,0024 |
| 4 | 4 | 2 | 1,5 | 0,002 |
| 5 | 5 | 2 | 1,75 | 0,0018 |
| 6 | 5,6 | 3,5 | 2 | 0,0015 |
Задача 7 . 3.2. Определить расход воды Q B в бетонированном канале полукруглого сечения R =1 м, если падение дна на 1 км составляет 8см. Найти также расход нефти QH по тому же каналу, если плотность нефти r =880кг/м3 , а кинематический коэффициент вязкости n = 0,3 × 1 0-4 м2/с.
Задача 7 . 3 . 3. Кювет, стенки которого бетонированы, имеет в сечении форму треугольника с углом при вершине a = __° и высотой h = ___ м, должен пропускать расход Q =____ ji / c воды, не переполняясь. Определить уклон дна I .
Данные приведены в табл. 7.3.2..
Таблица 7.3.2.
| № варианта | a, ° | h, м | Q ,л/с |
| 1 | 90 | 1 | 200 |
| 2 | 80 | 1,66 | 250 |
| 3 | 100 | 1,34 | 230 |
| 4 | 120 | 2 | 340 |
| 5 | 80 | 2 | 320 |
| 6 | 95 | 3,5 | 500 |
Задача 7 . 3.4. Канал с хорошей бутовой облицовкой трапецеидального профиля (b =__ м, Н=__м, a =___°). При низкой воде глубина наполнения h = 0,5 м, а при высокой воде канал наполняется до краев. В каком отношении находятся расходы при высокой и низкой воде? Данные приведены в табл. 7.3.3..
Таблица 7.3.3.
| № варианта | b, м | H, м | a |
| 1 | 3 | 1 | 45 |
| 2 | 4 | 2 | 60 |
| 3 | 5 | 3 | 70 |
| 4 | 4 | 4 | 30 |
| 5 | 5 | 2 | 40 |
| 6 | 6 | 4 | 45 |
Задача 7 . 3.5. Какую ширину b должен иметь канал прямоугольного сечения длиной l = _____ м, вырытый в естественном грунте на глубину Н= __ 3 м, если для пропуска воды в количестве Q =___ м3/с используется естественная разность отметок его концов D z = ___ м. Данные приведены в табл. 7.3.4..
Таблица 7.3.4.
| № варианта | l, м | H, м | Q,м 3 /с | D Z , м |
| 1 | 1100 | 3 | 600 | 5 |
| 2 | 1000 | 2,5 | 600 | 4,5 |
| 3 | 2100 | 3 | 700 | 6 |
| 4 | 1900 | 4 | 300 | 6 |
| 5 | 1000 | 2 | 400 | 5 |
| 6 | 900 | 4 | 450 | 4,5 |
Задача 7 . 3.6. Бетонированный канал-лоток, имеет форму прямоугольника с основанием b = __м. Уклон дна канала составляет 1:10000. Какую глубину h , должен иметь канал, чтобы при расходе Q =____ м3/с он не переполнялся. Данные приведены в табл. 7.3.5..
Таблица 7.3.5.
| № варианта | b, м | Q,м 3 /с |
| 1 | 1,1 | 0,600 |
| 2 | 1 | 0,600 |
| 3 | 2,1 | 0,700 |
| 4 | 1,9 | 0,300 |
| 5 | 1 | 0,400 |
| 6 | 0,9 | 0,450 |
Задача7 . 3.7.Рассчитать трапецеидальный канал гидравлически наивыгоднейшего очертания и определить уклон его дна i, необходимый для пропуска расхода Q =__ м3/с при средней скорости V =__ м/с. Стенки и дно канала выложены крупным камнем; коэффициент откоса m = __. Данные приведены в табл. 7.3.6..
Таблица 7.3.6.
| № варианта | Q,м 3 /с | V, м/c | m |
| 1 | 10 | 0,7 | 1,5 |
| 2 | 15 | 0,75 | 1,75 |
| 3 | 29 | 0,7 | 2 |
| 4 | 12 | 0,75 | 1,5 |
| 5 | 16 | 0,7 | 1,75 |
| 6 | 18 | 0,75 | 2 |
Задача7 . 3.8. Определить ширину трапецеидального канала по дну b, имеющего коэффициент откоса т=__ при глубине h =__ м и уклоне дна
i =__, если в канале имеет место равномерное движение и расход воды Q =___ м3/с. Стенки канала—плотная глина. Данные приведены в табл. 7.3.7..
Таблица 7.3.7.
| № варианта | Q,м 3 /с | h, м | m | i |
| 1 | 10 | 1,7 | 2,5 | 0,00004 |
| 2 | 15 | 1,75 | 2,75 | 0,00005 |
| 3 | 29 | 1,25 | 2 | 0,00006 |
| 4 | 12 | 1,0 | 2,5 | 0,00004 |
| 5 | 16 | 1,7 | 2,75 | 0,00005 |
| 6 | 18 | 1,25 | 2,25 | 0,00006 |
Задача 7 . 3.9. Определить гидравлически наивыгоднейшие размеры канала трапецеидального сечения для пропуска воды в количестве Q =___м3 / c уклон дна канала i =___ , коэффициент откоса т=__; стенки канала земляные. Данные приведены в табл. 7.3.8..
Таблица 7.3.8.
| № варианта | Q,м 3 /с | m | i |
| 1 | 10 | 2,5 | 0,0004 |
| 2 | 15 | 2,75 | 0,0005 |
| 3 | 29 | 2 | 0,0006 |
| 4 | 12 | 2,5 | 0,0004 |
| 5 | 16 | 2,75 | 0,0005 |
| 6 | 18 | 2,25 | 0,0006 |
Задача 7 . 3.10. Рассчитать заложение откоса стенок гидравлически наивыгоднейшего канала трапецеидальной формы для пропуска расхода воды Q =__м3/с при глубине наполнения канала h = __ м и уклоне его дна i = ____; стенки канала бетонные. Данные приведены в табл. 7.3.9..
Таблица 7.3.9.
| № варианта | Q,м 3 /с | h, м | i |
| 1 | 10 | 1,7 | 0,00004 |
| 2 | 15 | 1,75 | 0,00005 |
| 3 | 29 | 1,25 | 0,00006 |
| 4 | 12 | 1,0 | 0,00004 |
| 5 | 16 | 1,7 | 0,00005 |
| 6 | 18 | 1,25 | 0,00006 |
Задача 7 . 3.11. Определить ширину канала по дну b и ширину по урезу В для условий предыдущей задачи при m =1,5.
Задача 7.3.12. В канале прямоугольного сечения шириной b =8 м течет поток воды. Глубина потока в рассматриваемом сечении h =3м. Стенки канала -бетонные, грубые. Расход воды Q =20,2 m 3 / c .Определить характер течения жидкости, если уклон дна канала i = 0,0001. Данные приведены в табл. 7.3.10..
Таблица 7.3.10.
| № варианта | Q,м 3 /с | h, м | b , м | i |
| 1 | 20 | 2,7 | 10 | 0,0004 |
| 2 | 25 | 2,75 | 8 | 0,0005 |
| 3 | 29 | 2,25 | 9 | 0,0006 |
| 4 | 22 | 3,0 | 14 | 0,0004 |
| 5 | 26 | 2,7 | 12 | 0,0005 |
| 6 | 28 | 2,25 | 12 | 0,0006 |
Задача 7.3.13. Проектируется канал наивыгоднейшего трапецеидального сечения, предназначенный для пропуска воды в количестве Q = ____ м3/с, которая забирается из реки. Вместе с ней в канал попадают и донные наносы крупностью до d =__ мм. Выбрать скорость V, при которой канал не заиляется и не размывается, если грунт, в котором он прорыт, представляет собой глину. Определить также наивыгоднейшие размеры канала и его уклон i , если коэффициент откосов т =___ и коэффициент шероховатости стенок и дна п =___. Данные приведены в табл. 7.3.11..
Таблица 7.3.11.
| № варианта | Q,м 3 /с | d, мм | m | n |
| 1 | 20 | 2,7 | 1,5 | 0,025 |
| 2 | 25 | 2,75 | 1,75 | 0,02 |
| 3 | 29 | 2,25 | 2,5 | 0,025 |
| 4 | 22 | 3,0 | 2,25 | 0,02 |
| 5 | 26 | 2,7 | 2 | 0,02 |
| 6 | 28 | 2,25 | 2 | 0,025 |
Приложения
Приложение 1
Значения кинематического коэффициента вязкости v воды в зависимости от температуры
| t,°C | vxlO6 | t,°C | vxlO6 | t,°C | vxlO6 | t,°C | vxlO6 | |
| 1 | 1.73 | 9 | 1.35 | 17 | 1.09 | 30 | 0.80 | |
| 2 | 1.67 | 10 | 1.31 | 18 | 1.06 | 35 | 0.73 | |
| 3 | 1.62 | 11 | 1.27 | 19 | 1.04 | 40 | 0.66 | |
| 4 | 1.57 | 12 | 1.24 | 20 | 1.01 | 45 | 0.60 | |
| 5 | 1.52 | 13 | 1.21 | 22 | 0.99 | 50 | 0.56 | |
| 6 | 1.47 | 14 | 1.18 | 24 | 0.92 | 55 | 0.51 | |
| 7 | 1.43 | 15 | 1.15 | 26 | 0.88 | 60 | 0.48 | |
| 8 | 1.39 | 16 | 1.12 | 28 | 0.84 | 70 | 0.41 |
Приложение 2
Объемный вес g, плотность r и коэффициент кинематической вязкости n некоторых жидкостей при температуре 20°С
| r, кг/м3 | n, см2 /c | |||||
| Наименование жидкости | ||||||
| 20°С | 50°С | 20°С | 40°С | 60°С | 80°С | |
| Анилин | 1040 | 0,043 | ||||
| Бензин | 880 | 0,0073 | 0,0059 | 0,0049 | ||
| Вода пресная | 998,2 | 0,01012 | 0,0065 | 0,0047 | 0,0036 | |
| Глицерин безводный | 1250 | 9,7 | 3,3 | 0,88 | 0,38 | |
| Керосин | 800 | 0,025 | 0,018 | 0,012 | 0,010 | |
| Масло: | ||||||
| касторовое | 960 | 15 | 3,5 | 0,88 | 0,35 | |
| трансформаторное | 884 | 880 | 0,28 | одз | 0,076 | 0,084 |
| АМГ-10 | 850 | 0,17 | 0,11 | 0,085 | 0,065 | |
| веретенное АУ | 892 | 0,48 | 0,19 | 0,098 | 0,059 | |
| индустриальное 12 | 883 | 0,48 | ОД 9 | 0,098 | 0,059 | |
| индустриальное 20 | 891 | 0,85 | 0,33 | 0Д4 | 0,080 | |
| индустриальное 30 | 901 | 1,8 | 0,56 | 0,21 | 0Д1 | |
| индустриальное 50 | 910 | 5,3 | и | 0,38 | 0Д6 | |
| турбинное | 900 | 0,97 | 0,38 | 0,16 | 0,088 | |
| Ртуть | 13547 | 0,0016 | 0,0014 | 0,0010 | ||
| Спирт этиловый | 789 | 0,00151 | ||||
| Эфир этиловый | 715 | 0,00363 | ||||
Указание. Плотность жидкости при другой температуре можно определить по формуле 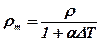
где rm - плотность жидкости при температуре Т = Т0 + DT; DT - изменение температуры: Т0 -температура, при которой плотность жидкости равна р ; a - коэффициент температурного расширения жидкости ( например, для минеральных масел в среднем можно принять a=0,00071/°С).
Приложение 3
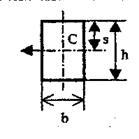
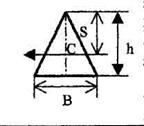
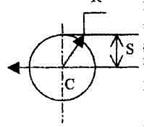
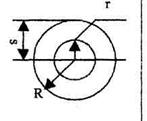
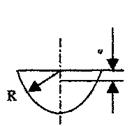
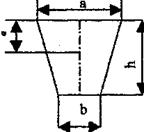
Момент инерции Jc плоских фигур относительно горизонтальной оси,
проходящей через центр тяжести; координата центра тяжести s ; площадь w .
| Фигура | Jc | s | w |
| 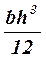
| 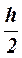
| 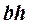
|
| 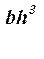
| 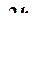
| 
|
| 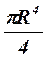
| 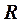
| 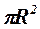
|
| 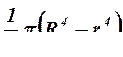
| 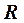
| 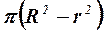
|
| 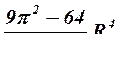
| 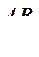
| 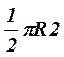
|
| 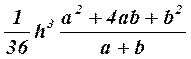
| 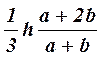
| 
|
Приложение 4
Значения эквивалентной шероховатости для труб из различных материалов
| Трубы, их материал и состояние | Dэкв ,мм |
| Цельнотянутые трубы: | |
| Новые технические гладкие из стекла, латуни, меди, | |
| свинца | 0,0015...0,01 |
| То же, из алюминия | 0,015...0,06 |
| Стальные новые | 0,02...0,05 |
| Стальные после нескольких лет эксплуатации, | |
| очищенные и бигумизированные | 0,15...0,3 |
| Стальные сварные трубы: | |
| Новые | 0,04...0,1 |
| Бывшие в эксплуатации | 0,1...0,15 |
| Умеренно заржавленные | 0,3...0,7 |
| Старые заржавленные | 0,8.. .1,5 |
| Сильно заржавленные с большими отклонениями | 2...4 |
| Оцинкованные стальные трубы: | |
| Новые чистые | 0,07...0,15 |
| Бывшие в эксплуатации | 0,18 |
| Чугунные трубы: | |
| Новые | 0,25..1 |
| Новые бигумизированные | 0,15 |
| Асфальтированные | 0,12...0,3 |
| Бывшие в эксплуатации | 1...1,5 |
| Со значительными отложениями | 2...4 |
| Очищенные, после многих лет эксплуатации | 0,3...1,5 |
| Бетонные и другие трубы: | |
| Бетонные, хорошая поверхность с затиркой | 0,3...0,8 |
| То же, при среднем качестве работ; железобетонные | 2,5 |
| То же, при грубой поверхности | 3...9 |
| Асбестоцементные новые | 0,05...0,1 |
| То же, бывшие в эксплуатации | 0,6 |
| Рукава и шланги резиновые | 0,03 |
|
Приложение 6
Значения коэффициентов zм некоторых местных сопротивлений в квадратичной области сопротивления
 Тип сопротивления Тип сопротивления
| Схема сопротивления | Значения коэффициента zм | |||||||||||
| Вход в трубу |
| 0,5 | |||||||||||
| Внезапное сужение |
|
| |||||||||||
| Внезапное расширение |
|
| |||||||||||
|
Плавный поворот |
| d/R |
| ||||||||||
| 0,2 | 0,14 | ||||||||||||
| 0,4 | 0,21 | ||||||||||||
| 0,6 | 0,44 | ||||||||||||
| 0,8 | 0,98 | ||||||||||||
| Крутой поворот |
| a° |
| ||||||||||
| 20 | 0,12 | ||||||||||||
| 30 | 0,16 | ||||||||||||
| 60 | 0,56 | ||||||||||||
| 90 | 1,19 | ||||||||||||
| Выход из трубы в резервуар |
| 1,0 | |||||||||||
| Задвижка (zзадв..) |
| a/d | Простая | Лудло | |||||||||
| 0,1 | 160 | 200 | |||||||||||
| 0,2 | 35 | 33 | |||||||||||
| 0,3 | 10 | 11 | |||||||||||
| 0,4 | 4,6 | 4,7 | |||||||||||
| 0,5 | 2,1 | 2,35 | |||||||||||
| 0,6 | 0,98 | 1,23 | |||||||||||
| 0,7 | 0,44 | 0,67 | |||||||||||
| 0,8 | 0,17 | 0,31 | |||||||||||
| 0,9 | 0,06 | 0,11 | |||||||||||
| 1 | 0,05 | 0,05 | |||||||||||
| Кран пробковый (zп.к.) |
| a° |
| ||||||||||
| 10 | 0,31 | ||||||||||||
| 20 | 1,84 | ||||||||||||
| 30 | 6,15 | ||||||||||||
| 40 | 20,7 | ||||||||||||
| 50 | 95,3 | ||||||||||||
| Тип клапана | Схема сопротивления | Значения коэффициента zм | |||||||||||
|
|
| Диаметр d, мм | |||||||||||
| 40 | 70 | 100 | 200 | 300 | 500 | 750 | |||||||
| 1,3 | 1,4 | 1,5 | 1,9 | 2,1 | 2,5 | 0,9 | |||||||
| Всасывающий клапан с сеткой (zк.с) | 12 | 8,5 | 7,0 | 4,7 | 3,7 | 2,5 | 1,6 | ||||||
| Вентиль (zв) |
| h/d | |||||||||||
| 0,2 | 0,3 | 0,5 | 0,6 | 0,7 | 0,8 | 1 | |||||||
| 13 | 5,8 | 2,0 | 1,4 | 1,0 | 0,8 | 0,5 | |||||||
Приложение 7
Значения расходных характеристик (модулей расхода) К для стальных и
____________ чугунных труб при квадратичной области сопротивления_____
| Внутренний | Площадь | Нормальные | Новые чугунные | Новые стальные | ||
| стандартный | поперечного | (бывшие в | трубы | трубы | ||
| диаметр трубы d,м | сечения трубы w, м2 | эксплуатации) трубы (стальные и чугунные) К, м3/с | К, м3/с | К, м3/с | ||
| 0,050 | 0,00196 | 8,313*10-3 | 9,947*10-3 | 10,1*10-3 | ||
| 0,075 | 0,00442 | 0,02477 | 0,02927 | 0,02970 | ||
| 0.100 | 0,00785 | 0,05361 | 0,06285 | 0,06373 | ||
| 0,125 | 0,01227 | 0,09739 | 0,11350 | 0,1151 | ||
| 0,150 | 0,01766 | 0,1584 | 0,18390 | 0,1863 | ||
| 0,200 | 0.03142 | 0,3408 | 0,3930 | 0,3980 | ||
| 0,250 | 0,04906 | 0,6164 | 0,7076 | 0,7163 | ||
| 0,300 | 0,07065 | 0,9993 | 1,1430 | 1,157 | ||
| 0,350 | 0,09616 | 1,503 | 1,715 | 1,735 | ||
| 0,400 | 0,1256 | 2,140 | 2,435 | 2,463 | ||
| 0,450 | 0,15896 | 2,920 | 3,316 | 3,354 | ||
| 0,500 | 0,19625 | 3,857 | 4,374 | 4,423 | ||
| 0,600 | 0,28260 | 6,239 | 7,053 | 7,131 | ||
| 0,700 | 0,38465 | 9,362 | 10,560 | 10,674 | ||
| 0,800 | 0,50240 | 13,301 | 14,973 | 15,132 | ||
| 0,900 | 0,63585 | 18,129 | 20,373 | 20,587 | ||
| 1.000 | 0,78500 | 23,911 | 26,832 | 27,111 | ||
| 1,10 | 0,94985 | 30,709 | 34,416 | 34.769 | ||
| 1,20 | 1,1304 | 38,601 | 43,211 | 43,650 | ||
| 1,30 | 1,32665 | 47,604 | 53,232 | 53,769 | ||
| 1,40 | 1,53860 | 57,807 | 64,581 | 65,226 |
Приложение 8
Значения поправочного коэффициента Q 1
| Вид труб | Средняя скорость потока v, м/с | ||||||||||||
| 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,5 | 3,0 | |
| Нормальные стальные и | |||||||||||||
| чугунные | 0,92 | 0,94 | 0,95 | 0,96 | 0,97 | 0,98 | 0,99 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1.00 |
| Новые чугунные | 0,81 | 0,84 | 0,86 | 0,87 | 0,89 | 0,91 | 0,92 | 0,93 | 0,94 | 0,95 | 0,96 | 0,98 | 0,99 |
| Новые стальные | 0,91 | 0,92 | 0,93 | 0,94 | 0,95 | 0,95 | 0,96 | 0,97 | 0,97 | 0,98 | 0,98 | 0,99 | 0,99 |
Приложение 9
Значение предельных средних скоростей V пред , м/с
| Трубы | Внутренние диаметры труб d, м | ||||||||
| 0,05 | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 1,0 | 1,4 | |
| Новые | 2,8 | 3,2 | 3,5 | 3,7 | 3,8 | 3,9 | 4,0 | 4,2 | 4,4 |
| стальные | |||||||||
| Новые | 2,5 | 2,8 | 3,1 | 3,3 | 3,4 | 3,5 | 3,6 | 3,8 | 4,0 |
| чугунные | |||||||||
| Нормальные | 0,8 | 0,9 | 1,0 | 1,1 | 1,1 | 1,2 | 1,2 | 1,3 | 1,3 |
| (стальные и | |||||||||
| чугунные) | |||||||||
Приложение 10
Значения стандартных диаметров d труб для пропуска рекомендуемых
предельных ( из экономических соображений) расходов воды Q
| Внутренний стандартный диаметр d, м | 0,050 | 0,075 | 0,100 | 0,125 | 0,150 | 0,200 | 0,250 | 0,300 | 0,350 | 0,400 | 0,450 | 0,500 | 0,600 | 0,700 | 0,800 | 0,900 | 1,000 | 1,100 | ||||
| Рекомендуе- мой предельный расход Q, м3/с | 0,0015 | 0,003 | 0,006 | 0,01 | 0,015 | 0,03 | 0,05 | 0,074 | 0,106 | 0,145 | 0,190 | 0,245 | 0,365 | 0,520 | 0,705 | 0,920 | 1,200 | 1,475 | ||||
|
|
|
|
| |||||||||||||||||||
|
|
|
|
| |||||||||||||||||||
|
|
|
|
| |||||||||||||||||||
|
|
|
|
| |||||||||||||||||||
|
|
|
|
| |||||||||||||||||||
Приложение 11
Значения коэффициента шероховатости п естественных и искусственных русел
| Поверхность русла | n | ||
| Естественные русла: Чистое, прямое, незасоренное русло со свободным | |||
| течением (глина, мелкий песок, гравий) | 0,025 | ||
| Периодические потоки в очень хорошем состоянии поверхности и формы ложа, но с заметным | |||
| содержанием наносов Сильно засоренные, извилистые русла с заросшими берегами | 0,033 0,05 | ||
| Русла горноводопадного типа с валунами и извилистым ложем;искривленные равнинные русла с заводями и | |||
| косоструйным течением | 0,10 | ||
| Реки болотного типа; течение с выходом на пойму Искусственные русла: | 0,13 | ||
| Оштукатуренная цементным раствором поверхность | 0,011 | ||
| Бетонная поверхность без затирки | 0,013 | ||
| Металлическая, гладкая | 0,012 | ||
| Деревянная из строганных досок | 0,0,013 | ||
| Кирпичная кладка, покрытая цементным раствором | 0,015 | ||
| Бутовая кладка на цементном растворе | 0,018 | ||
| Мощение булыжным камнем | 0,02 | ||
| Одернованная поверхность | 0,025 | ||
| Каменная наброска в плетнях Каналы в плотном лессе; плотной земле;плотном | 0,025 | ||
| мелком гравии Большие земляные каналы в хороших условиях | 0,017 | ||
| содержания Большие земляные каналы в удовлетворительных | 0,02 | ||
| условиях содержания Малые земляные каналы при полной планировке дна и | 0,025 | ||
| откосов Каналы и русла в скальных породах в средних условиях | 0,0275 | ||
| содержания | 0,03 | ||
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Сборник задач по машиностроительной гидравлике; Учебное пособие для машиностроительных вузов / Д.А. Бутаев, З.А. Калмыкова, Л.Г. Подвидз и др. -М.: Машиностроение, 198L-464c.
2.Примеры расчетов по гидравлике: Учебное пособие для студентов строительных специальностей вузов/ АД. Альтшуль, В.И. Калицун, Ф.Г. Майра-новский, П.П. Палыунов -М.: Стройиздат, 1977,- 255с.
3. Справочное пособие по гидравлике, гидромашинам и гидроприводам /Под общей редакцией Б.Б. Некрасова.-Минск: Вышэйшая школа, 1985.-382с.
4.Альтшуль А.Д., Животовский Л.С., Иванов Л.П. Гидравлика и аэродинамика: Учебник для вузов.-М.: Стройиздат, 1987.-414с.
5.Френкель Н.З. Гидравлика. Учебник для механических и машиностроительных специальностей вузов.-М.;Л.: Госэнергоиздат,1956.- 456с.
6.Задачник по гидравлике, гидромашинам и гидроприводу: Учебное пособие для машиностроительных специальностей вузов/ Под редакцией Б.Б. Не-красова.-М.: Высшая школа, 1989.-192с.
7.Сборник задач по гидравлике: Учебное пособие для вузов/ Под редакцией В.А. Большакова.-Киев: Вища школа, 1979.- 336с.
8.Справочник по гидравлике / Под редакцией В.А. Большакова.- Киев: Вища школа,1984.~ 343с.
9.Сборник заданий для выполнения расчетно-графичеекой работы по курсу "Гидравлика и гидравлические машины и компрессоры"/ Под редакцией АЛЛ. Барекяна.Калинин: Изд. Калининского политехнического института, 1973.-127с.
10.Барекян АЛЛ., Челышев А.К. Задачи по механике жидкости с решениями и рекомендациями по их оформлению: Учебное пособие для студентов, обучающихся по техническим направлениям ТГТУ.-Тверь.: Изд. Тверского государственного технического университета, 1997.-158с.
11.Сборник заданий по гидравлике для гидромелиоративных и гидротехнических факультетов гидромелиоративных институтов./ А.В. Андреевская, Н.Н. Кременецкий, М.В. Панова, Д.В. Штеренлихт. М.: МГМИ,1968.-260с.
12.Андреевская А.В., Кременецкий Н.Н., Панова М.В. Задачник по гидравлике: Учебное пособие для гидромелиоративных и гидротехнических факультетов и вузов.~М.:Энергия,1970.-424с.
13.Дробнис В.Ф. Гидравлика и гидравлические машины: Учебное пособие для студентов пед. инстит. по спец. №2120 "Общетехнические дисциплины и труд".-М.: Просвещение,1987.-191с.
14.Примеры гидравлических расчетов:Учебное пособие для студентов вузов, обучающихся по специальности "Автомобильные дороги"/ А.И. Богомолов, Н.М. Константинов, В.А. Александров, Н.А. Петров - М.: Транспорт, 1977.- 526с.
15.Шевелев Ф.А., Шевелев А.Ф. Таблицы для гидравлического расчета водопроводных труб: Справочное пособие.- М.:Стройиздат, 1984.- 116с.
Содержание
стр.
Введение 3
I. ГИДРОСТАТИКА 4
1. Гидростатическое давление 4
1.1 .Основные теоретические положения и расчетные зависимости 4
1.2.Примеры решения задач 7
1.3 .Задачи для самостоятельного решения 14
2. Сила гидростатического давления
на плоские поверхности 24
2.1 .Основные теоретические положения и расчетные зависимости 24
2.2.Примеры решения задач 27
2.3. Задачи для самостоятельного решения 37
3. Сила гидростатического давления на криволинейные симметричные поверхности постоянной кривизны 52
3.1. Основные теоретические положения и расчетные зависимости 52
3.2. Примеры решения задач 55
3.3 .Задачи для самостоятельного решения 70
II. ГИДРОДИНАМИКА 85
4. Уравнение Д. Бернулли и гидравлические сопротивления 85
4.1. Основные теоретические положения и расчетные зависимости 85
4.2. Примеры решения задач на применение уравнения Д.Бернулли без
учета гидравлических сопротивлений 92
4.3. Примеры решения задач на применение уравнения Д. Бернулли с учетом гидравлических сопротивлений 99
4.4. Задачи для самостоятельного решения 110
5. Гидравлический расчет коротких трубопроводов 140
5.1. Основные типы задач и общие рекомендации по их решению 140
5.2. Примеры решения задач 142
5.3. Задачи для самостоятельного решения 146
6. Гидравлический расчет длинных трубопроводов 188
6.1. Основные расчетные зависимости и типы задач 188
6.2. Примеры решения задач 193
6.3. Задачи для самостоятельного решения 200
7. Гидравлический расчет открытых каналов при равномерном движении
жидкости 206
7.1. Основные расчетные зависимости и типы задач 206
7.2. Примеры решения задач 211
7.3. Задачи для самостоятельного решения 216
Приложения 221 Библиографический список 230 Содержание 231
Дата: 2019-11-01, просмотров: 1032.
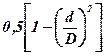
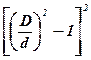
 Обратный клапан (zо.к.)
Обратный клапан (zо.к.)