ГИДРАВЛИЧЕСКИЙ РАСЧЕТ КОРОТКИХ ТРУБОПРОВОДОВ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

5.1. Основные типы задач и общие рекомендации по их решению

Коротким называют трубопровод, в котором местные потери напора соизмеримы с потерями напора по длине, т.е. являются величинами одного порядка, поэтому при гидравлическом расчете коротких трубопроводов вычисляют потери напора по длине и в каждом местном сопротивлении.

Короткий трубопровод может иметь постоянный диаметр по всей длине или же состоять из ряда последовательно соединенных участков разного диаметра.

Короткими трубопроводами являются, например, всасывающие трубопроводы насосных установок, сифонные трубопроводы, дюкеры, донные водоспуски и дорожные трубы (трубопереезды).

Основные уравнения и зависимости, используемые при гидравлическом расчете коротких трубопроводов, рассмотрены в подпункте 4.1.

Наиболее часто встречающиеся в инженерной практике задачи при гидравлическом расчете коротких трубопроводов сведены к трем типам.

Задачи типа I . Определить потребный напор Н_потр (или давление р) в каком-либо живом сечении потока жидкости, если известны расход Q потока жидкости, род жидкости и ее температура, длины l_i всех участков трубопровода и внутренние диаметры d_i труб, материал, из которого изготовлены трубы, и состояние их внутренней поверхности.

Решение. Величину Н_потр (или давление р) определяют прямой подстановкой в уравнение Д. Бернулли заданных параметров, а также величин, предварительно вычисленных (например, средней скорости u). Знание скоростей u _i и диаметра d_i на всех участках трубопровода, а также коэффициента кинематической вязкости v жидкости и абсолютной шероховатости Δ_Э (величины v и Δ_Э берут из справочной литературы) позволяет предварительно установить для каждого участка трубопровода область гидравлического сопротивления и на этой основе определить коэффициенты λ и ζ.

Задачи типа II . Определить расход жидкости Q и (или) среднюю скорость u в каком-либо сечении потока, если известны потребный напор Н_потр, род жидкости и ее температура, материал труб и состояние их внутренней поверхности, длины всех участков трубопровода l_i и внутренние диаметры d_i труб.

Решение. Величину Q и (или) u определяют из уравнения
Д. Бернулли путем последовательных приближений.

Не имея возможности, из-за незнания Q (или u), заранее установить для каждого участка трубопровода режим течения и область гидравлического сопротивления, предполагают, что все участки трубопровода работают в области квадратичного сопротивления, где коэффициенты λ и ζ не зависят от числа Рейнольдса (в этом случае λ зависит только от Δ_Э/ d , a ζ – от вида местного сопротивления). Затем решают уравнение Д. Бернулли относительно искомой величины и получают ее первое приближение Q ₁ (или u₁). Далее, зная Q ₁ (или u ₁), определяют, в какой области гидравлического сопротивления в действительности будет работать каждый участок рассчитываемого трубопровода.

Если выяснится, что все участки работают в области квадратичного сопротивления, найденную величину Q ₁ (или u ₁) считают окончательной, т.е. принимают за расчетную. Если какие-либо участки трубопровода (или какой-нибудь один участок) работают в других областях гидравлического сопротивления (доквадратичной или гладких труб), вычисляют для этих участков по соответствующим эмпирическим формулам более точные значения коэффициента λ и, подставив их в уравнение Д. Бернулли, находят величину расхода (или средней скорости) во втором приближении Q ₂ (или u ₂). Эти величины считают окончательными.

Задачи типа III . Определить внутренний диаметр d (или длину l) одного из участков трубопровода, если известны расход потока жидкости Q _необх , род жидкости и ее температура, потребный напор Н_потр, материал труб и состояние их внутренней поверхности, внутренние диаметры d_i (или длины l_i) остальных участков.

Задачи этого типа можно решить только подбором. Для уменьшения числа попыток задачи решают обычно графоаналитическим методом с построением графика Q = f ( d ) или Q = f ( l ) и находят по нему величину d (или l).

Пример оформления графика Q = f ( d ) см. на рис. 4.14 и 5.8. При расчете коротких трубопроводов, независимо от типа решаемых задач, рекомендуется излагать решение в такой последовательности:

выбирают и обозначают на расчетной схеме трубопровода (рис. 5.1) два живых сечения потока (I-I и II-II), в каждом из которых должно быть известно не менее двух слагаемых трехчлена ( z +p/ρg+ a u ² /2 g ), и плоскость сравнения 0-0 . Целесообразно совмещать плоскость сравнения с центром тяжести одного из выбранных живых сечений (в этом случае величина z ₁ или z ₂ становится равной нулю);

записывают уравнение Д. Бернулли в общем виде;

конкретизируют слагаемые уравнения Д. Бернулли применительно к условиям решаемой задачи и принятым обозначениям величин;

записывают уравнение Д. Бернулли для выбранных живых сечений потока применительно к условиям решаемой задачи с учетом высотного расположения выбранной плоскости сравнения;

решают уравнение Д. Бернулли относительно искомой величины, делая необходимые алгебраические преобразования и табулируя расчеты, необходимые для построения графика Q = f ( d ) или Q = f ( l );

вычислив скоростные напоры, а также потери напора по длине на каждом участке трубопровода и потери напора в каждом местном сопротивлении, строят в масштабе график напоров (диаграмму уравнения Д. Бернулли). Примеры оформления графика напоров см. на рис. 5.2, 5.4, 5.6, 5.9 и 5.11.

Примеры решения задач

Задача 5.3.1. Трубопровод, соединяющий открытые резервуары А и Б (рис. 5.1), должен обеспечивать пропуск расхода воды Q = 0,017 м³/с при температуре t = 20 ° C . Трубы стальные, умеренно заржавленные. Длины участков трубопровода l ₁ = 80 м, l ₂ = 40 м, внутренние диаметры труб соответственно d ₁ = 0,125 м, d₂ = 0,080 м. Угол открытия пробкового (конического) крана, расположенного в середине второго участка, a = 25°.

Определить перепад уровней воды Н в резервуарах и построить диаграмму уравнения Д. Бернулли (график напоров).

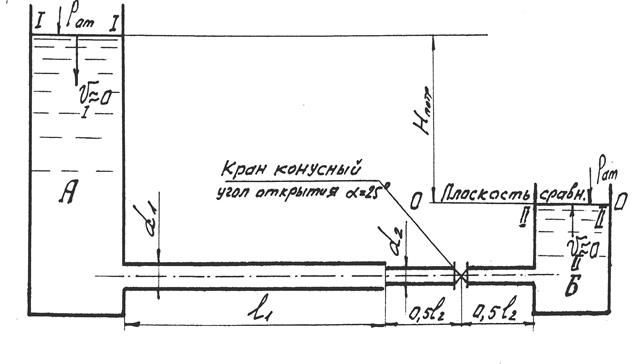
Рис. 5.1. Схема к гидравлическому расчету короткого трубопровода
(к задаче 5.3.1)

Решение. Данная задача относится к типу I. Искомый перепад уровней воды Н, когда резервуары открыты, является потребным напором Н_потр. Для определения величины Н = Н_потр свяжем уравнением
Д. Бернулли два живых сечения потока (I-I и II-II) и решим его относительно искомой величины Н_потр. Выбор живых сечений I-I и II-II плоскости сравнения 0-0 осуществляем, руководствуясь рекомендациями, изложенными на с. 47, 56, 58, 60, 63 пособия. Согласно этим рекомендациям в живых сечениях потока, связываемых уравнением
Д. Бернулли, должно быть известно наибольшее число слагаемых трехчлена (z+ p /ρ g + a u ² /2 g ), по сравнению с другими сечениями, а плоскость сравнения целесообразно совмещать с центром тяжести любого из выбранных сечений.

Применительно к условиям данной задачи для нахождения Н_потр необходимо связать уравнением Д. Бернулли сечения, совпадающие c уровнями воды в резервуарах А и Б, а плоскость сравнения провести через центр тяжести сечения II-II (см. рис. 5.1). В сечениях, совпадающих с уровнями воды в резервуарах, известны давление (равно атмосферному р_ат) и средние скорости (их можно приближенно считать равными нулю, u ₁ » 0 и u ₂ » 0, поскольку площади поперечного сечения резервуаров во много раз больше площадей поперечного сечения трубопровода). Кроме того, для сечения II-II z₂ = 0.

По условиям данной задачи слагаемые уравнения Д. Бернулли будут иметь вид

z ₁ = H _потр ; p ₁ / ρ g = p _ат /ρ g ; a ₁ u ₁ ² / 2 g » 0;

z ₂ = 0; p ₂ / ρ g = p _ат /ρ g ; a ₂ u ₂ ² / 2 g » 0;

h_W _1-2 = S h_l + S h _м = h_l ₁ + h_l ₂ + h _вх + h _р.с + h _кр + h _вых .

Здесь h_l ₁ , h_l ₂ – потери напора по длине на первом и втором участках;

h _вх , h _р.с , h _кр , h _вых – соответственно потери напора в местных сопротивлениях при входе потока в трубопровод из резервуара, при резком сужении трубопровода, в кране, при выходе потока из трубопровода в резервуар (истечение под уровень).

Записав уравнение Д. Бернулли для условий задачи, выразив при этом потери h ₁ и h _м по формулам (4.11) и (4.12), и решив его относительно искомой величины Н_потр, получим

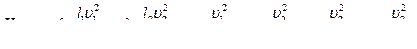(5.1)

Далее вычислим величину Н_потр прямой подстановкой входящих в выражение (5.1) величин, предварительно найдя:

а) средние скорости u ₁ и u ₂ на участках из уравнения (4.6);

б) коэффициенты гидравлического трения λ₁ и λ₂ по эмпирическим формулам с учетом области гидравлического сопротивления,

определяемой по числу Рейнольдса R е и относительной шероховатости
Δ_Э/ d (с использованием граничных чисел Рейнольдса (см.с.74 пособия);

в) величины коэффициентов ζ_вх, ζ_р._с, ζ_кр, ζ_вых находим в
приложении 6:

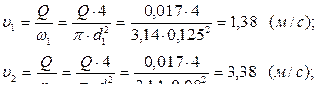
ζ_вх= 0,5 – для острых входных кромок;

ζ _р. _c вычислим по эмпирической формуле Идельчика (см. приложение 6):

ζ_р.с = 0,5(1 – d ₂ ² / d ₁ ² ) = 0,5(1 – 1,125² / 0,08²) = 0,30;

ζ_кр = 3,45; ζ_вых = 1,0.

С целью установления областей гидравлического сопротивления вычислим для каждого участка величину Re по формуле (4.9) и относительную шероховатость Δ_Э/ d, найдя в приложениях 1 и 4 коэффициент кинематической вязкости v воды при t = 20 °С
(v = 1,01 · 10^-6м²/с) и абсолютную эквивалентную шероховатость
(Δ_Э = 0,5 мм ).

Для первого участка трубопровода

Для второго участка трубопровода

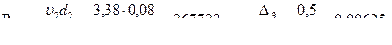
Поскольку Re ₁ и Re ₂ больше критического числа Рейнольдса
( Re _кр = 2320), режим движения воды в трубопроводе турбулентный. Далее найдем величины граничного числа Рейнольдса Re _кв = 500d / Δ_Э для каждого участка трубопровода, отвечающие началу их работы в области квадратичного сопротивления:

для первого участка Re _кв1 =500 d ₁ / Δ_Э =500 ∙ 125 / 0,5 = 125000,

для второго участка R е_кв2 = 500 d ₂ / Δ_Э = 500 ∙ 80 / 0,5 = 80000.

Исходя из того, что Re ₁ = 170792 > Re _кв1 = 125000 и Re ₂ = 267723 > Re _кв2 = 80000, приходим к выводу, что оба участка будут работать в области квадратичного сопротивления, поэтому коэффициенты λ₁ и λ₂ вычислим по формуле (4.16):

λ₁ = 0,11(Δ_Э / d ₁ )^0,25 = 0,11 ∙ 0,004^0,25 = 0,028;

λ₂ = 0,11(Δ_Э / d ₂ )^0,25 = 0,11 ∙ 0,00625^0,25 = 0,031.

Подставив заданные и найденные величины в выражение (5.1), вычислим величину потребного напора;

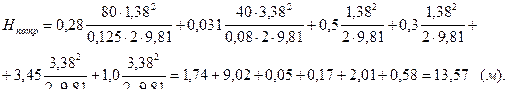
Построение графика напоров. График напоров, включающий в себя линию полного напора и пьезометрическую, показывает изменение по длине трубопровода полного напора потока и его составляющих.

Для построения графика вычерчиваем в искаженном масштабе трубопровод (рис. 5.2) и показываем на нем выбранные живые сечения потока I-I и II-II, совпадающие с уровнями воды в резервуарах А и Б, а также плоскость сравнения 0-0. Поскольку резервуары открытые, уровни воды в них являются одновременно пьезометрическими уровнями.

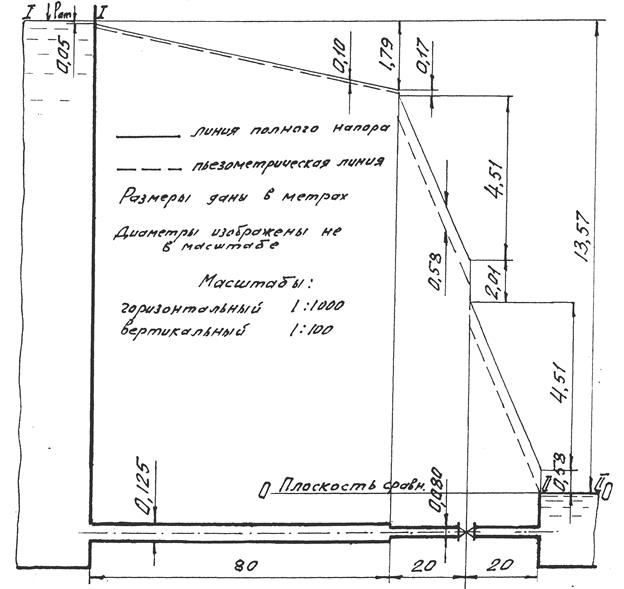
Рис. 5.2. График напоров (диаграмма уравнения Бернулли, к задаче 5.3.1)

Линию полного напора (полной удельной механической энергии потока) строим, последовательно вычитая потери напора, нарастающие вдоль потока, из начального напора потока (заданного в нашем случае пьезометрическим уровнем в питающем резервуаре А), равного
Н_потр= 13,57 м.

Пьезометрическую линию, показывающую изменение гидростатического напора потока, строим, вычитая из полного напора в рассматриваемых сечениях потока скоростные напоры.

Для упрощения построения графика напоров условно считаем, что местная потеря h _м напора в любом местном сопротивлении сосредоточена в живом сечении потока, где расположено местное сопротивление.

Для построения линии полного напора вычитаем из начального напора Н_потр = 13,57 м потерю напора при входе потока в трубопровод
h _вх = 0,05 м и получаем полный напор в начале первого участка трубопровода: 13,57 – 0,05 = 13,52 м. Чтобы найти полный напор в конце первого участка трубопровода, вычитаем из первоначального напора
Н_потр= 13,57 м сумму двух потерь напора (при входе h _вх = 0,05 м и по длине первого участка h_l ₁ = 1,74), т.е. 13,57 – (0,05 + 1,74) = 11,78 (м).

Для нахождения полного напора в начале второго участка вычитаем из Н_потр сумму трех потерь напора ( h _вх + h_l ₁ + h_p . _c ) и получаем
13,57 – (0,05 + 1,74 + 0,17) = 11,61(м).

Аналогично найдем следующие величины полного напора:

перед краном:

13,57 – (0,05 + 1,74 + 0,17 + 9,02 ∙ 0,5) = 7,10 (м);

непосредственно за краном:

13,57 – (0,05 + 1,74 + 0,17 + 9,02 ∙ 0,5 + 2,01) = 5,09 (м);

в конце 2-го участка, т.е. перед выходом из трубопровода в резервуар Б:

13,57 – (0,05 + 1,74 + 0,17 + 9,02 + 2,01) = 0,58 (м);

непосредственно за выходом, т.е. в резервуаре Б:

13,57 – (0,05 + 1,74 + 0,17 + 9,02 + 2,01 – 0,58) = 0,00 (м).

Как видим, в открытых резервуарах потребный напор Н_потр целиком затрачивается на преодоление потерь напора в трубопроводе:

Н_потр = Sh_W _1-2 = S h_l + S h _м .

Откладываем в масштабе полученные полные напоры в рассмотренных живых сечениях потока и, учитывая, что движение воды на участках равномерное, соединяем прямыми линиями концы отрезков, выражающих полные напоры в начале и в конце каждого участка. Получаем линию полного напора (см. рис. 5.2).

Для построения пьезометрической линии откладываем от построенной линии полного напора вертикально вниз величины скоростных напоров u ₁ ² / 2 g = 0,1 м на первом участке, и u ₂ ² / 2 g = 0,58 м на втором участке и, проведя через концы отрезков, выражающих

скоростные напоры, линии, параллельные линии полного напора, получим пьезометрическую линию (см. пунктирную линию на рис. 5.2).

Задача 5.3.2. Вода сливается из бака А в атмосферу по трубопроводу, состоящему из двух участков. Трубы стальные, новые. Диаметр труб на первом участке d ₁ = 0,08 м, на втором d ₂= 0,05 м. Длина первого участка l ₁ =10 м, второго l ₂ = 5 м (рис. 5.3). Посередине второго участка имеется вентиль, открытый полностью. Превышение уровня воды в резервуаре А над центром тяжести выходного сечения трубопровода
Н = 9,5 м. Температура воды t = l5 °C.

Определить, какой расход воды Q пропустит трубопровод? Построить график напоров.

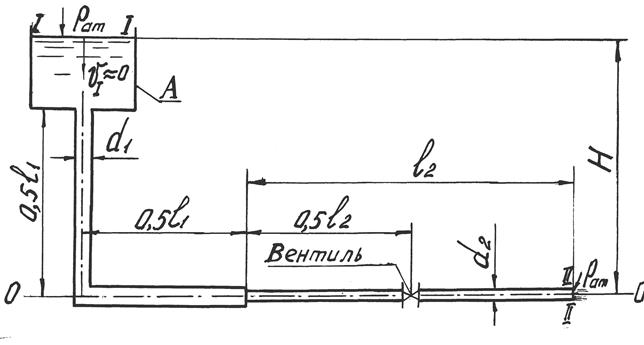
Рис. 5.3 .Схема к гидравлическому расчету короткого трубопровода
(к задаче 5.3.2)

Решение. Задача относится к типу II, поэтому расход воды Q может быть найден только путем последовательных приближений. Определяя величину расхода Q в первом приближении, будем полагать, что трубопровод работает в области квадратичного сопротивления (в этом случае коэффициенты λ и ζ не зависят от числа Рейнольдса Re ).

Для нахождения величины Q применим уравнение Д. Бернулли к живым сечениям потока I-I и II-II (см. рис. 5.3), приняв за плоскость сравнения 0-0 плоскость, проходящую через центр тяжести сечения II-II, т.е. через центр тяжести выходного сечения трубопровода. Сечение I-I совмещаем со свободной поверхностью воды в баке А. Выбор именно этих сечений обусловлен тем, что в них известно наибольшее число слагаемых

трехчлена ( z + p /ρ g + a u ² /2 g ), по сравнению с остальными живыми сечениями потока. Действительно, в сечении I-I известны все три слагаемые трехчлена ( z ₁ = H ; p ₁ / ρ g = p _ат / ρ g ; a ₁ u ₁ ² / 2 g » 0, т.к. площадь бака А во много раз превышает площадь поперечного сечения трубопровода). В сечении II-II известны два слагаемых:

z ₂ = 0; p ₂ /ρ g = p _ат / ρ g .

Применительно к условиям данной задачи уравнение Д. Бернулли примет вид

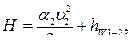(5.2)

где a – коэффициент Кориолиса в сечении II-II (примем a₂ ≈ 1,0);

u₂ – средняя скорость движения потока в сечении II-II;

h_W _1-2 = S h_l + S h _м – суммарные потери полного напора в трубопроводе. Для условий данной задачи

h_W _1-2 = h_l ₁ + h_l ₂ + h _вх + h_p _.кол + h_p _. _c + h _в .

Здесь h_l ₁ и h_l ₂ – потери напора по длине на первом и втором участках трубопровода;

h _вх – потеря напора на вход;

h_p _.кол – потеря напора в колене без закругления с поворотом на 90⁰;

h_p _. _c – потеря напора при резком сужении трубопровода;

h _в – потеря напора в полностью открытом вентиле.

Выразив входящие в уравнение (5.2) потери напора согласно формулам (4.11) и (4.12), а средние скорости – в соответствии с уравнением (4.6), получим

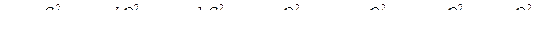Решив это выражение относительно расхода Q, получим зависимость

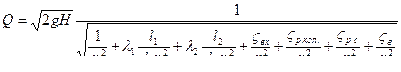. (5.3)

Полагая работу трубопровода в области квадратичного сопротивления, вычислим коэффициенты гидравлического трения λ₁ и λ₂ по формуле (4.16), приняв абсолютную шероховатость труб, согласно приложению 4 (Δэ = 0,10 мм), и получим

λ₁ = 0,11(Δ_Э / d ₁ )^0,25 = 0,11 ∙ (0,10 / 80)^0,25 = 0,021;

λ₂ = 0,11(Δ_Э / d ₂ )^0,25 = 0,11 ∙ (0,10 / 50)^0,25 = 0,023.

Коэффициенты местного сопротивления найдем в приложении 6
(ζ_вх = 0,5 ; ζ_р.кол. = 1,26; ζ_р._с. = 0,30 ; ζ_в = 4,6) и определим площади ω₁ и ω₂ поперечного сечения трубопровода на первом и втором участках:

ω₁ = (3,14 ∙ 0,08²) / 4 = 0,00502 (м²); ω₂ = (3,14 ∙ 0,05²) / 4 = 0,00196 (м²).

Подставив заданные и найденные величины в зависимость (5.3), получим величину расхода воды в первом приближении:

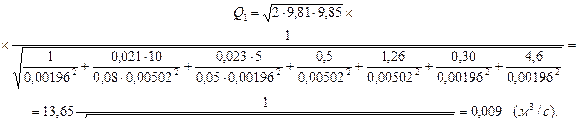
Выясним, в какой области гидравлического сопротивления в действительности будет работать каждый участок трубопровода. С этой целью по формуле (4.9) вычислим для участков трубопровода числа Рейнольдса Re ₁ и Re ₂ и сравним их с величинами Re _кв1 и Re _кв2 граничного числа Рейнольдса, вычисляемого по формуле ( Re _кв = 500 d / Δ_Э), т.е. с величинами Re , отвечающими началу работы участков трубопровода в области квадратичного сопротивления.

Если Re ₁ и Re ₂ окажутся больше Re _кв1 и Re _кв2 , значит оба участка будут действительно работать в области квадратичного сопротивления.

Вычисляем числа Рейнольдса, предварительно найдя в приложении 1 величину коэффициента кинематической вязкости v воды при 15 °С
(v = 1,12 10^-6 м²/с):

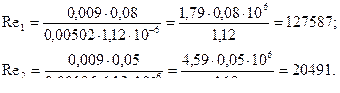
Определяем граничные числа Рейнольдса Re _кв1 и R е_кв2:

Re _кв1 = (500 ∙ 80) / 0,10 = 400000 ;

Re _кв2 = (500 ∙ 50 ) / 0,10 = 250000.

Поскольку Re ₁ < Re _кв1 и Re ₂ < Re _кв2 , оба участка не будут работать в области квадратичного сопротивления.

Для установления области сопротивления вычислим граничное число Рейнольдса Re _гл = 10 / Δ_Э, отвечающее началу работы трубопровода в области гидравлически гладких труб:

Re _гл1 = (10 ∙ 80) / 0,10 = 8000 ;

Re _кв2 = (10 ∙ 50 ) / 0,10 = 5000.

Так как Re ₁ > Re _гл1 и Re ₂ > Re _гл2 , оба участка будут работать в области доквадратичного сопротивления. Далее вычислим расход воды во втором приближении Q ₂ , найдя предварительно коэффициенты гидравлического трения λ₁ и λ₂ по формуле А.Д. Альтшуля (4.15) для области доквадратичного сопротивления :

λ₁ = 0,11 ∙ (0,10 / 80 + 68/127857)^0,25 = 0,023;

λ₂ = 0,11 ∙ (0,10 / 50 + 68/204911)^0,25 = 0,024;

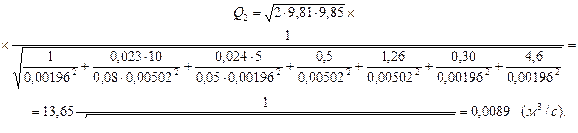Величину Q ₂ считаем искомой величиной расхода,
Q ₂ = Q = 0,0089 (м³/с).

Для построения графика напоров предварительно подсчитаем потери напора по длине и скоростные напоры на участках, а также потери напора в каждом местном сопротивлении:

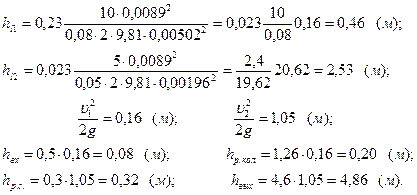
Линию полного напора (полной удельной энергии потока) найдем, последовательно вычитая потери напора, нарастающие вдоль потока, из начального напора, заданного пьезометрическим уровнем в баке А (в данном случае этот уровень совпадает со свободной поверхностью воды в баке). Пьезометрическую линию получим на основе вычитанием скоростного напора из полного напора в рассматриваемых живых сечениях потока.

Приняв масштабы: горизонтальный 1:50 и вертикальный 1:25, – строим график напоров (рис 5.4).

Задача 5.3.3. Определить, какое манометрическое давление р_л необходимо создать в левом резервуаре (рис. 5.5), чтобы подать в правый резервуар, находящийся под манометрическим давлением р _n = 20 кПа, расход Q = 0,020 м³/с при t = 10 °С по трубопроводу, состоящему из двух участков l ₁ = 30 м, l ₂ = 20 м, при диаметре труб d ₁ = 0,10 м и d ₂ = 0,15 м. В середине второго участка установлена простая задвижка, степень открытия которой a / d = 0,5. Трубы стальные, нормальные. Глубина воды в левом резервуаре h _л = 2,5м, в правом h_n = 1,5 м. Построить график напоров.

Решение. Манометрическое давление р_л на свободной поверхности воды в левом резервуаре определим прямой подстановкой величин в уравнение Д. Бернулли.

С учетом рекомендаций, изложенных в подпункте 4.1, выбираем живые сечения потока I-I и II-II, для которых запишем уравнение (4.4), и плоскость сравнения 0-0. Для условий данной задачи сечение I-I совместим с уровнем воды в левом резервуаре, а сечение II-II – в правом, т.к. именно в этих живых сечениях потока известно наибольшее число слагаемых трехчлена ( z + p /ρ g + a u ² /2 g ). Плоскость сравнения совместим с осью трубопровода. Применительно к условиям задачи уравнение
Д. Бернулли примет вид

h _л +р_л / ρ g = h _п + p _п / pg + h_W _1-2 . (5.4)

Решая его относительно искомой величины, получим

р_л=( h _п – h _л +р_п / ρ g + h_W _1-2 )∙ρ g = (1,5 – 2,5 + 20000 / (1000∙ 9,81) +

+ h_W _1-2 )∙1000 ∙ 9,81 = (1,04+ h_W _1-2 ) = 9810 (Па).

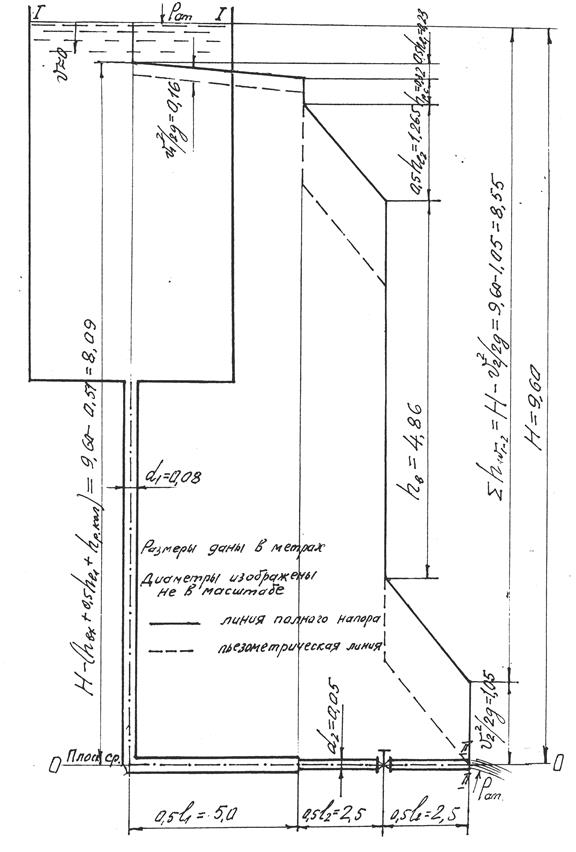
Рис. 5.4. График напоров (к задаче 5.3.2)

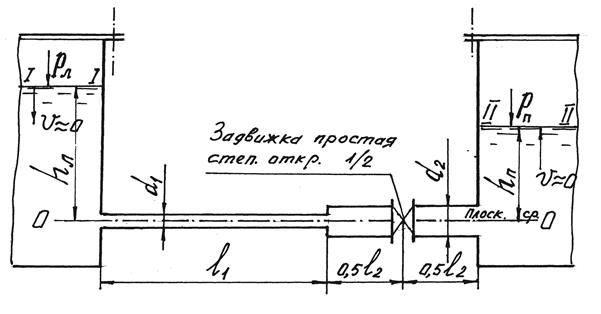
Рис. 5.5. Схема к гидравлическому расчету короткого трубопровода
(к задаче 5.3.3)

Как видим, задача по определению величины р_л сводится к вычислению потерь напора h_W _1-2 , т.е. потерь напора по длине и местных. Для нашего случая

h_W _1-2 = h_l ₁ + h_l ₂ + h _вх + h_p _. _p + h ₃ + h _вых .

Здесь h_l ₁ и h_l ₂ – потери напора по длине на первом и втором участках трубопровода;

h _вх – потеря напора на вход;

h_p _. _p – потеря напора при резком расширении трубопровода;

h ₃ – потеря напора в задвижке;

h _вых – потеря напора при выходе потока из трубопровода в резервуар (истечение под уровень).

Выражая потери напора по длине и местные по формулам (4.11) и (4.12), а средние скорости через расход Q, по формуле (4.6), получим выражение для вычисления давления р_л :

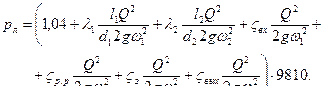(5.5)

В правой части выражения (5.5) не известны только коэффициенты гидравлического трения λ₁ и λ₂ и коэффициенты местных сопротивления ζ_вх, ζ_р.р, ζ_з, ζ_вых.

Коэффициенты λ₁ и λ₂ вычислим по эмпирическим формулам, установив предварительно, в какой области гидравлического сопротивления будет работать каждый участок трубопровода. Величины коэффициентов местных сопротивлений найдем в приложении 6.

Для установления области гидравлического сопротивления вычислим по формуле (4.9) для каждого участка число Рейнольдса Re и, если оно окажется больше критического (Re _к _p = 2320), найдем относительную шероховатость Δ_Э/ d (величину абсолютной эквивалентной шероховатости Δ_Э возьмем в приложении 4, Δ_Э = 0,19 мм). Далее, имея для каждого участка Re и Δ_Э / d, по графику Г.А. Мурина (см. приложение 5) установим область гидравлического сопротивления и выберем соответствующие формулы для вычисления коэффициентов λ₁ и λ₂:

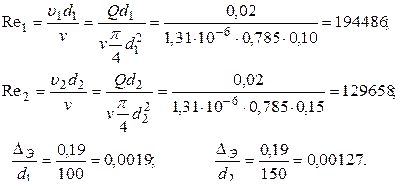
Обратившись к графику Г.А. Мурина, приходим к выводу, что оба участка будут работать в области доквадратичного сопротивления, поэтому коэффициенты λ₁ и λ₂ вычислим по формуле (4.15):

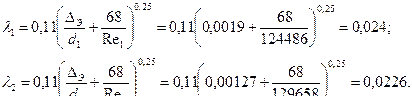
Коэффициенты местноых сопротивлений:

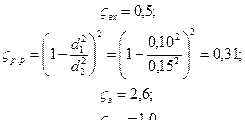
Подставив в выражение (5.5) заданные величины, а также найденные значения коэффициентов гидравлического трения и местных сопротивлений, вычислим величину р_л:

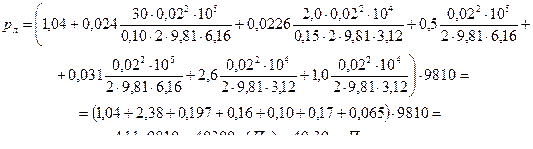
Для построения графика напоров, включающего в себя линию полного напора и пьезометрическую, вычислим величину начального напора, т.е. полного напора в сечении I-I. Этот напор равен

Н _I _- _I = h _л + р_л/ρ g = 2,5 + 40300/1000 ∙ 9,81 = 2,5 + 4,11 = 6,61 (м).

Затем, исходя из величины начального напора и длины трубопровода, принимаем горизонтальный и вертикальный масштабы (М_г 1:500, М_в 1:50). Вычерчиваем трубопровод (диаметры труб изображаем не в масштабе) и показываем на чертеже величину начального напора Н _I _- _I, определяемую положением пьезометрического уровня в левом резервуаре, после чего строим линию полного напора на основе последовательного вычитания из величины Н _I _- _I потери напора, нарастающие вдоль потока.

Непосредственно за входом в трубопровод, в начале первого участка, полный напор

Н_{науч.уч.1} = Н _I _- _I – h _вх = 6,6 1 – 0,16 = 6,45 (м).

Непосредственно перед расширением трубопровода, в конце первого участка,

Н_науч _. _уч _.1 = Н _I-I – (h _вх + h_I-I) = 6,6 1 – (0,16 +2.38) = 4,07 ( м ).

Непосредственно за расширением трубопровода, в начале второго участка,

Н_науч _. _уч _.2 = Н _I-I – (h _вх +h_I-I +h_p.p) = 6,6 1 – (0,16 + 2,38 + 0,10) = 3,97 ( м ).

Непосредственно перед задвижкой

Н_{науч.уч.2} = Н _I _- _I – ( h _вх + h_I _- _I + h_p _. _p + 0,5 h ₁₂ ) =

=6,61 – (0,16 + 2,38 + 0,10 + 0,10) = 3,87 (м).

Непосредственно за задвижкой

H _з.з. = 6,61 – (0,16 + 2,38 + 0,10 + 0,10 + 0,17) = 3,70 (м).

Перед выходом из трубопровода в резервуар, в конце второго участка.

Н_к.уч.₂= 6,6 1 – (0,16 + 2,38 + 0,10 + 0,20 + 0,17) = 3,60м.

Конечный напор, т.е. напор в сечении II-II

Н _II-II = H_I-I –h_W1-2 = 6,6 1 – (0,16 + 2,38 + 0,1 + 0,2 + 0,17 + 0,07) =

= 6,61 – 3,07 = 3,54 (м).

Пьезометрическую линию строим на основе вычитания скоростного напора из полного напора в указанных выше живых сечениях потока. Поскольку движение воды на участках равномерное, пьезометрическая линия на каждом участке будет параллельна линии полного напора.

Построенный график напоров представлен на рис.5.6.

Задача 5.3.4. Определить величину стандартного диаметра d сифонного трубопровода (рис. 5.7), по которому необходимо подавать расход воды Q = 0,050 м³/с из водоема А в водоем В при условии, чтобы вакуумметрическая высота h _вак в наиболее опасном сечении (см. сеч. 3-3 на рис. 5.7) не превышала 6,5 м вод.ст. Заметим, что сечение 3-3 расположено после поворота. Превышение центра тяжести сечения 3-3 над уровнем воды в питающем водоеме h = 3,0 м. Разность уровней воды в водоемах
H = 2,0 м. Общая длина сифонного трубопровода l = 58 м. Радиус закругления поворота R _п=d. Глубины погружения входного и выходного сечений трубопровода равны: h ₁ = 2,0 м; h ₂ = 1,0 м. Трубопровод снабжен обратным клапаном с сеткой и задвижкой Лудло, степень открытия которой а / d = 1,0. Задвижка расположена в середине нисходящей линии сифона. Трубы чугунные, нормальные, Δ_Э= 1,0 мм, (см. приложение 4). Температура воды 15 °С, v = l,15 10 ^-6 м²/с (см. приложение 1).

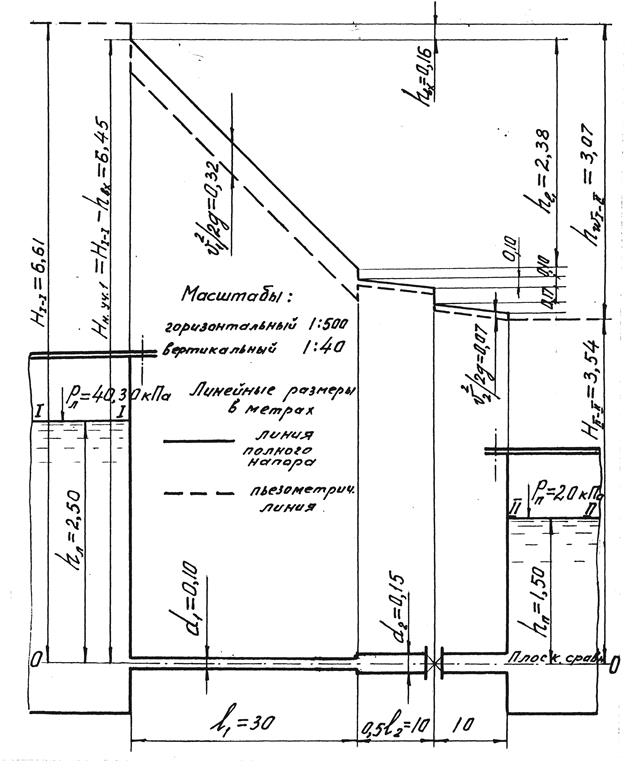
Рис. 5.6. График напоров (к задаче 5.3.3)

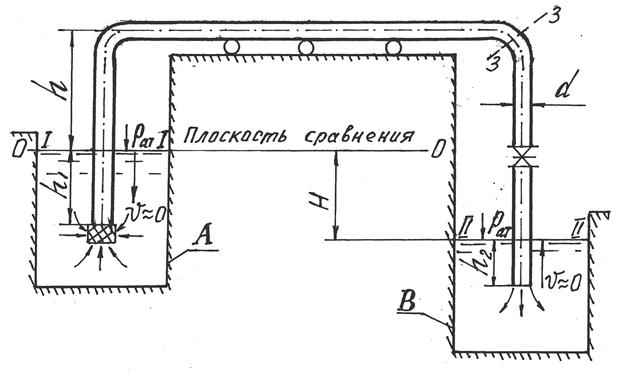
Рис. 5.7. Схема к гидравлическому расчету сифонного трубопровода

(к задаче 5.3.4)

Решение. Для определения диаметра трубопровода с учетом поставленного условия (в сечении 3-3 h _вак £ 6,5 м вод.ст.) применим уравнение Д. Бернулли к живым сечениям потока I-I (совпадает с уровнем воды в водоеме А) и 3-3, где ограничена величина вакуума, приняв за плоскость сравнения 0-0 плоскость, совпадающую с уровнем воды в водоеме А, т.е. с сечением I-I. Для этих условий слагаемые уравнения
Д. Бернулли будут иметь вид

z ₁ = 0; p _1изб = 0; a ₁ u ₁ ² / 2 g » 0;

p _2изб / ρ g = p _вак /ρ g = –р_изб / ρ g ;

a u ₂ ² / 2 g = a u 2 / 2 g ;

h_W _1-2 = h_W _1-3 = h_l _1-3 +2 h _кл.п. + h _кл.с .

а уравнение Д. Бернулли примет вид

0 = h – p _изб / ρ g + a u ² / 2 g + h_l _1-3 + 2 h _пл.п + h _кл.с (5.6)

Приняв a = 1,0, подставив числовые значения величин и выразив потери по длине и местные по формулам (4.11) и (4.12), учитывая формулу (4.6), получим

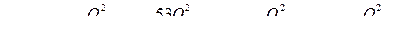(5.7)

Решив уравнение (5.7) относительно расхода Q , получим зависимость, которой можно воспользоваться для определения диаметра d графоаналитическим методом, с построением графика Q = f ( d ), полагая работу трубопровода в области квадратичного сопротивления:

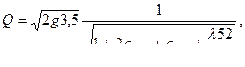
или, в более удобной для расчетов форме,

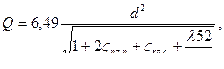(5.8)

Для определения необходимой величины диаметра примем несколько (не менее четырех) произвольных стандартных значений диаметра d и вычислим отвечающие им значения расхода Q . При этом будем задаваться такими величинами d , чтобы получать величины расхода Q и меньше, и больше заданного. Результаты вычислений представим в виде табл. 5.1.

Таблица 5.1

Результаты вычислений для построения графика Q = f ( d )

Внутренний диаметр d, м	0,10	0,15	0,20	0,25
λ = 0,11 (Δ_Э/ d )^0,25	0,035	0,031	0,029	0,028
ζ_кл.с = f ( d ), см. приложение 6	7	6	5,2	4,4
Коэфф. сопротивления колена с закруглением ( a = 90⁰) ζ_кл. _n = f ( d ), см. приложение 6	0,5	0,45	0,3	0,30
Расход воды Q , м³/с	0,0115	0,031	0,0634	0,109

По данным табл. 5.1 построен график зависимости расхода воды Q от внутреннего диаметра d трубопровода (рис. 5.8), из которого видно, что диаметр, отвечающий заданному расходу, d_иск = 0,182 м.

За расчетный диаметр принимаем ближайший больший стандартный
d = 0,20 м (значения стандартных диаметров d труб см. в приложении 10).

Для построения графика напоров вычислим потери напора по длине и в каждом местном сопротивлении при расчетном диаметре труб d = 0,20 м, предварительно установив с помощью графика Г.А. Мурина
(см. приложение 5) область гидравлического сопротивления, в которой будет работать трубопровод.

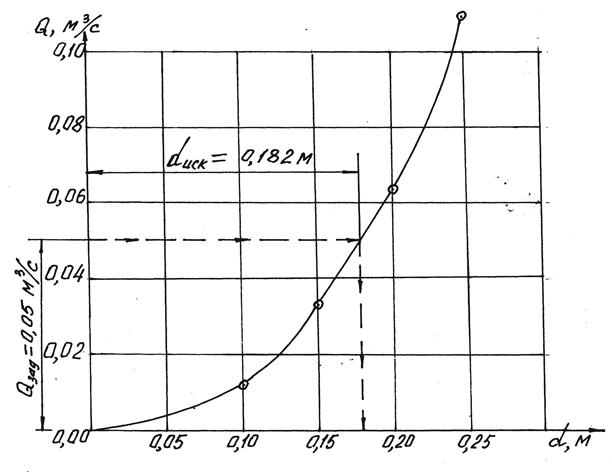
Рис. 5.8. График зависимости расхода воды Q от диаметра трубопровода d (к задаче 5.3.4)

С этой целью вычислим по формуле (4.9) число Рейнольдса Re и относительную шероховатость Δ_Э/ d_p . Предварительно определим среднюю скорость потока:

u = Q / ω = 0,050 ∙ 4 / 3,14 ∙ 0,2²= 1,59 (м/с).

Число Рейнольдса

Re = 1,59 ∙ 0,20 / 1,15 ∙ 10^-6 = 276932,

Δ _Э / d_p _. = 1,0/200 = 0,005.

Обратившись к графику Мурина, убеждаемся, что трубопровод работает в области квадратичного сопротивления.

Для удобства вычисления потерь напора (по длине и местных) определим величину скоростного напора u ² / 2 g = 1,59² / 2 ∙ 9,81 = 0,13 м, через который и выразим потери полного напора h_W _1-2 для решаемой задачи:

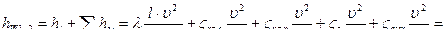
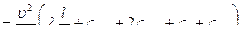
Здесь ζ_з – коэффициент сопротивления полностью открытой задвижки,

ζ₃= 0,15 (см.приложение 6);

ζ_вых – коэффициент сопротивления при выходе потока из трубопровода в водоем, ζ_вых = 1,0.

h_W _1-2 = 0, 13 ∙ (0,029 ∙ 58 / 0,2 + 5,2 + 2 ∙ 0,33 + 0,15 + 1) = 2,0 (м).

Заметим, что для условий данной задачи суммарные потери напора должны быть равны разности уровней воды в водоемах Н. Это следует из уравнения Д. Бернулли, если его записать для сечений I-I и II-II
(см. рис.5.7). Итак, h ₁ = 1,09 м (в том числе на горизонтальном участке
0,88 м); h _кл.с = 0,68 м; 2 h_n _л. _n = 0,08 м ; h ₃ = 0,02 м; h _вых = 0,13 м. Располагая этими данными, выбираем масштабы (горизонтальный 1:500, вертикальный 1:25) и строим график напоров (рис. 5.9), зная из вышеизложенного, что в данном случае начальный напор Н_нач, т.е. напор в сечении I-I при плоскости сравнения, совпадающей с сечением II-II, составляет 2 метра, а конечный напор Н_кон, т.е. в сечении II-II, равен нулю.

Сначала построим линию полного напора, вычитая из его начальной величины потери, нарастающие по пути потока.

Пьезометрическую линию получим, вычитая из полного напора в рассматриваемых сечениях скоростной напор.

Задача 5.3.5. Центробежный насос забирает из резервуара (рис. 5.10) воду. Расход воды Q = 0,018 м³/с, температура t = 15°С. Вакуумметрическое давление перед входом в насос, показываемое вакуумметром В, составляет р_вак = 50 кПа. Общая длина всасывающего трубопровода l = 30 м. Трубы чугунные нормальные с внутренним диаметром d = 0,15 м. На трубопроводе имеются: обратный клапан с сеткой, плавный поворот на 90° радиусом R_n = 2 d = 0,30 м и задвижка Лудло, степень открытия которой a / d = 0,5.

Определить высоту установки насоса Н_вс, т.е. превышение горизонтальной оси насоса над уровнем воды в резервуаре, и построить график напоров. Глубина погружения входного сечения всасывающего трубопровода h _вс = 1,5 м.

Решение. Величину Н_вс найдем прямой подстановкой величин в уравнение Д. Бернулли (4.4), поскольку Q и d заданы. Применительно к условиям задачи уравнение Д. Бернулли запишем для сечений I-I (совпадает с уровнем воды в резервуаре) и II-II (перед входом в насос, там, где подключен вакуумметр), приняв за плоскость сравнения горизонтальную плоскость, совпадающую с уровнем воды в резервуаре, т.е. с сечением I-I (см. рис. 5.10). Выбор именно этих сечений обусловлен тем, что для них известно наибольшее число слагаемых трехчлена

(z + p / ρ g + a u ² / 2g ).

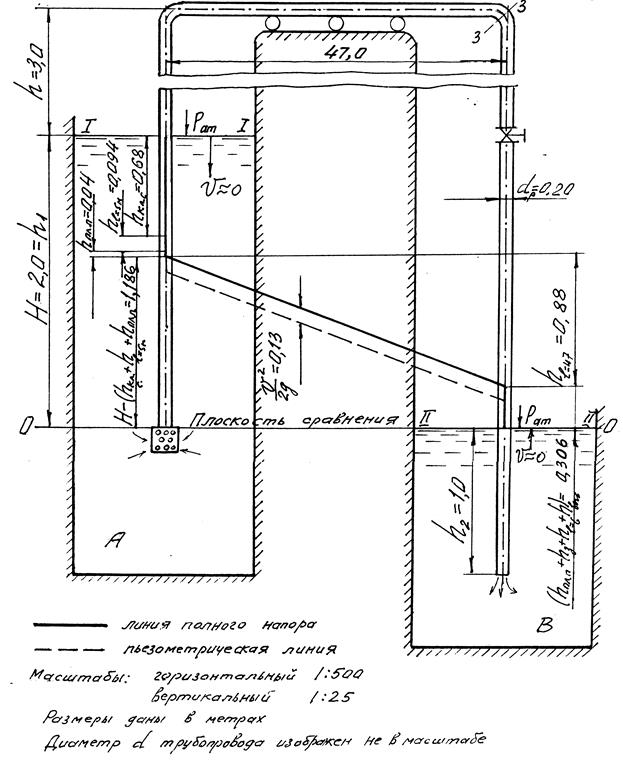
Рис. 5.9. График напоров (к задаче 5.3.4)

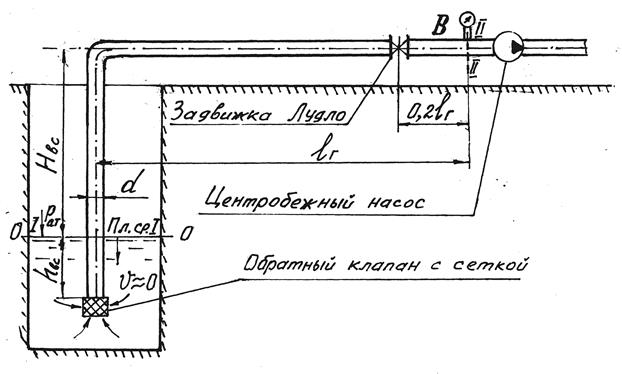
Рис. 5.10. Схема к гидравлическому расчету
всасывающего трубопровода насоса (к задаче 5.3.5)

Для выбранных сечений, плоскости сравнения и принятых обозначений слагаемые уравнения Д. Бернулли примут вид

z ₁ = 0; p _1изб / ρ g = 0; a ₁ u ₁ ² / 2 g » 0;

z ₂ = Н_вс; p _2изб / ρ g = –50∙10³ / 1000 ∙9,81; a ₂ u ₂ ² / 2 g = u ² / 2 g ;

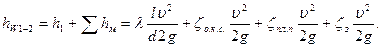
Разрешив уравнение Д. Бернулли относительно Н_вс, получим

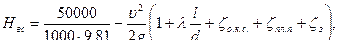(5.9)

где u = Q /ω = 4 Q /π d ² – средняя скорость потока воды в трубопроводе, м/с;

λ –коэффициент гидравлического трения;

ζ _о.к.с – коэффициент сопротивления обратного клапана с сеткой;

ζ _пл.п – коэффициент сопротивления плавного поворота;

ζ _з – коэффициент сопротивления задвижки Лудло при a / d = 0,5.

Как видим, задача по определению Н_вс сводится к определению потерь напора по длине и местных, а фактически – к нахождению коэффициентов гидравлического трения и местных сопротивлений.

Прежде всего выясним режим движения воды и область гидравлического сопротивления, в которой будет работать трубопровод.

С этой целью вычислим по уравнению (4.6) среднюю скорость потока:

u = 4 Q /π d ² = 0,018 ∙ 4 / 3,14 ∙ 0,15² = 1,02 (м/с), а затем число Рейнольдса по формуле (4.9), предварительно найдя в приложении 1 коэффициент кинематической вязкости воды v при t = 15 °C, v = l,15 ∙ 10 ^-6 (м²/c).

Re = u d / v = 1,02 ∙ 0,15 / 1,15 ∙ 10^-6 = 153000 / 1,15 = 13 3043.

Re > Re _к _p = 2320, следовательно, режим движения воды в трубопроводе турбулентный, поэтому для установления области гидравлического сопротивления необходимо вычислить относительную шероховатость трубопровода Δ_Э / d, приняв предварительно величину Δ_Э по таблице в приложении 4 (Δ_Э = 1,0 мм), Δ_Э / d = 1/ 150 = 0,0067.

Имея Re и Δ_Э / d, обращаемся к графику Г.А. Мурина
(см. приложение 5) и с его помощью устанавливаем, что трубопровод будет работать в области квадратичного сопротивления, где коэффициент λ= f(Δ_Э/ d), и может быть вычислен, например, по формуле (4.16)

λ = 0,11(Δ_Э / d )^0,25 = 0,11(1 / 50)^0,25 = 0,032.

Величины коэффициентов местных сопротивлений находим в приложении 6 (ζ_о.к.с= 6,5; ζ_пл.п.= 0,37; ζ_з = 5,3).

Подставив найденные и заданные величины в выражение (5.9), найдем высоту установки насоса Н_вс:

Н_вс = 5,10 – (1,02² / 2 ∙ 9,81) [1 + 0,032 (30 / 0,15 + 6,5 + 0,37 + 5,3)] =
= 5,10 – (0,053 + 0,34 + 0,34 + 0,02 + 0,28) = 5,10 – 1,03 = 3,97 (м).

Имея скоростной напор, потери напора по длине и в местных сопротивлениях, приступаем к построению графика напоров. Выбрав масштабы (горизонтальный 1:200 и вертикальный 1:20), вычерчиваем трубопровод и обозначаем на нем сечения I-I и II-II и плоскость сравнения 0-0,совпадающую с сечением I-I (рис. 5.11). Линию полного напора строим, последовательно вычитая потери напора, нарастающие вдоль потока, из начального напора Н_нач (заданного пьезометрическим уровнем в резервуаре). Величина этого напора равна нулю, т.е. пьезометрический уровень в данном случае совпадает с плоскостью сравнения. Пьезометрическую линию строим, вычитая скоростной напора из полного напора в выбранных сечениях трубопровода.

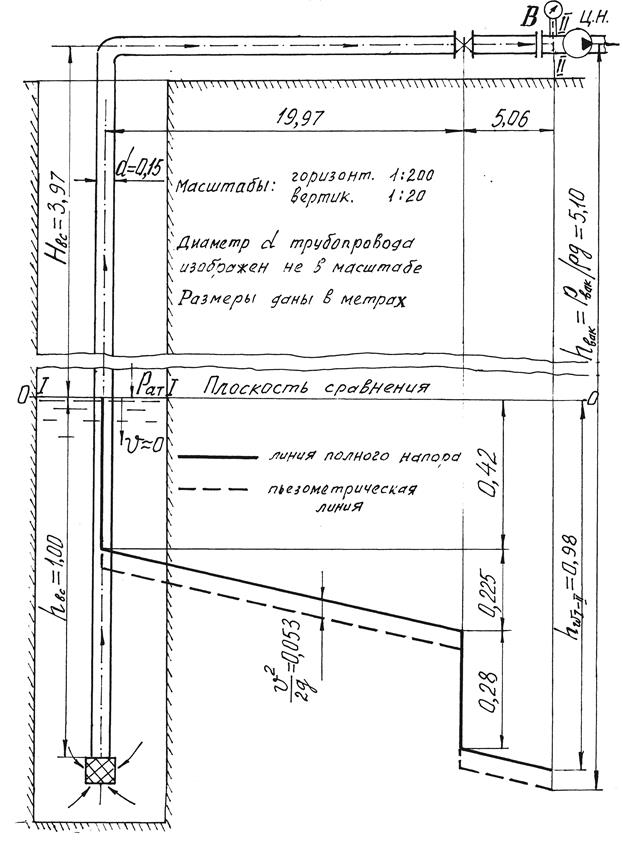
Рис. 5.11. График напоров (к задаче 5.3.5)

5.3. Задачи для самостоятельного решения

5.3.1 Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов (Рис.5.3.1.). Построить линии потенциальной и полной удельных энергий для данных табл. 5.3.1.

Температура воды tºС=20.

Рис. 5.3.1. К задаче 5.3.1.

Таблица 5.3.1.

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	10	20	30	40	50	60
l₁	м	100	120	80	60	50	45
l₂	м	200	150	130	110	90	80
l₃	м	150	100	90	80	70	60
d₁	мм	200	300	250	350	400	300
d₂	мм	300	200	200	300	350	300
d₃	мм	250	250	300	400	400	300
Δg	мм	0,50	1,05	0,50	0,75	1,15	1,0

5.3.2 .Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов (Рис.5.3.2.). При данных, указанных в таблице 5.3.2., построить линии потенциальной и полной удельных энергий. Температура воды Т,ºС=15.

Рис. 5.3.2. К задаче 5.3.2.

Таблица 5.3.2.

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	5	7,5	10	12,5	15	20
l₁	м	20	30	40	25	35	45
l₂	м	80	90	100	85	95	105
l₃	м	60	70	80	75	65	55
d₁	мм	125	150	100	125	150	150
d₂	мм	150	175	125	150	100	125
d₃	мм	125	150	75	100	125	150
Δg	мм	0,35	0,50	0,10	0,5	0,25	0,15

5.3.3.Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов (Рис.5.3.3.). Построить линии потенциальной и полной удельных энергий при данных, указанных в таблице 5.3.3.Температура воды Т,ºС=17.

Рис. 5.3.3. К задаче 5.3.3.

Таблица 5.3.3.

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	10	20	30	15	25	35
l₁	м	70	80	90	100	95	85
l₂	м	150	160	170	180	190	200
l₃	м	100	95	85	80	75	70
d₁	мм	200	250	300	250	400	125
d₂	мм	150	300	400	300	300	300
d₃	мм	125	125	250	225	250	250
Δ	мм	0,15	0,35	1,0	0,55	0,75	1,1

5.3.4. Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов, показанную на рис. 5.3.4. Построить линии потенциальной и полной удельных энергий при данных, указанных в таблице 5.3.4.

Температура воды Т,ºС=14.

Рис. 5.3.4. К задаче 5.3.4.

Таблица 5.3.4.

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	6	12	18	20	14	7
l₁	м	60	70	80	70	60	50
l₂	м	100	110	120	130	120	110
l₃	м	40	30	20	30	40	50
d₁	мм	100	125	200	200	200	250
d₂	мм	75	100	250	300	225	300
d₃	мм	100	150	175	250	150	150
Δ	мм	0,1	0,2	0,3	0,4	0,5	0,1

5.3.5.Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов (Рис. 5.3.5.). Высота выступа шероховатости Δ=1мм. Температура воды Т,ºС=13. На первой трубе установлен кран, степень закрытия которого характеризуется углом α=30º.

Построить линии потенциальной и полной удельных энергий.

Расчет провести при данных, указанных в табл. 5.3.5.

Рис. 5.3.5. К задаче 5.3.5.

Таблица 5.3.5

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	3	6	9	12	15	18
l₁	м	120	130	140	150	160	170
l₂	м	60	65	70	75	80	85
l₃	м	100	110	120	130	140	150
d₁	мм	50	50	100	150	150	300
d₂	мм	25	75	125	200	225	250
d₃	мм	75	25	75	175	150	225

5.3.6 Определить напор Н, необходимый для пропуска заданного расхода Q через систему коротких трубопроводов (Рис. 5.3.6). Построить линии потенциальной и полной удельных энергий при данных, указанных в таблице 5.3.6.

Температура воды Т,ºС=13.

Рис. 5.3.6. К задаче 5.3.6.

Таблица 5.3.6

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	20	25	30	35	25	20
l₁	м	120	125	130	135	140	130
l₂	м	80	90	95	100	105	100
l₃	м	60	65	70	75	80	85
d₁	мм	100	125	250	175	200	250
d₂	мм	200	150	200	250	225	300
d₃	мм	150	200	225	200	250	200
Δ	мм	0,15	0,25	0,5	1,00	0,75	0,10

5.3.7. Определить расход Q через заданную систему коротких трубопроводов, показанную на рис. 5.3.7. Построить линии потенциальной и полной удельных энергий. Расчет провести по данным, приведенным в табл. 5.3.7.

Рис. 5.3.7. К задаче 5.3.7.

Таблица 5.3.7.

Обозначения	Размерность	1	2	3	4	5	6
Н	м	30	28	26	24	22	20
l₁	м	200	190	180	170	160	150
l₂	м	160	140	130	120	110	100
l₃	м	90	85	80	75	70	65
d₁	мм	100	125	150	200	150	175
d₂	мм	125	150	125	100	100	250
d₃	мм	75	50	175	150	125	200

5.3.8. Определить расход Q через заданную систему коротких трубопроводов, показанную на рис. 5.3.8.

Построить линии потенциальной и полной удельных энергий, при данных, приведенных в табл. 5.3.8.

Рис. 5.3.8.. К задаче 5.3.8.

Таблица 5.3.8.

Обозначения	Размерность	1	2	3	4	5	6
Н	м	10	8	12	14	16	15
l₁	м	100	105	110	115	120	125
l₂	м	110	115	120	125	130	135
l₃	м	90	95	100	105	110	115
d₁	мм	150	200	300	250	200	250
d₂	мм	200	250	250	300	275	300
d₃	мм	175	300	275	225	225	200

5.3.9 Определить расход Q через заданную систему коротких трубопроводов (схема 5.3.9).

Построить линии потенциальной и полной удельных энергий, при данных, указанных в табл. 5.3.9.

Рис. 5.3.9. К задаче 5.3.9.

Таблица 5.3.9

Обозначения	Размерность	1	2	3	4	5	6
Н	м	15	17	21	25	24	22
l₁	м	100	110	120	130	130	125
l₂	м	90	95	105	115	135	120
l₃	м	60	80	90	95	105	90
d₁	мм	200	225	200	250	300	200
d₂	мм	250	250	250	300	225	225
d₃	мм	225	200	225	225	250	250

5.3.10. Определить расход Q через заданную систему коротких трубопроводов (рис. 5.3.10.).

Построить линии потенциальной и полной удельных энергий, при данных, указанных в табл. 5.3.10..

Рис. . 5.3.10.. К задаче . 5.3.10..

Таблица . 5.3.10.

Обозначения	Размерность	1	2	3	4	5	6
Н	м	20	25	30	35	27	21
l₁	м	100	110	120	130	140	150
l₂	м	150	160	170	180	190	200
l₃	м	70	80	90	100	110	120
d₁	мм	250	300	250	300	150	250
d₂	мм	200	275	200	250	250	300
d₃	мм	225	350	225	275	175	225

5.3.11. Определить расход Q через заданную систему коротких трубопроводов (рис . 5.3.11.).

При данных, приведенных в табл. . 5.3.11., построить линии потенциальной и полной удельных энергий.

Рис. . 5.3.11.. К задаче . 5.3.11.

Таблица . 5.3.11.

Обозначения	Размерность	1	2	3	4	5	6	7
Н	м	12	15	17	21	23	25	29
l₁	м	50	60	70	75	80	85	90
l₂	м	80	90	95	100	105	110	115
l₃	м	105	110	115	120	130	140	145
d₁	мм	250	250	300	300	200	225	150
d₂	мм	300	275	250	200	250	250	200
d₃	мм	225	200	275	250	300	200	225

5.3.12. Определить расход Q через заданную систему коротких трубопроводов (схема 5.3.12.).

Построить линии потенциальной и полной удельных энергий согласно данным, указанным в табл. 5.3.12.

Рис. . 5.3.12. К задаче . 5.3.12.

Таблица 5.3.12.

Обозначения	Размерность	1	2	3	4	5	6
Н	м	15	18	20	22	24	26
l₁	м	50	55	60	65	70	75
l₂	м	100	110	120	130	140	150
l₃	м	50	55	60	65	70	75
d₁	мм	100	300	250	200	175	150
d₂	мм	75	250	200	250	250	200
d₃	мм	125	275	225	225	200	150

5.3.12.Определить напор Н над центром выходного отверстия для пропуска заданного расхода Q через систему коротких водопроводов и

построить линию полной удельной энергии и пьезометрическую линию.

Расчет выполнить при данных, приведенных в табл. 5.3.12.при расположении труб, как на рис. 5.3.12. Трубы нормальные, высота шероховатости стенок Δ=1,35 мм. Температура воды ТºС.

Рис. . 5.3.12. К задаче . 5.3.12.

Таблица 5.3.12.

№ п/п	Q, л/сек	d₁, мм	d₂, мм	l, м	z, м	Тº
1	4	50	75	40	0,6	10
2	9	75	100	80	0,8	12
3	15	125	100	100	1,0	15
4	12	100	125	140	1,2	20
5	35	150	200	150	1,2	15
6	50	200	150	80	1,0	10

5.3.13.Определить напор Н, необходимый для пропуска заданного расхода через систему коротких водопроводов и построить линию полной удельной энергии и пьезометрическую линию при расположении труб, как на схеме 5.3.13. Вычислить удельную потенциальную энергию в обоих случаях для сечений b-b и c-c. Трубы чугунные новые (Δ≈0,5мм), высота шероховатости стенок Δ=1,35 мм. Температура воды ТºС.

Расчет выполнить при данных, приведенных в табл. 5.3.13.

Рис. . 5.3.13. К задаче . 5.3.13.

Таблица 5.3.13.

№ п/п	Q, л/сек	d₁, мм	d₂, мм	l, м	Тº
1	8	50	75	8	20
2	9	75	50	14	15
3	10	75	50	12	12
4	11	50	75	8	10
5	8	100	75	40	20
6	9	50	100	20	20

5.3.14 .Определить диаметр d₂ на втором участке водопровода, который при заданных значениях d₁, l₁, l₂, h₁ и z пропустит расход Q (рис. 5.3.14 .). Трубы гидравлически шероховатые, высота выступов шероховатости стенок труб Δ=1,35мм (n=0,012). Температура воды Т=10ºС. Построить линию полной удельной энергии и пьезометрическую линию (при принятом диаметре d₂). Расчет выполнить при данных, приведенных в табл. 5.3.14 .

Рис. . 5.3.14 .. К задаче . 5.3.14 .

Таблица 5.3.14 .

№ п/п	d₁, мм	l₁, м	l₂, м	h₁, м	z, м	Q, л/сек
1	75	20	11	4,0	1,0	4
2	50	10	73	7,4	1,4	6
3	100	67	20	5,0	1,5	8
4	75	20	90	5,7	1,7	10
5	125	50	50	6,7	1,7	15
6	100	39	80	8,5	2,0	20

5.3.15 .Определить скорость истечения и расход воды при заданных значениях h, z, l₁, l₂ (схема 5.3.15) и диаметре трубы d. Трубы нормальные. Высота выступов шероховатости Δ≈1,35мм. Температура воды Т=20ºС. Угол открытия крана α. Построить линию полной удельной энергии и пьезометрическую линию. Расчет выполнить при данных, приведенных в табл. 5.3.15

Рис. . 5.3.15.. К задаче . 5.3.15 .

Таблица 5.3.15

№ п/п	d, мм	h, м	z, м	l₁, м	l₂, м	αº
1	75	7,0	2,0	30	10	20
2	100	7,0	1,0	40	20	30
3	125	5,8	1,2	20	50	30
4	150	4,5	1,5	70	10	20
5	200	3,3	1,7	80	20	30
6	250	3,0	1,0	30	70	40

5.3.16 Определить расход Q через систему коротких водопроводов при заданных напоре, диаметрах и длине труб. Построить линию полной удельной энергии и пьезометрическую линию.

Расчет выполнить при данных, приведенных в табл. 5.3.16.

Трубы нормальные, высота выступов шероховатости стенок Δ=1,35мм. Температура воды ТºС.

Рис. . 5.3.16.. К задаче . 5.3.16 .

Таблица 5.3.16

№ п/п	Н, м	d₁, м	d₂, м	l, м	ТºС
1	7	75	50	60	20
2	6	75	100	80	15
3	5	125	100	100	12
4	4	125	150	80	10
5	3	200	150	50	10
6	2	200	250	40	12

5.3.17. Определить напор Н. необходимый для подачи расхода Q через систему коротких трубопроводов (рис. 5.3.17).

Высота выступа шероховатости Δ=1,35 мм.

Температура воды ТºС=15.

На второй трубе установлен кран, степень закрытия которого характеризуется углом αº.

Построить линии потенциальной и полной удельных энергий. Расчет выполнить при данных, приведенных в табл. 5.3.17.

Рис. . 5.3.17.. К задаче . 5.3.17 .

Таблица 5.3.17

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	17	23	29	35	41	44
d₁	мм	100	125	200	150	175	250
d₂	мм	125	150	250	225	250	200
d₃	мм	75	100	175	200	225	225
d₄	мм	100	150	200	175	200	200
l₁	м	60	65	70	75	80	85
l₂	м	100	110	120	130	140	150
l₃	м	40	50	60	65	70	75
l₄	м	30	25	40	42	53	38
l₅	м	20	25	30	40	50	60
α₁º	град	30	30	40	45	45	60
α₂º	град	135	30	150	120	120	165
α₃º	град	10	150	20	20	30	30

5.3.18.Определить величину давления p, необходимого для подачи расхода Q через систему коротких трубопроводов (схема 5.3.18). Отметки горизонтов воды в обоих резервуарах постоянны. Высота выступа шероховатости Δ=1,35 мм. Степень закрытия задвижки, установленной на 4-й трубе, характеризуется отношением а/d. Построить линии потенциальной и полной удельных энергий.

Расчет провести при данных, приведенных в табл. 5.3.18

Рис. . 5.3.18.. К задаче . 5.3.18 .

Таблица 5.3.18

Обозначения	Размерность	1	2	3	4	5	6
Q	л/сек	19	23	28	33	42	47
d₁	мм	100	150	200	200	250	250
d₂	мм	125	100	150	225	300	275
d₃	мм	75	125	175	200	200	250
d₄	мм	100	100	150	250	225	225
l₁	м	30	35	42	44	47	51
l₂	м	59	64	71	80	87	95
l₃	м	25	31	38	56	39	71
l₄	м	100	108	110	114	117	120
l₅	м	50	40	35	40	30	20
α₁º	град	30	40	50	60	30	30
α₂º	град	120	130	140	150	120	130
α₃º	град	130	140	120	140	130	120
а/d		1/4	3/8	½	5/8	½	3/8
h	м	3	4	5	5,5	4,8	5,3
T	ºС	20	15	14	13	17	15

Дата: 2019-11-01, просмотров: 812.

⇐ Предыдущая 1 234 5 6 Следующая ⇒