При рассмотрении силового воздействия покоящейся жидкости на ограничивающие ее поверхности обычно интересуются равнодействующей силой Р избыточного гидростатического давления. Величину этой силы, действующей на плоскую поверхность произвольной формы площадью ω и наклоненной под углом a к горизонту (рис. 2.1 и 2.2), вычисляют по любой из трех приведенных ниже формул:
Р = рСизбω, (2.1)
где рСизб – избыточное гидростатическое давление в центре тяжести С площади ω;
ω – площадь плоской поверхности, смачиваемая жидкостью.
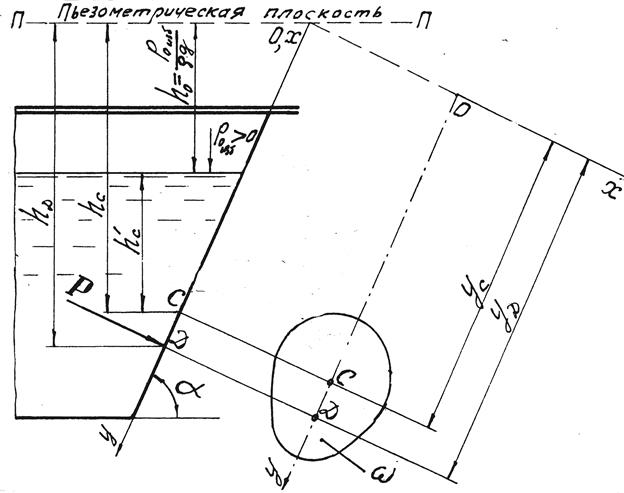
Рис. 2.1. К определению равнодействующей силы Р
избыточного гидростатического давления на плоскую поверхность
Подставив в формулу (2.1) вместо рСизб его выражение из основного уравнения гидростатики (1.2), получим вторую формулу для вычисления силы гидростатического давления
Р = (р0изб + ρgh ¢ с )ω, (2.2)
где р0изб – внешнее избыточное давление;
ρgh' c – весовое давление;
h ¢ c – заглубление центра тяжести С площади ω под уровень свободной поверхности жидкости.
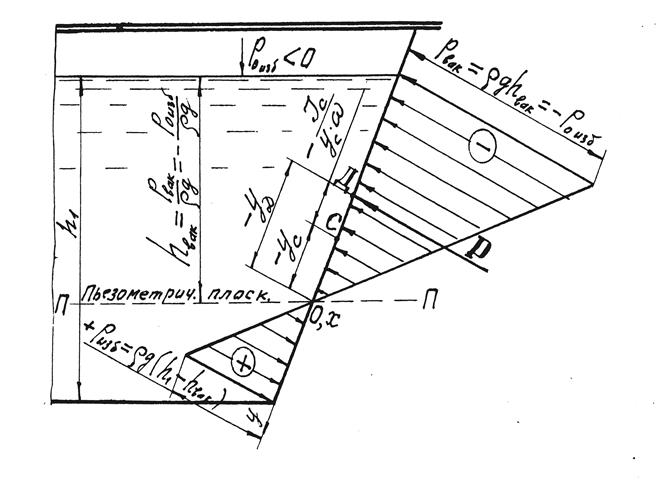
Рис. 2.2. К определению положения центра давления Д, когда
в центре тяжести С отрицательное избыточное гидростатическое давление
Выразив р0изб, входящее в формулу (2.2), через пьезометрическую высоту hР0изб (см. рис.2.1 и 2.2), получим третью формулу для определения силы Р гидростатического давления:
Р = ρg(hР0изб + h¢c) = ρghсω, (2.3)
где hc – расстояние по вертикали от центра тяжести С площади ω до пьезометрической плоскости (см. рис. 2.1).
Сила Р приложена в точке Д, называемой центром давления (см. рис. 2.1 и 2.2). Координату уД центра давления, т.е. расстояние, измеряемое по стенке от оси ОХ до точки Д, вычислим по формуле
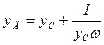
, (2.4)
где у C – расстояние, измеряемое по стенке от оси ОХ до центра тяжести С площади ω;
IC – центральный момент инерции площади ω, т.е. момент инерции относительно горизонтальной оси, проходящей через центр тяжести С площади ω;
у C ω – статический момент площади ω относительно оси ОХ.
При рСизб > 0 центр давления Д лежит ниже центра тяжести С площади ω(см. рис. 2.1 и 2.2). Если же рСизб <0, центр давления Д располагается выше центра тяжести С (см. рис. 2.2). При этом сила Р действует в противоположном, по сравнению с показанным на рис. 2.1, направлении.
Если плоская стенка, на которую оказывает давление жидкость, прямоугольная, силу давления на нее жидкости можно определить графоаналитическим методом, основанным на использовании эпюры гидростатического давления.
На рис. 2.3 дан пример определения силы Р избыточного
гидростатического давления графоаналитическим методом на плоский щит, закрывающий прямоугольное отверстие высотой а и шириной b . В данном случае эпюра гидростатического давления на щит представляет собой трапецию высотой а с основаниями ρgh 1 и ρgh 2 .
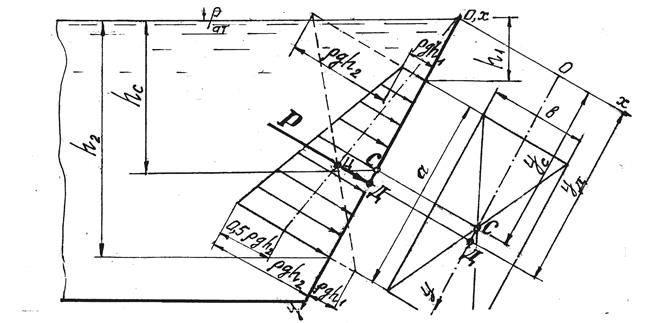
Рис. 2.3. К определению равнодействующей силы Р
избыточного гидростатического давления
на плоскую прямоугольную стенку графоаналитически
Площадь эпюры
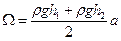
численно равна силе избыточного давления жидкости на единицу ширины щита. Следовательно, на весь щит шириной b действует сила
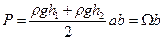. (2.5)
Справедливость формулы (2.5) доказывается тем, что в ней
(h 1 + h 2 ) / 2 = hC , ab = ω, после чего эта формула становится идентичной формуле (2.3).
Линия действия силы Р проходит через центр тяжести Ц площади эпюры Ω перпендикулярно к плоскости щита (см. рис. 2.3). Точка встречи линии действия силы Р со щитом является центром давления Д. Координату уД центра давления при графоаналитическом методе решения
задачи определяют по чертежу стенки, измеряя отрезок ОД (см. рис. 2.3) и умножая его длину на масштаб.
Примеры решения задач
Задача 2.2.1. Определить величину силы Р давления воды на прямоугольный щит, наклонённый под углом a = 60° к горизонту, и координату уД центра давления Д (рис. 2.4). Глубина воды перед щитом
h = 2,0 м, ширина щита b = 1,4 м. Решить задачу аналитическим и графоаналитическим методами.
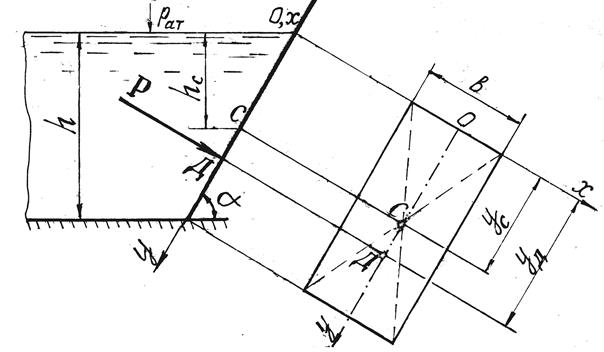
Рис. 2.4. Расчетная схема к определению силы Р давления воды
на прямоугольный плоский щит (к задаче 2.2.1)
Аналитическое решение. Величину силы Р вычислим по формуле (2.3). Для условий настоящей задачи h С = h /2, ω= hb / sin a , поэтому формула (2.3) принимает вид
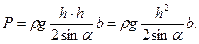
Подставив в это выражение числовые значения величин, найдем силу давления воды на щит:
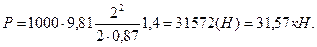
Координату уД центра давления Д вычислим по формуле (2.4). Величины, входящие в эту формулу, для условий нашей задачи выражаются следующим образом:
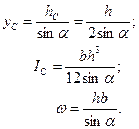
Записав формулу (2.4) с учетом выражений для уС, IС, ω и подставив числовые значения величин, получим:
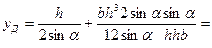
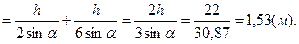
Графоаналитическое решение. В основе решения задачи названным методом лежит использование эпюры гидростатического давления, построенной на прямоугольный щит.
Величину силы Р найдем через площадь Ω эпюры гидростатического давления по формуле (2.5).
Для построения эпюры предварительно найдем гидростатическое давление в нижней точке щита, т.е. на глубине h = 2,0 м, и на свободной поверхности воды, т.е. при h = 0,00 м, и примем масштабы: для расстояний – 1:25, для давлений в 1 см – 5 кПа. Построенная эпюра представляет собой прямоугольный треугольник (рис. 2.5)
Вычислим площадь эпюры гидростатического давления воды на щит:
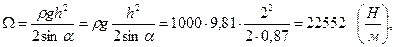
а затем и силу Р давления воды на весь щит, умножив площадь Ω на ширину щита b :
P = Ωb = 22552 ∙ 1,40 = 31572 ( H ) = 31,57 кН.
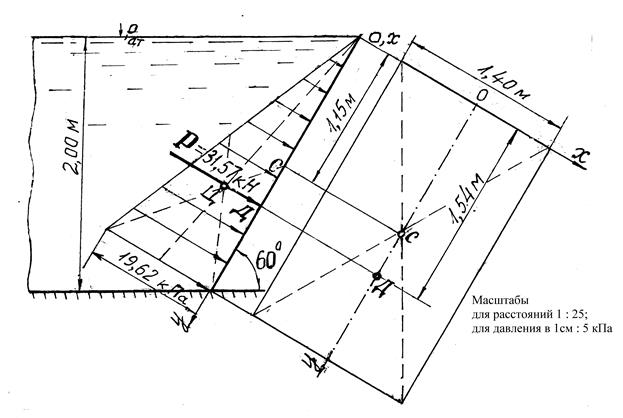
Рис. 2.5. Определение силы давления воды Р и координаты
центра давления Д на прямоугольный щит
графоаналитическим методом (к задаче 2.2.1)
Для нахождения центра давления Д и его координаты уД определим графически центр тяжести Ц площади Ω эпюры гидростатического давления (в нашем случае точка Ц находится на пересечении медиан треугольника). Проводим через точку Ц перпендикуляр к щиту и в точке его встречи со щитом получаем центр давления Д. Измерив по стенке расстояние от оси ОХ до точки Д и умножив его на масштаб, находим координату центра давления уД = 1,54 м (см. рис. 2.5).
Сравнивая величины Р и уД, полученные аналитическим и графоаналитическим методами, видим, что значения силы Р оказались одинаковыми, а относительное расхождение значений уД равно:
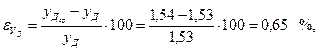
что значительно меньше предельного, равного 5 %.
Задача 2.2.2. Определить результирующую силу Р давления воды на наклонный прямоугольный затвор (рис. 2.6) и координату уД центра давления аналитическим и графоаналитическим методами. Ширина затвора b – 4,0 м, глубина воды перед затвором h1 = 3,0 м, за ним h2=1,0 м. Угол наклона затвора к горизонту a = 60°. Затвор может вращаться вокруг
горизонтальной оси. Превышение оси вращения над уровнем воды перед затвором a = 0,6 м.
Определить также силу Т, необходимую для подъема щита, пренебрегая его весом и трением.
Решение. Результирующая сила Р давления воды на затвор равна алгебраической сумме сил Р1 и Р2 давления воды на затвор слева и справа, т.е. Р = P 1 – P 2, поэтому прежде всего определим силы Р1 и Р2 и координаты уД1 и уД2 центров их давления. Имея силы Р1, Р2, Р и координаты уД1 и уД2, можно, составив уравнение моментов сил относительно оси вращения затвора, найти координату уД центра давления силы Р.
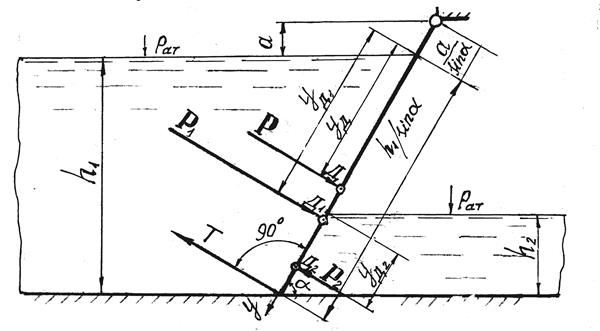
Рис. 2.6. Схема к определению силы Р давления воды
на прямоугольный затвор (к задаче 2.2.2)
Аналитическое решение. Воспользовавшись формулами (2.3) и (2.4), вычислим предварительно Р1 и Р2, а также уД1 и уД2.
.
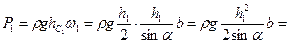
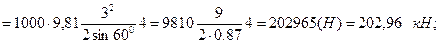
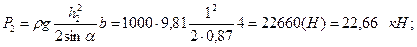
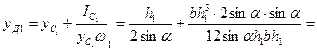
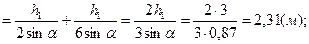
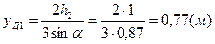Найдем силу Р давления воды на затвор как разность сил Р1 и Р2, поскольку направления их действия противоположны.
Р=Р1 – Р2 = 202,96 – 22,66 = 180,30 (кН).
Найдем силу Т, для чего составим уравнение моментов сил Р1, Р2 и Т относительно оси вращения затвора:
откуда
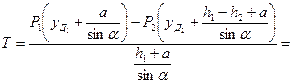
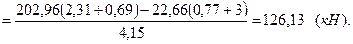
Для нахождения величины уД составим уравнение моментов сил Р и Т относительно оси вращения затвора:
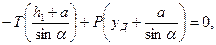
откуда
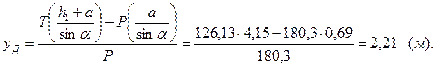
Графоаналитическое решение. Построим в масштабе эпюры гидростатического давления на затвор слева и справа (рис. 2.7).
Разность площадей этих эпюр (площадь трапеции ABKL ), умноженная на ширину b затвора, численно равна искомой силе Р, т.е.
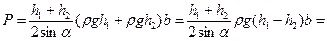
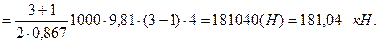
Для нахождения положения центра давления (точка Д) определим центр тяжести Ц трапеции ABKL и проведем через него перпендикуляр к плоскости затвора. Точка пересечения перпендикуляра с затвором будет центром давления Д. Измерив отрезок АД (см. рис. 2.7) и умножив его на масштаб, получим координату уД =2,20 м.
Сравнивая величины Р и уД, полученные аналитическим и графоаналитическим методами, находим, что разница между ними составляет соответственно 0,4 % и 0,5 %, т.е. значительно меньше предельной допустимой погрешности, равной 5 %. Одновременно мы убедились, что графоаналитическое решение задачи проще и нагляднее аналитического.
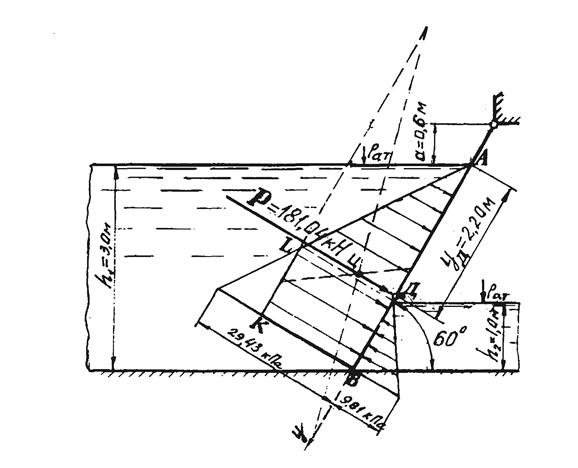
Рис. 2.7. К определению равнодействующей силы Р давления воды
на прямоугольный затвор графоаналитическим методом (к задаче 2.2.2)
Задача 2.2.3. Цилиндрическая цистерна диаметром d = 2,4 м (рис. 2.8) заполнена бензином до верха горловины (высота последней h Г = 0,6 м ). Плотность бензина ρб = 740 кг/м3.
Определить силу давления бензина Р на торцевую плоскую стенку цистерны и координату h Д точки ее приложения.
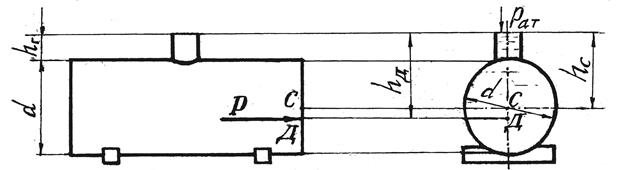
Рис. 2.8. Схема к определению силы Р давления бензина
на плоскую торцевую стенку цистерны (к задаче 2.2.3)
Решение. Силу Р давления бензина вычислим по формуле (2.3), которую для условий задачи запишем в виде
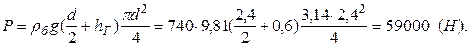
Координату h Д центра давления Д (точки приложения силы Р) вычислим по формуле (2.4), записанной для условий данной задачи. После подстановки в нее числовых значений величин получим:
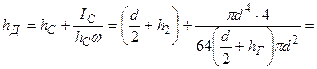
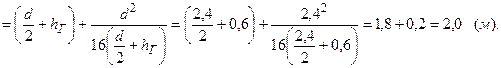
Задача 2.2.4. Поворотный клапан АВ закрывает выход из бензохранилища в трубу квадратного сечения со стороной h = 0,3 м
(рис. 2.9). Прямоугольная пластина клапана АВ опирается на срез трубы, выполненный под углом a = 45°. В трубе бензин отсутствует. Определить силу натяжения троса Т, необходимую для открывания клапана (без учета его веса и трения в шарнире А и в ролике К), если превышение уровня бензина над нижней точкой В клапана составляет Н = 0,85 м, а давление на свободной поверхности бензина, показываемое манометром М, равно
рман = 5 кПа. Плотность бензина рб = 700 кг/м3.
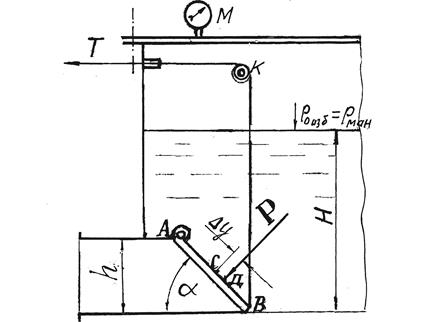
Рис. 2.9. Расчетная схема к определению силы давления бензина
на плоский прямоугольный клапан АВ (к задаче 2.2.4)
Решение. Очевидно, что сила давления бензина Р на клапан АВ, приложенная в центре давления Д, будет препятствовать открыванию клапана.
Силу натяжения троса Т найдем из уравнения моментов сил относительно шарнира А:
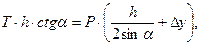
где h ctg a – плечо силы Т относительно шарнира А;
Р = рсω = ρб ghcω = ρб g ( p ман / ρб g + H – 0,5) h 2 / sin a – сила давления бензина на клапан (см. формулу 2.3 и рис.2.1);
Δу = IC / yC ω – смещение центра давления относительно центра тяжести С клапана (см. формулу 2.4 и рис. 2.1);
( h /2 sin a )+Δ y – плечо силы Р относительно шарнира A.
Для условий данной задачи центральный момент инерции IC смоченной площади ω клапана АВ и координата у C центра тяжести С соответственно равны:
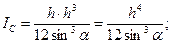
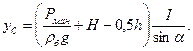
Определим величины Р и Δу, входящие в уравнение моментов сил:
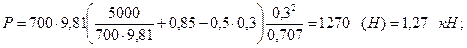
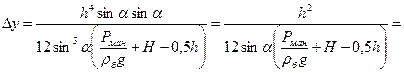
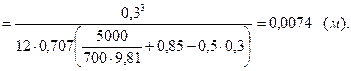
Вычислим силу Т натяжения троса:
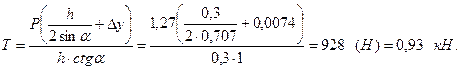
Задача 2.2.5. Канал прямоугольного сечения шириной b = 2 м перегорожен вертикальным плоским щитом (рис. 2.10). Глубина воды перед щитом h = 3,0 м. Вес щита G = 20 кН. Коэффициент трения в пазах канала при подъеме щита f = 0,25. Определить силу Р давления воды на щит и координату h Д центра давления аналитическим и графоаналитическим методами, а также усилие Т, которое нужно приложить для подъема щита.
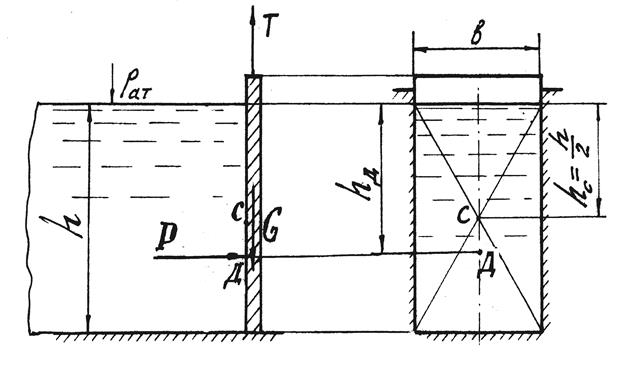
Рис. 2.10. Схема к определению силы давления воды
на прямоугольный вертикальный щит (к задаче 2.2.5)
Решение. Определим величины Р и h Д аналитическим методом. Для этого воспользуемся формулами (2.3) и (2.4) и получим.
P =9,8 ∙1000 ∙ (3/2) ∙(3∙2)=88,2кН.
h Д =1,5+(2∙33 ∙2/12∙3∙2∙3)=1,5+(3/6)=2,0(м)
Для определения величин Р и hД графоаналитическим методом построим эпюру избыточного гидростатического давления на щит
(рис. 2.11). В данном случае эпюра представляет собой прямоугольный треугольник ОАВ с основанием ρgh =1000 ∙ 9,81 ∙ 3,0 = 29430 Па =29,43кПа и высотой h = 3,0 м. Площадь этой эпюры Ω = ρgh2 / 2 численно равна силе давления воды, приходящейся на единицу ширины щита, т.е.
Ω = 29,43 (кПа) · 1,5 (м) = 44,145 кПа/м = 44,145 кН/м.
Сила давления воды на весь щит шириной b = 2,0 м равна объему эпюры гидростатического давления Р = Ω b , т.е.
Р=44,145 (кН/м) ∙ 2,0 (м) = 88,29 кН.
Для нахождения центра давления Д сначала определим графически центр тяжести Ц эпюры гидростатического давления (он находится в точке пересечения медиан треугольника ОАВ), т.е. на глубине 2/3 h . Затем через точку Ц проводим перпендикуляр к плоскости щита. Линия действия силы Р совпадает с этим перпендикуляром, а точка его встречи с плоскостью шита дает центр давления Д координата которого
h Д = (2/3) h = (2/3)∙3 = 2 (м).
Сравнивая величины h Д и Р, полученные аналитическим и графоаналитическим методами, видим, что они одинаковы.
Усилие Т, необходимое для подъема щита, вычислим по формуле, известной из курса физики:
T = G + fP = 20 + 0,25 ∙ 88,29 = 20 + 22,07 = 42,07 (кН).
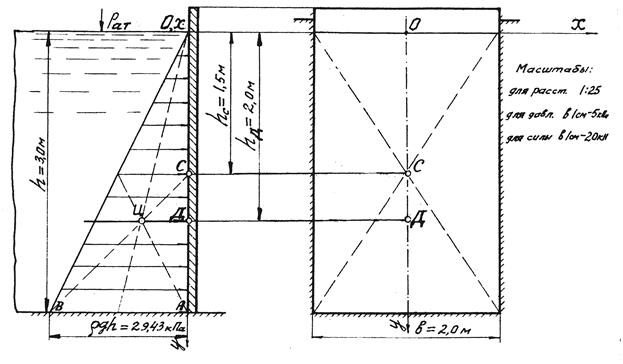
Рис. 2.11. К определению силы давления воды
на прямоугольный вертикальный щит графоаналитическим методом
(к задаче 2.2.5)
2.3 Задачи для самостоятельного решения
2.3.1 Определить силы манометрического давления воды на грани АВ, ВС и СЕ устоя (рис 2.3.1.), а также центры давления этих сил. Расчет выполнить аналитическим и графоаналитическим способами. Глубина воды перед устоем h; высота грани АВ – h1, высота грани СЕ – h3, угол наклона грани ВС к горизонту α. Ширина устоя b.
Расчет выполнить при данных, приведенных в табл. 2.3.1.
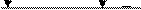
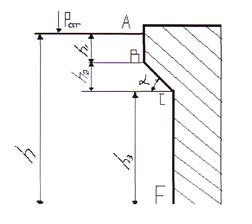
Рис. 2.3. 1 . К задаче 2.3.1
Таблица 2.3. 1 .
| № п/п | h1, м | h2, м | h3, м | b, м |
| 1 | 0,8 | 0,5 | 1,8 | 5 |
| 2 | 1,0 | 1,5 | 2,0 | 6 |
| 3 | 1,8 | 0,8 | 3,8 | 7 |
| 4 | 1,5 | 2,5 | 2,6 | 8 |
| 5 | 2,3 | 3,5 | 2,8 | 9 |
| 6 | 1,2 | 1,5 | 3,4 | 7 |
2.3.2 Определить коэффициенты устойчивости стенки (рис. 2.3.2) на сдвиг и опрокидывание. Плотность кладки ρкл, коэффициент трения стенки по основанию ƒ. Построить эпюры весового давления воды на вертикальные и горизонтальные грани стенки.
Указание. Расчет выполнить на 1 пог. м длины стенки, аналитическим и графоаналитическим способами, при данных, приведенных в табл. 2.3.2.
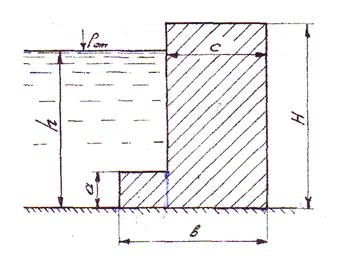
Рис. 2. 3. 2 К задаче 2.3.2
Таблица 2.3. 2
| № п/п | Н, м | h, м | b, м | c, м | a, м | ρкл, кг/ м3 | ƒ |
| 1 | 6,0 | 4,5 | 3,5 | 2,6 | 0,8 | 2200 | 0,3 |
| 2 | 5,5 | 5,0 | 3,8 | 2,5 | 1,0 | 2300 | 0,34 |
| 3 | 6,5 | 5,3 | 4,5 | 2,6 | 0,8 | 2400 | 0,35 |
| 4 | 7,5 | 5,5 | 4,8 | 2,5 | 1,0 | 2400 | 0,38 |
| 5 | 7,0 | 6,5 | 5,5 | 2,6 | 0,8 | 2500 | 0,39 |
| 6 | 8,5 | 7,5 | 5,8 | 2,5 | 1,0 | 2300 | 0,3 |
2.3.3 Прямоугольный вертикальный щит, перегораживающий прямоугольный канал шириной b, находится в пазах (рис. 2.3.3.). Вес щита G, коэффициент трения в пазах ƒ=0,5. Глубина воды перед щитом h1, за щитом h2.
Определить усилие Т, необходимое для поднятия щита.
Указание. Расчет выполнить аналитическим и графоаналитическим способами, при данных, приведенных в табл. 2.3.3.
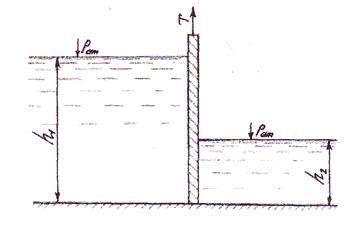
Рис. 2.3. 3 К задаче 2.3.3
Таблица 2.3. 3
| № п/п | b, м | G, кН | h1, м | h2, м |
| 1 | 4,0 | 4,9 | 3,0 | 1,0 |
| 2 | 3,0 | 3,7 | 3,0 | 1,5 |
| 3 | 5,0 | 5,9 | 4,0 | 2,0 |
| 4 | 6,0 | 5,7 | 4,0 | 2,5 |
| 5 | 7,0 | 4,2 | 5,0 | 3,0 |
| 6 | 8,0 | 4,7 | 5,0 | 3,5 |
2.3.4 Определить горизонтальную и вертикальную составляющие силы давления воды на 1 пог. м подпорной стенки (рис. 2.3.4).
Указание. Горизонтальную составляющую силы давления воды определить аналитическим и графоаналитическим методами, вертикальную – только аналитическим методом.
Расчет выполнить при данных, приведенных в табл. 2.3.4.
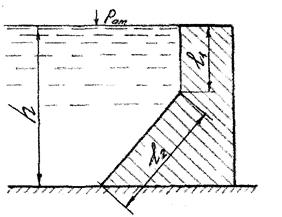
Рис. 2.3. 4 . К задаче 2.3.4
Таблица 2.3. 4 .
| № п/п | b, м | l1, м | l2, м | h, м |
| 1 | 3,0 | 1,0 | 2,2 | 2,0 |
| 2 | 2,0 | 2,0 | 3,2 | 4,2 |
| 3 | 4,0 | 2,5 | 4,2 | 5,2 |
| 4 | 5,0 | 1,5 | 3,8 | 4,8 |
| 5 | 5,5 | 1,8 | 3,2 | 3,2 |
| 6 | 6,0 | 3,0 | 4,0 | 6,0 |
2.3.5 Определить усилия T1 и Т2, необходимые для открывания прямоугольного вертикального затвора высотой а и шириной b при заглублении верхней точки затвора под уровень воды на величину h (рис. 2.3.5) для двух вариантов расположения шарнира А (в нижней и верхней точках затвора).
Указание. Момент силы тяжести затвора и трение в шарнире не учитывать. Расчет выполнить аналитическим и графоаналитическим способами, при данных, приведенных в табл. 2.3.5.
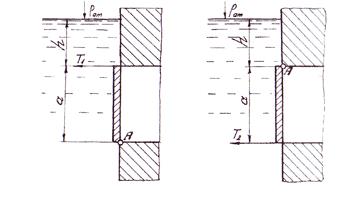
Рис. 2.3. 5 Схема к определению силы давления воды на прямоугольный затвор (к задаче 2.3.5)
Таблица 2.3. 5
| № п/п | a, м | b, м | h, м |
| 1 | 1,0 | 2,0 | 0,5 |
| 2 | 1,8 | 1,0 | 2,0 |
| 3 | 0,5 | 1,0 | 2,0 |
| 4 | 2,0 | 1,8 | 1,0 |
| 5 | 2,0 | 0,5 | 1,0 |
| 6 | 1,0 | 2,0 | 1,8 |
2.3.6. Определить силу давления воды на щит и центр давления. Щит прямоугольного сечения шириной b наклонен под углом α к горизонту. Глубина воды перед щитом h 1 за щитом h 2 (Рис.2.3.6).
Расчет выполнить аналитическим способом и проверить графоаналитически. Вычислить начальное подъемное усилие, если коэффициент трения f = 0,5, а относительный вес материала щита
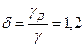. Толщина щита е. Превышение (по вертикали) верхней кромки щита над горизонтом перед щитом а Расчет выполнить при данных, приведенных в табл. 2.3.6..
Указание. Относительный вес — это отношение удельного веса тела ( γg ) к удельному весу воды (γ)
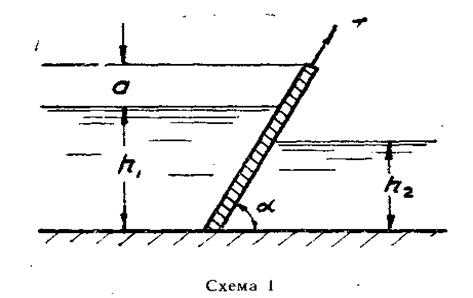
Рис.2.3.6. К задаче 2.3.6.
Таблица 2.3.6.
| № п/п | h1 , м | h2, м | b, м | α | a,м | е, м |
| 1 | 0,9 | 0,5 | 1,0 | 45 | 0,2 | 0,06 |
| 2 | 1,2 | 0,6 | 1,2 | 60 | 0,3 | 0,06 |
| 3 | 1,5 | 0,8 | 1,4 | 90 | 0,3 | 0,06 |
| 4 | 1,8 | 0,9 | 1,6 | 45 | 0,4 | 0,08 |
| 5 | 2,1 | 1,0 | 1,8 | 60 | 0,4 | 0,08 |
| 6 | 2,4 | 1,0 | 2,0 | 90 | 0.5 | 0,08 |
2.3.7 Перед клапанным затвором, имеющим плоскую поверхность размером lхb, глубина воды Н (рис. 2.3.7.). Определить силу натяжения троса Т, удерживающего затвор в заданном положении (без учета трения в опоре). Гидравлическую часть задачи решить аналитическим и графоаналитическим методами.
Расчет выполнить при данных, приведенных в табл. 2.3.7.
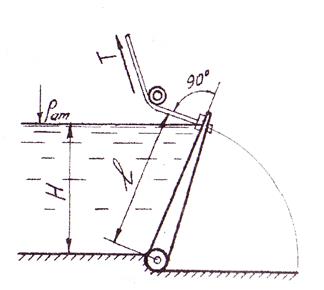
Рис. 2.3. 6 К задаче 2.3.7
Таблица 2.3. 6
| № п/п | l, м | b, м | H, м |
| 1 | 2,5 | 10,0 | 2,3 |
| 2 | 3,0 | 6,0 | 2,4 |
| 3 | 2,3 | 2,3 | 1,9 |
| 4 | 2,4 | 2,4 | 2,1 |
| 5 | 3,4 | 3,0 | 3 |
| 6 | 2,8 | 2,3 | 2,5 |
2.3.8 Резервуар с нефтью (ρH=920 кг/м3) разделен на две части перегородкой, имеющей квадратное отверстие со стороной a (рис. 2.3.8). Гидростатическое давление над нефтью в левой части резервуара, измеряемое пружинным манометром М составляет Pманн, а в правой – измеряемое вакуумметром В – Pвак. Определить величину результирующей силы гидростатического давления на крышку, закрывающую отверстие, и координату точки приложения силы .
Указание. Расчет выполнить аналитическим и графоаналитическим способами, при данных, приведенных в табл. 2.3.8.
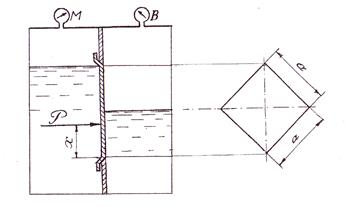
Рис. 2.3. 7 Схема к определению силы давления нефти на плоскую вертикальную квадратную крышку (к задаче 2.3.8)
Таблица 2.3. 7
| № п/п | a, м | Pманн, кПа | Pвак, кПа |
| 1 | 1,0 | 15 | 10 |
| 2 | 1,5 | 25 | 30 |
| 3 | 2,0 | 35 | 20 |
| 4 | 3,5 | 45 | 15 |
| 5 | 4,0 | 55 | 25 |
| 6 | 5,0 | 65 | 35 |
2.3.9. Определить силу давления воды на щит и центр давления. Щит прямоугольного сечения шириной b. Глубина воды перед щитом h1, а за щитом h2. Глубина погружения верхней кромки щита a (Рис. 2.3.9.). Давление на свободную поверхность воды слева и справа от щита атмосферное. Расчет выполнить аналитическим способом и проверить графоаналитический.
Вычислить начальное подъемное усилие Т, если коэффициент трения f=0,5, а относительный вес материала щита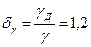 
. Толщина щита e.
Расчет выполнить при данных, приведенных в табл.1.3.9.
Рис. 2.3.9. К задаче 2.3.9.
Таблица 2.3.9.
| № п/п | h1, м | h2, м | а, м | e, м |
| 1 | 1,0 | 0,3 | 0,4 | 0,06 |
| 2 | 2,0 | 0,6 | 0,8 | 0,06 |
| 3 | 3,0 | 0,9 | 1,6 | 0,06 |
| 4 | 3,5 | 1,2 | 1,5 | 0,08 |
| 5 | 4,0 | 1,5 | 2,0 | 0,08 |
| 6 | 4,5 | 2,0 | 2,0 | 0,08 |
2.3.10. Определить силу давления воды на прямоугольный наклонный щит и центр давления. Глубина перед щитом h1, за щитом h2, ширина щита b. Угол наклона щита к горизонту α = 60º (Рис.2.3.10). Расчет выполнить аналитическим и графоаналитическим способами. Найти начальное подъемное усилие исходя из условия, что щит при подъеме вращается вокруг шарнира О, а сила тяги Т действует по перпендикуляру к плоскости затвора. Трением в шарнире пренебречь. Превышение шарнира над горизонтом воды перед щитом а. Относительный вес материала, из которого выполнен щит,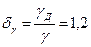 
. Толщина щита е.
Расчет выполнить при данных, приведенных в табл. 2.3.10.
Рис. 2.3.10. К задаче 2.3.10.
Таблица 2.3.10.
| № п/п | h1, м | h2, м | b, м | a, м | e, м |
| 1 | 0,6 | 0 | 0,5 | 0,2 | 0,06 |
| 2 | 1,0 | 0,5 | 0,8 | 0,3 | 0,06 |
| 3 | 1,4 | 0,9 | 1,2 | 0,2 | 0,06 |
| 4 | 1,8 | 0,6 | 1,6 | 0,4 | 0,08 |
| 5 | 2,0 | 1,0 | 2,0 | 0,5 | 0,08 |
| 6 | 2,2 | 0,9 | 2,1 | 0,5 | 0,08 |
2.3.11 Определить аналитическим и графоаналитическим способами силы манометрического давления воды на грани АВ и ВС (Рис.2.3.11.), а также центры давления этих сил. Глубина воды в тоннеле h, высота столба воды над точкой перелома стенки а, угол наклона α=60º, а α2=45º. Расчет выполнить при данных, приведенных в табл. 2.3.11..(b – длина туннеля)
Рис .2.3.11. К задаче 2.3.11
Таблица 2.3.11.
| № п/п | h, м | а,м | b, м |
| 1 | 1,0 | 0,3 | 10 |
| 2 | 1,4 | 0,5 | 8 |
| 3 | 1,8 | 0,6 | 6 |
| 4 | 2,2 | 0,8 | 4 |
| 5 | 2,6 | 1,0 | 2 |
| 6 | 3,0 | 1,2 | 1 |
2.3.12 В резервуар налита ртуть, вода и масло. Высота слоя масла h1, воды h2 и ртути h3. Относительный вес масла δγ=0,8, воды δγ=1 и ртути δγ=13,6.
Построить эпюру манометрического давления и вычислить графоаналитическим способом силу давления на боковую прямоугольную стенку резервуара шириной b. Найти центр давления этой силы относительно линии уреза, определив предварительно графоаналитическим способом центры давления составляющих сил P1, P2 и P3. Угол наклона стенки α (Рис. 2.3.12). Вычислить манометрическое давление на дне и определить силу давления на дно, а также силу, передаваемую на пол, без учета веса резервуара. Площадь дна резервуара bxb.
Расчет выполнить при данных, приведенных в табл. 2.3.12.
|
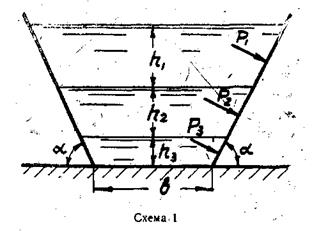
Таблица 2.3.12
| № п/п | h1, м | h2, м | h3, м | b, м | αº |
| 1 | 1,0 | 0,6 | 0,2 | 1,6 | 60 |
| 2 | 0,8 | 0,6 | 0,1 | 1,5 | 45 |
| 3 | 0,6 | 0,5 | 0,05 | 1,0 | 45 |
| 4 | 0,5 | 0,7 | 0,08 | 1,2 | 60 |
| 5 | 0,4 | 0,6 | 0,06 | 1,1 | 45 |
| 6 | 0,9 | 0,8 | 0,15 | 1,4 | 60 |
2.3.13 Определить аналитическим и графоаналитическим способами силы манометрического давления воды на грани плотины АВ, ВС и СD, а также центры давления этих сил (Рис. 2.3.13). Глубина в верхнем бьефе h, угол наклона грани CD к горизонту α1, грани АВ – α2. Ширина бермы – ВС, глубина ее погружения а.
Расчет выполнить на 1 пог.м ширины (вдоль оси плотины) при данных, приведенных в табл.2.3.13.
|
Таблица 2.3.13.
| № п/п | h, м | ВС, м | а, м | α1º | α2º |
| 1 | 2,5 | 0,4 | 1,0 | 45 | 60 |
| 2 | 3,0 | 0,5 | 1,5 | 45 | 60 |
| 3 | 3,5 | 0,6 | 1,5 | 30 | 45 |
| 4 | 4,0 | 0,7 | 2,0 | 30 | 45 |
| 5 | 4,5 | 0,8 | 2,0 | 30 | 30 |
| 6 | 5,0 | 0,9 | 2,5 | 30 | 30 |
2.3.14. Определить силы давления и центры давления на грани полигональной плоской прямоугольной поверхности, показанной на рис. 2.3.14.
Найти равнодействующую и точку приложения равнодействующей.
Расчет выполнить аналитическим и графоаналитическим способами при данных, приведенных в табл. 2.3.14.
|
Таблица 2.3.14.
| № п/п | h1, м | h2, м | h, м | α1º | α2º |
| 1 | 2,0 | 3,8 | 5,0 | 30 | 45 |
| 2 | 2,3 | 4,1 | 5,3 | 30 | 45 |
| 3 | 2,4 | 4,3 | 5,7 | 30 | 45 |
| 4 | 2,8 | 4,8 | 6,0 | 45 | 60 |
| 5 | 3,1 | 5,2 | 6,4 | 45 | 60 |
| 6 | 3,4 | 5,6 | 6,8 | 45 | 60 |
2.3.15 Определить силу натяжения троса, удерживающего наклонный прямоугольный щит, если ширина щита b, глубина воды перед щитом h, угол наклона α (рис.2.3.15).
Найти точку приложения силы давления воды. Расчет выполнить при данных, приведенных в табл. 2.3.15..
|
Таблица 2.3.15
| № п/п | h, м | b, м | αº |
| 1 | 2,0 | 1,8 | 30 |
| 2 | 2,4 | 2,0 | 40 |
| 3 | 2,8 | 2,5 | 50 |
| 4 | 3,2 | 3,0 | 60 |
| 5 | 3,6 | 3,5 | 60 |
| 6 | 4,0 | 4,0 | 70 |
.
3. СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
НА КРИВОЛИНЕЙНЫЕ СИММЕТРИЧНЫЕ ПОВЕРХНОСТИ ПОСТОЯННОЙ КРИВИЗНЫ
Дата: 2019-11-01, просмотров: 1019.
