Пусть задана функция z=f(x,y). Так как x и y - независимы переменные, то одна из них может изменяться, а другая сохранять свое значение.
О: Если существует предел
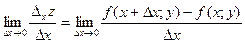 ,
,
то он называется частной производной функции z=f(x,y) в точке М(х,у) по переменной х и обозначается одним их символов:
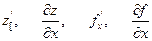 .
.
Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(x,y) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х и у считается постоянной величиной ).
Формула полного дифференциала функции 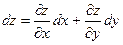
ПРИМЕР: Найти полный дифференциал функции двух переменных

Решение.
Полный дифференциал функции двух переменных находим по формуле:
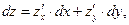
где z/x ; z/y – частные производные данной функции z.
Частные производные берем по обычным формулам дифференцирования для функции одной переменной, причем z/x находим, считая “y” постоянной величиной; аналогично при отыскании z/y считаем “x” постоянным:

Отсюда полный дифференциал функции :
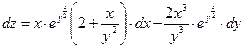
Ряды.
Основные понятия.
Числовым рядом называется выражение вида а1+а2+а3+…+аn+…, где а1, а2, а3,…аn , , называемые членами ряда, образуют бесконечную последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
S1 = a1,
S2 = a1 + a2
S3 = a1 + a2 + an
…………………
S1 = а1+а2+а3+…+аn
при n ®µ имеет конечный предел: 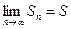 . Этот предел называется суммой сходящегося ряда. Если конечный предел
. Этот предел называется суммой сходящегося ряда. Если конечный предел  не существует , то ряд называется расходящимся.
не существует , то ряд называется расходящимся.
· Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
Ряд может сходиться только при условии, что его общий член an при неограниченном увеличении номера n стремиться к нулю: 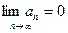 - это необходимый признак сходимости ряда.
- это необходимый признак сходимости ряда.
Если же 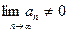 , то ряд расходиться – это достаточный признак расходимости ряда.
, то ряд расходиться – это достаточный признак расходимости ряда.
Для знакоположительных числовых рядовимеют местоследующие достаточные признаки, по которым можно установить их сходимость или расходимость.
1. Признак сравнения. Если члены знакоположительного ряда
а1+а2+а3+…+а n +…, (1)
начиная с некоторого номера, не превосходят соответствующих членов ряда
b 1 + b 2 + b 3 +…+ bn +…, (2)
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия
a + aq + aq2 + aq3 + … + aqn +… ( a > 0),
которая сходиться при ½q½ < 1 и расходиться при ½q½ ≥ 1, и гармонический ряд
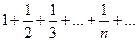 ,
,
Являющийся расходящимся рядом.
2. Признак Даламбера. Если для ряда (1) 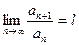 , то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
, то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
· Признак сходимости Лейбница.
Знакочередующимся рядом называется ряд вида
а1 - а2 + а3 - …+ (-1)n-1an + …, (1)
где а1, а2, а3,…аn - положительные числа.
Для знакочередующихся рядов имеет место следующий признак сходимости.
Признак Лейбница. Ряд (1) сходиться, если его слены монотонно убывают по абсолютной величине и общий член стремиться к нулю при n ® µ /
· Абсолютная и условная сходимость знакопеременного ряда.
Ряд а1 +а2+а3+…+аn+… (1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда. Если ряд
½а1 ½+½а2½+½а3½+…+½аn½+…, (2)
составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) также сходиться.
Знакопеременный ряд (1) называется абсолютно сходящимся, если, сходиться ряд (2), составленный из абсолютных величин членов данного ряда (1).
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд , составленный из абсолютных величин его сленов, расходиться..
· Степенные ряды.
Степенным рядом называется ряд вида
а0 + а1х + а2х2 + … + anxn + …, (1)
где а0, а1, а2, а3,…аn ,… - постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда называется совокупность всех значений х, при которых данный ряд сходится.
Нахождение области сходимости состоит из двух этапов.
1. Определяется интервал сходимости степенного ряда, т.е. интервал (-R,R) числовой оси, симметричный относительно точки х = 0 и обладающий тем свойством, что при всех ½х ½ < R – ряд сходиться и притом абсолютно, а при всех ½х ½ > R – ряд расходится. Для этого применяется признак Даламбера к ряду ½а0½ + ½а1½½х ½+ ½а2½½х2½ + … +½ an½½xn½ + …, члены которого есть абсолютные величины членов данного ряда (1).
2. Исследуется сходимость ряда (1) на концах интервала сходимости в точках х = -R и х = R.
Пример 1. Исследовать сходимость ряда
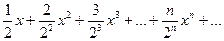
в точках х = 1, х = 3, х = - 2.
Решение.
При х = 1 данный ряд превращается в числовой 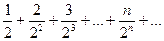
По признаку Даламбера этот ряд сходиться, так как
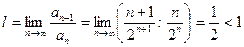
При х = 3 имеем ряд 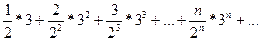
Применяя признак Даламбера, получим
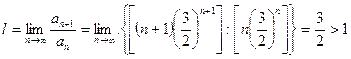 .
.
Следовательно, в точке х = 3 данный ряд расходится.
При х = -2 получаем следующий числовой ряд: -1 + 2 – 3 + 4 - ..+ (-1)n n + …, который расходится (так как не выполняется необходимый признак сходимости ряда).
Пример 2. Исследовать на сходимость степенной ряд 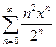 .
.
Решение. Здесь 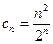 ,
,  ; тогда радиус сходимости
; тогда радиус сходимости
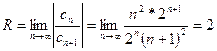 . Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
. Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
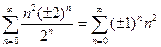 . Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
. Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
Ряды Тейлора и Маклорена
Если функция разложима в некоторой окрестности точки  в степенной ряд по степеням
в степенной ряд по степеням 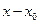 ,то этот ряд имеет вид:
,то этот ряд имеет вид:
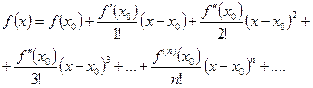 (1.1)
(1.1)
Ряд (1.1) называется рядом Тейлора для функции 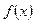 .
.
При 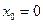 ряд (1.1) принимает вид:
ряд (1.1) принимает вид:

(1.2)
Ряд (1.2) называется рядом Маклорена для функции 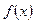 .
.
Таким образом, если функция разлагается в ряд по степеням 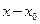 , то этот ряд является рядом Тейлора (или рядом Маклорена при
, то этот ряд является рядом Тейлора (или рядом Маклорена при 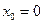 ). Очевидно, если функция разлагается в ряд Тейлора в точке
). Очевидно, если функция разлагается в ряд Тейлора в точке 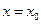 , то она имеет производные любого порядка в точке
, то она имеет производные любого порядка в точке 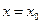 , т.е. бесконечно дифференцируема в точке
, т.е. бесконечно дифференцируема в точке 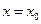
Пример 1.
Записать два первых отличных от нуля члена ряда Тейлора функции
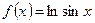 по степеням
по степеням 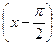 .
.
Решение. Найдём производные функции 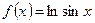 :
:
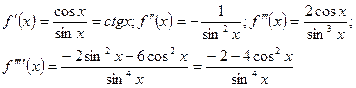
При  получим
получим
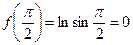 ;
; 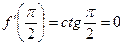 ;
;  ;
;
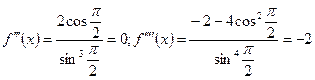 .
.
Запишем формально ряд Тейлора для функции 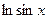 :
:
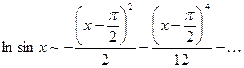 , или, после сокращения
, или, после сокращения 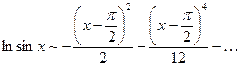 .
.
Разложение функций в ряд Маклорена
Имеют место следующие равенства:
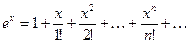 ,
,  , (2.1)
, (2.1)
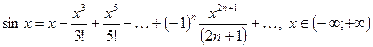 (2.2)
(2.2)
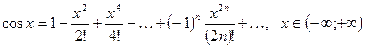 (2.3)
(2.3)
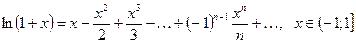 (2.4)
(2.4)
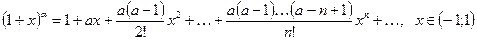 (2.5)
(2.5)
В частном случае, при 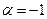 получаем функцию
получаем функцию 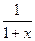 , которая является суммой геометрической прогрессии с первым членом
, которая является суммой геометрической прогрессии с первым членом 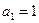 и со знаменателем
и со знаменателем
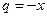 . Поэтому
. Поэтому
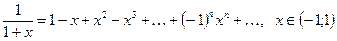 (2.6)
(2.6)
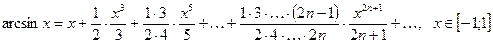 (2.7)
(2.7)
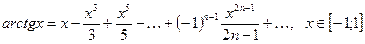 (2.8)
(2.8)
Пример 2.
Разложить функцию 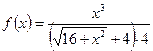 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение. Преобразуем функцию 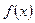 к виду:
к виду:
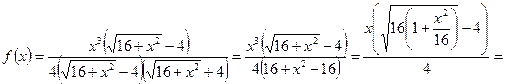
Разложим функцию 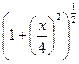 в степенной ряд по формуле (2.5)
в степенной ряд по формуле (2.5)
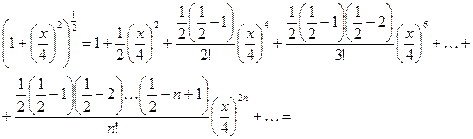
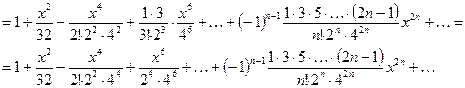
Это разложение верно при 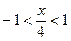 , т.е.
, т.е. 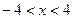 при . Тогда
при . Тогда
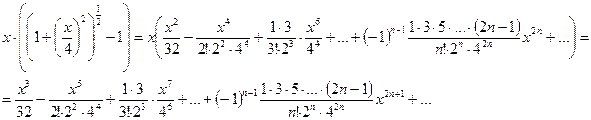
.
Этот ряд сходится при 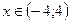 .
.
Пример 3.
Разложить функцию 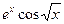 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение: Внутри общего интервала сходимости 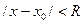
 имеет место формула
имеет место формула
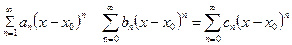 ,
,
где 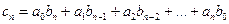 . Тогда, используя разложения (2.1) и (2.3), получим для
. Тогда, используя разложения (2.1) и (2.3), получим для 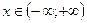
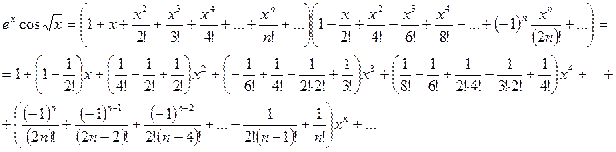
Итак:
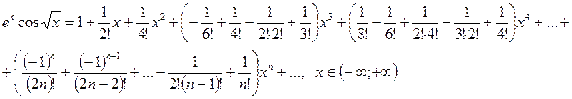
Вычисление определённых интегралов с помощью рядов
ПРИМЕР: Вычислить интеграл 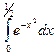 с точностью
с точностью 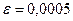 .
.
Решение:
Разложим в ряд Маклорена подынтегральную функцию:
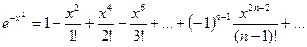 .
.
Это равенство имеет место при всех  . Проинтегрировав его почленно в пределах от 0 до 1, получим:
. Проинтегрировав его почленно в пределах от 0 до 1, получим:
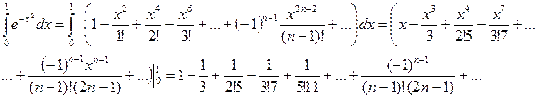 . (3.2)
. (3.2)
Так как вычисления нужно производить с тремя верными десятичными знаками, то погрешность не должна превышать 0,0005.
В правой части равенства стоит знакопеременный ряд. Если сумму знакопеременного ряда заменить суммой его первых n членов, то, как известно, возникающая при этом погрешность не превосходит модуля первого отброшенного члена. Поэтому в разложении (3.2) нужно оставить столько членов, чтобы первый отброшенный был меньше 0, 0005, причём следует учесть погрешности от округления бесконечных десятичных дробей, которые получатся в вычислениях.
Вычисляем члены нашего ряда, начиная со второго:
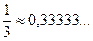 ;
;
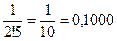 ;
;
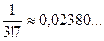 ;
;
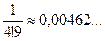 ;
;
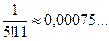 ;
;
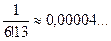 .
.
Следовательно, сохранив в сумме первые шесть членов, получим, что погрешность по абсолютной величине меньше первого отброшенного члена (седьмого члена) и она будет меньше, чем 0,00004, т.е. условие задачи выполнено.
Итак
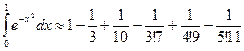 .
.
Теперь нужно вычислить приближённое значение 4 членов этой суммы (т.к. дробь 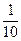 округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей
округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей 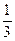 ;
; 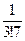 ;
; 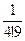 ;
; 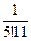 ?
?
Если каждую из них вычислять с тремя десятичными знаками, то погрешность вычислений для каждой дроби будет 0,0005, а для суммы 4-х дробей она будет равна 4 0,0005=0,002, т.е. превзойдёт заданную в условии погрешность.
Если вычисление дробей вести с четырьмя десятичными знаками, то погрешность вычислений для каждой дроби - 0,00005, а для их суммы 4 0,00005=0,0002.
Сложим погрешность вычислений 0,0002 с погрешностью 0,00004 от отбрасывания членов 0,0002+0,00004=0,00024<0,0005.
Итак, промежуточные вычисления выполняем с 4-мя верными знаками:
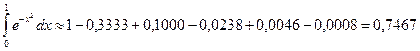
Округляя это число до трёх знаков, получим 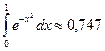 .
.
КОНТРОЛЬНАЯ РАБОТА №1
Вариант
КОНТРОЛЬНАЯ РАБОТА №2
Вариант
ЗАДАНИЕ
Задание 1 – 10. Вычислить предел.
1. 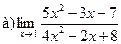 ;
; 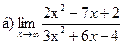 ;
; 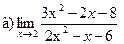 ;
; 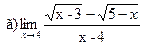
2.  ;
; 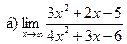 ;
; 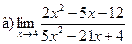 ;
; 
3. 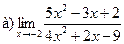 ;
; 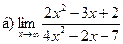 ;
; 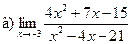 ;
; 
4. 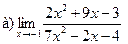 ;
;  ;
;  ;
; 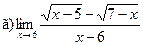
5. 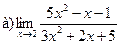 ;
;  ;
; 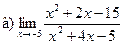 ;
; 
6. 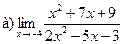 ;
; 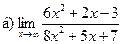 ;
; 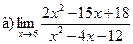 ;
; 
7.  ;
; 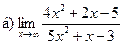 ;
; 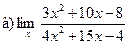 ;
; 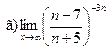
8. 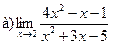 ;
;  ;
; 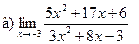 ;
; 
9. 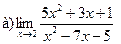 ;
; 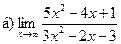 ;
; 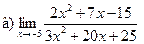 ;
; 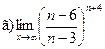
10. 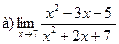 ;
;  ;
;  ;
; 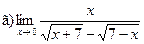
Задание 11-20 Найти производные заданных функций:
11. 
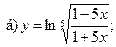
12. 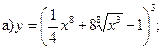
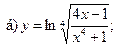
13. 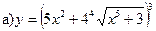 ;
; 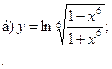
14. 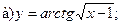
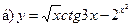
15 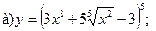
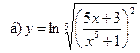
16 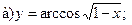
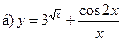
17. 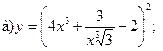
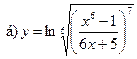
18. 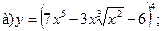
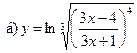
19. 
20. 
Задание 21 – 30 Найти неопределенные интегралы. Результаты проверить дифференцированием.
21. 
22. 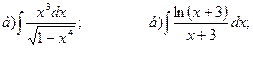
23. 
24. 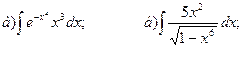
25. 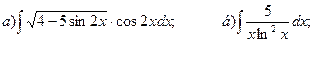
26. 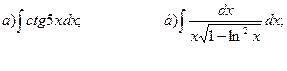
27. 
28. 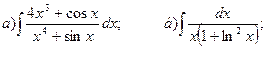
29. 
30. 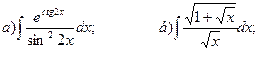
Задание 31 -40 Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж.
31. у = -х2 + 4х - 1; у = -х - 1.
32. у = х2 - 6х + 7; у = х + 1
33. у = -х2 + 6х -5; у = х - 5
34. у = х2 - 6х + 7; у = -х + 7
35. у =-х2 + 6х - 5; у = -х + 1
36. у = х2 + 6х + 7; у = х + 7
37. у = -х2 - 6х - 5; у = х + 1
38. у = х2 + 6х + 7; у = -х + 1
39. у = -х2 - 6х - 6; у = -х - 6
40. у = х2 - 4х + 1; у = х + 1
Задание 41 – 50 Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию у=у0 при х=х0.
41. 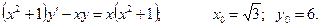

42. 
43. 
44. 
45. 
46. 
47. 
48. 
49. 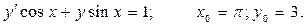
50. 
Задание 51 – 60 Найти частное решение дифференциального уравнения 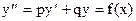 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 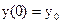 ;
; 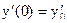 :
:
51. 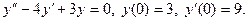
52. 
53. 
54 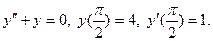
55 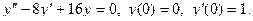
56. 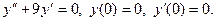
57. 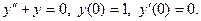
58. 
59. 
60. 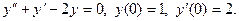
Задание 61 – 70 Найти частные производные и полный дифференциал функции:
61. 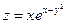
| 66. 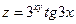
|
62. 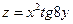
| 67. 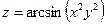
|
63. 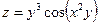
| 68. 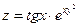
|
64. 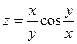
| 69. 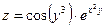
|
65. 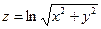
| 70. 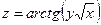
|
Задание 71 – 80 Найти область сходимости ряда степенного:
71. 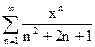 72.
72. 
73. 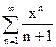 74.
74. 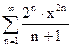
75. 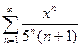 76.
76. 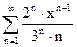
77. 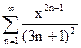 78.
78. 
79. 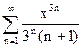 80.
80. 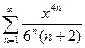
Задание 81 – 90 Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд и почленно интегрируя этот ряд:
81.  82.
82. 
83.  84.
84. 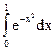
85.  86.
86. 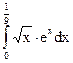
87.  88.
88. 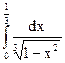
89.  90.
90. 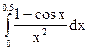
ЛИТЕРАТУРА:
1. Г.Н. Яковлев Алгебра и начала анализа Часть 1, М.: Наука, 1981
2. Г.Н. Яковлев Алгебра и начала анализа Часть 2, М.: Наука, 1981
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, ФМЛ, 1980г.
4. Щипачев В.С. Высшая математика. - М.: Высшая школа, 1985.
5. Богомолов Н.В., Практические занятия по математике. – М.: Высшая
СОДЕРЖАНИЕ
Требования к выполнению и оформлению контрольной работы. 1
Методические указания к выполнению контрольной работы 2
Пределы 2
Производная и ее приложения 6
Интегральное исчисление 9
Дифференциальные уравнения 19
Частные производные первого порядка для функции двух
переменных. Полный дифференциал функции двух переменных. 25
Ряды 26
Ряды Тейлора и Маклорена 28
Контрольная работа 33
ЛИТЕРАТУРА 37
Дата: 2019-11-01, просмотров: 580.