КГБОУ СПО
«Красноярский индустриально-металлургический техникум»
Методические указания
к практическим занятиям по дисциплине
«МАТЕМАТИКА»
для студентов 1 курса
заочной формы обучения
Специальность
22.02.02 «Металлургия цветных металлов»
Красноярск 2014
2014
| СОГЛАСОВАНО на заседании цикловой комиссии «Общеобразовательных дисциплин» Протокол № 9 от 17.05.2011 г. Председатель ЦК А.В. Щагина | Составлены в соответствии с учебным планом и рабочей программой дисциплины «Математика» |
| Составитель: А.В. Щагина | Преподаватель КГБОУ СПО «Красноярский индустриально-металлургический техникум» |
| Рецензенты: Т.И. Граборева | Преподаватель КГБОУ СПО «Красноярский индустриально-металлургический техникум» |
ПРЕДИСЛОВИЕ
Настоящее методическое пособие написано в соответствии с программой базового курса по математике для студентов средних профессиональных учебных заведений, обучающихся по специальности 150402 «Металлургия цветных металлов». Оно содержит как теоретическую часть, так и большое количество примеров и задач.
Основное назначение данного пособия состоит в том, чтобы помочь студенту преодолеть трудности при решении практических работ по математике.
При самостоятельном решении задач многие студенты нуждаются в постоянных консультациях относительно приемов и методов их решения. Такие консультации студент может получить при изучении этого пособия.
Такая форма изложение позволяет студенту сначала познакомиться с приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке навыков при решении практических работ.
Требования к выполнению и оформлению контрольной работы.
1. Каждая работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.
2. На обложке тетради должен быть приклеен титульный лист утвержденного образца: шифр, фамилия имя, отчество студента, адрес, предмет и номер работы.
3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.
4. Решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием.
5. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь.
6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения, например
· Студенты должны соблюдать абзацы, всякую мысль следует начинать с красной строки;
· Важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
· При описании решения задачи краткая запись условия отделяется от решения и в конце ставиться точка;
· Необходимо правильно употреблять математические символы.
7. Решения должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
8. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
9. Если в работе допущены недочеты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.
10. Контрольные работы должны быть выполнены в срок ( в соответствии с учебным планом – графиком).
11. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
12. Студенты, не имеющие зачет по контрольной работе, к экзамену не допускаются.
13. Во время экзамена зачтенные контрольные работы представляются преподавателю вместе с данными методическими указаниями.
14. Контрольная работа имеет 10 вариантов. Вариант выбирается по последней цифре шифра. Если последняя цифра « 0», то студент выполняет 10 вариант.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Пределы.
По данной теме следует сначала изучить Глава IV п.п. 17-18 [1], глава II [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
Основные понятия и определения.
О: Под числовой последовательностью х1, х2, х3, …,х n , …понимается функция х n = f ( n ), заданная на множестве Nнатуральных чисел. Кратко последовательность обозначается в виде {х n } или х n , nÎN.
Число х1 называется первым членом (элементом) последовательности, х2 –вторым,…,х n - общим или n -м членом последовательности.
Способы задания последовательности:
1. формулой общего члена последовательности – позволяет вычислить любой член последовательности по номеру n .
ПРИМЕР:
a ) vn = n 2 +1 => vn ={2,5,10,…, n 2 +1,…}
б) zn =(-1) n * n => zn ={-1,2,-3,4,…,(-1) n * n ,…}
в) yn = 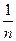 => yn ={1,1/2,1/3,1/4, …,
=> yn ={1,1/2,1/3,1/4, …, 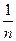 ,…}
,…}
г) un = 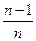 => un = {0,1/2,2/3,3/4,4/5,5/6, …,
=> un = {0,1/2,2/3,3/4,4/5,5/6, …, 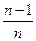 ,…}
,…}
2. рекуррентный –в ней задается начальный элемент х1 (первый член последовательности) и правило определения n –го элемента по( n -1)-му: хn = f ( xn +1 )
ПРИМЕР:
an =2 an -1 - an -2
“-“ - первые члены последовательности не определяется.
Т.к. a 0 и a -1 – не существуют, поэтому а1 и а2 – задают дополнительно.
3.словесно – описание членов последовательности
ПРИМЕР:
А) последовательность ( an ), где an – n -е простое число; начало этой последовательности имеет вид 2; 3; 5; 7; 11; 13; …;
Б) последовательность ( an ), где an =2, если n четное, и an =0, если n нечетное.
Заметим, что в последнем случае легко находиться формула для общего члена: an=1+(-1)n.
О: Последовательность {х n } называется ограниченной, если существует такое число М>0, что для любого nÎN выполняется неравенство
ï х n ï≤ М.
Иначе, последовательность называется неограниченной.
ПРИМЕР: Последовательности yn и un - ограничены, vn и zn - неограниченны.
Монотонность последовательности:
О: Последовательность {х n } называется возрастающей (неубывающей), если для любого n выполняется неравенство an +1 > an ( an +1 ≥ an ).
Аналогично определяется убывающая (не возрастающая) последовательность.
О: Все эти последовательности называются монотонными последовательностями. Последовательности yn , un и vn монотонные, а zn – не монотонная.
О: Если все элементы последовательности {х n } равны одному и тому же числу с , то ее называют постоянной.
Предел числовой последовательности.
Можно заметить, что последовательности un неограниченно приближаются к числу 1.
О: Число а называется пределом последовательности {х n } , если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство │ хn -а│< ε.
Обозначение: 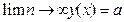
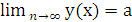
Говорят: последовательность х n имеет предел, равный а при n стремящемся к ∞.
О: Сходящаяся последовательность имеет только один предел. Последовательность не имеющая предела называется расходящейся.
Предел функции.
Пусть функция y = f ( x ) определена в некоторой окрестности точки x 0 , кроме, быть может, самой точки x 0 .
О (на « языке последовательностей», или по Гейне): Число А называется пределом функции y = f ( x ) в точке x 0 , если для любой последовательности допустимых значений аргумента xn, nÎN (xn¹x0), сходящейся к x0 ( т.е. 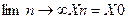
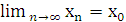 ), последовательность соответствующих значений f ( xn ), n Î N , сходиться к числу А.
), последовательность соответствующих значений f ( xn ), n Î N , сходиться к числу А.
Вторая производная.
Примеры:
· У= 5х3 + 4х –2 - 8х + 4
Y’ = 15x2 – 8x –3 – 8
Y’’= 30x + 24x –4
· У= cos3 x + x7 – e –4x
Y’ = 3cos2x(-sin x) + 7x6 +4e –4x
Y’’ = 6cosx (-sin x) (-sin x) - 3cos2x cos x +42x5 -16e –4x = 6cosx sin 2x - 3cos3 x +42x5 -16e –4x
Интегральное исчисление
Определение 1. Функция F ( x ) называется первообразной для функции f ( x ) в промежутке 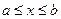 , если в любой точке этого промежутка ее производная равна f ( x ):
, если в любой точке этого промежутка ее производная равна f ( x ):
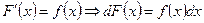 ,
, 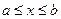 . (1)
. (1)
Определение 2. Совокупность всех первообразных функций F(x) + с для функции f ( x ) на некотором промежутке называется неопределённым интегралом и обозначается

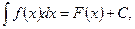 (2)
(2)
где f ( x ) dx называется подынтегральным выражением, х - переменной интегрирования, а С -произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например 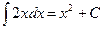 , т.к.
, т.к. 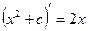
1. Метод непосредственного интегрирования.
Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводятся к одному или нескольким табличным интегралам.
1. 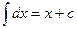
| 9. 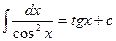
|
2. 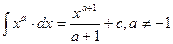
| 10. 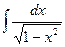 = = 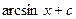
|
3. 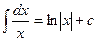
| 11. 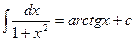
|
4. 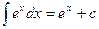
| 12. 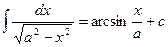
|
5. 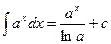
| 13. 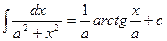
|
6. 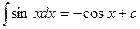
| 14. 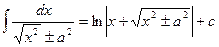
|
7. 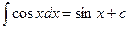
| 15. 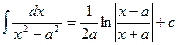
|
8. 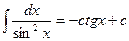
|
Примечание. Формулы верны, когда х является независимой переменной, а также когда х является функцией другой переменной: х=х(t).
Свойства неопределённого интеграла
1) 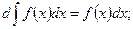 2)
2) 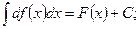 3)
3) 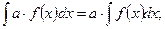
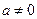
4) 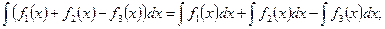
Примеры
1) 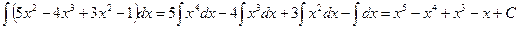
2) 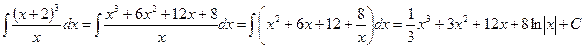
Примеры:
l) 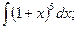 2)
2) 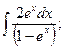
Решение:
1) положим 1 + х = z. Продифференцируем это неравенство: 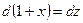 или dx = dz .
или dx = dz .
Заменим в интеграле: 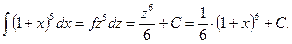
2) Сделав замену: 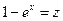 , получим
, получим 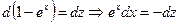 . Тогда
. Тогда
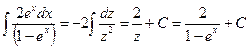
Дифференциальные уравнения
Обыкновенным дифференциальным уравнением называется равенство, содержащее независимую переменную x, неизвестную функцию y и её производные :
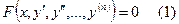

Порядок старшей производной уравнения (1) называется порядком уравнения. Решением уравнения (1) называется функция 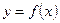 , обращающая уравнение в тождество. Процесс нахождения решения называется интегрированием дифференциального уравнения. График решения на плоскости (x,y) называется интегральной кривой.
, обращающая уравнение в тождество. Процесс нахождения решения называется интегрированием дифференциального уравнения. График решения на плоскости (x,y) называется интегральной кривой.
Например, функция 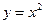 удовлетворяет уравнению
удовлетворяет уравнению 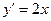 и поэтому является его решением , однако это решение не единственно, т.к. семейство функций
и поэтому является его решением , однако это решение не единственно, т.к. семейство функций 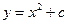 , где
, где 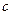 – произвольная константа, также решение уравнения. Говорят, что функция (семейство функций)
– произвольная константа, также решение уравнения. Говорят, что функция (семейство функций) 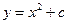 является общим решением. Общее решение может быть найдено в явном, параметрическом или неявном виде, в любом случае оно должно зависеть от n констант
является общим решением. Общее решение может быть найдено в явном, параметрическом или неявном виде, в любом случае оно должно зависеть от n констант 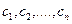 . Если общее решение получено в неявном виде, то его часто называют общим интегралом уравнения.
. Если общее решение получено в неявном виде, то его часто называют общим интегралом уравнения.
Всякое решение, получающееся из общего при некоторых конкретных значениях констант, называется частным решением. Так, в рассмотренном примере 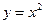 решение является частным, оно получается из общего при
решение является частным, оно получается из общего при 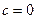 Задачу нахождения частного решения в общей постановке можно сформулировать следующим образом:
Задачу нахождения частного решения в общей постановке можно сформулировать следующим образом:
найти частное решение уравнения (1) , удовлетворяющее условиям
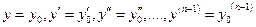 (2)
(2)
Геометрически это означает, что интегральная кривая частного решения должна проходить через точку (x0,y0) и иметь заданные производные в этой точке, равные указанным значениям. Условия (2) называются начальными данными.
В общем случае не всякое решение получается из общего при конкретных (числовых) значениях констант. Решение, которое не содержится в общем решении ни при каких числовых значениях констант, называется особым решением.
При решении дифференциальных уравнений следует иметь в виду, что существуют типы уравнений, для которых известны шаблонные методы решения. Поэтому процесс решения разбивается, как правило, на три этапа:
1. Распознание типа решаемого уравнения либо приведение его к известному типу.
2. Применение известного шаблонного метода решения к распознанному уравнению.
3. Интегрирование уравнения (взятие интегралов).
Первый этап - идеологический, требует навыка, опыта, набитие руки. Второй этап - справочный, требует хорошей памяти, умения запоминать. Третий этап - технический, требует владения техникой интегрирования (взятие неопределенных интегралов).
Учитывая, что 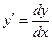 , иногда дифференциальное уравнение записывают в дифференциалах. Например, уравнение
, иногда дифференциальное уравнение записывают в дифференциалах. Например, уравнение 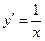 можно записать в виде
можно записать в виде 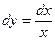 .
.
Рассмотрим некоторые типы уравнений и методы их решения.
1. Простейшее дифференциальное уравнение 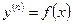
Интегрируя n раз обе части уравнения, найдем общее решение, зависящее от n констант 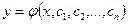
Пример 1 Найти частное решение уравнения 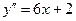 с начальными данными: при x=0 y=1,
с начальными данными: при x=0 y=1, 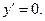 Интегрируем дважды
Интегрируем дважды 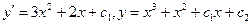
Из начальных условий следует: 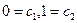 . Таким образом,
. Таким образом, 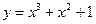 .
.
2. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение y '= f ( x , y ) называется уравнением с разделяющимися переменными, если имеет следующий вид: 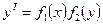 (3)
(3)
В предположении, что f 2 ( y ) 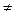 0, уравнение с разделяющимися переменными (3) можно переписать в виде (разделить переменные):
0, уравнение с разделяющимися переменными (3) можно переписать в виде (разделить переменные):
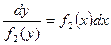 (4)
(4)
Уравнение вида (4) называется уравнением с разделёнными переменными.
При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться следующим алгоритмом:
1) разделить переменные (с учётом условий, когда это можно делать);
2) проинтегрировать почленно полученное уравнение с разделёнными переменными;
3) найти его общий интеграл;
4) выяснить, имеет ли уравнение (5) решения, не получающиеся из общего интеграла;
5) найти частный интеграл (или решение), удовлетворяющий начальным условиям (в случае задачи Коши).
Пример. Найти частное решение уравнения:  2у' = 1 - Зх2; у
2у' = 1 - Зх2; у 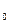 = 3 при х
= 3 при х 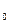 = 0
= 0
Решение: это уравнение с разделяющимися переменными. Представим его в дифференциалах.
Учитывая, что 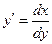 получим 2у— = 1-3х
получим 2у— = 1-3х 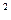 .
.
Разделим переменные:
2 ydy = (1 - Зх2 ) dx . Интегрируя обе части последнего равенства, найдём
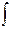 2 ydy =
2 ydy = 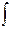 (1 - Зх2 ) dx , т.е. у2=х-х3+С. Подставив начальные значения х0 =1, уо=3,найдём С: 9=1-1+С, т.е. С=9. Следовательно, искомый частный интеграл будет у2=х-х3+9, или х3+у2-х-9 = 0
(1 - Зх2 ) dx , т.е. у2=х-х3+С. Подставив начальные значения х0 =1, уо=3,найдём С: 9=1-1+С, т.е. С=9. Следовательно, искомый частный интеграл будет у2=х-х3+9, или х3+у2-х-9 = 0
Решение:
I ) Разрешим уравнение относительно производной 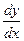 :
: 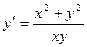 .
.
Поделив числитель и знаменатель правой части уравнения на х2, получим
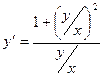 (*)
(*)
Замены: u=y/x и 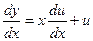 в уравнение (*).
в уравнение (*).
Уравнение (*) преобразуется в уравнение с разделяющимися переменными:
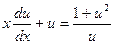 Û
Û 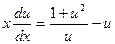 Û
Û 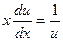
откуда 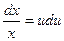
Интегрируя это уравнение, получим 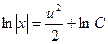 Û
Û 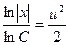 т.е. х=С
т.е. х=С 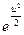
Заменяя в последнем равенстве u на y/x, окончательно получаем общее решение данного уравнения х=С 
II ) Используя начальные условия у(2)=0, подставляем в общее решение данного уравнения х=С  , заданные значения переменных х=2, у=0 – тем самым определяем значение произвольной постоянной С: 2=С
, заданные значения переменных х=2, у=0 – тем самым определяем значение произвольной постоянной С: 2=С 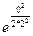 Û С= 2.
Û С= 2.
Итак, искомое частное решение х=2 
Решение.
Полный дифференциал функции двух переменных находим по формуле:
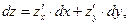
где z/x ; z/y – частные производные данной функции z.
Частные производные берем по обычным формулам дифференцирования для функции одной переменной, причем z/x находим, считая “y” постоянной величиной; аналогично при отыскании z/y считаем “x” постоянным:
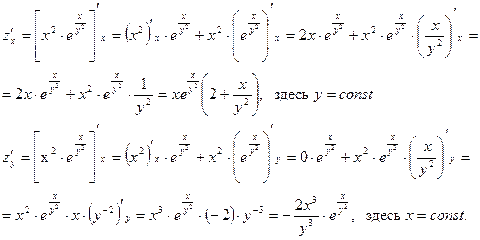
Отсюда полный дифференциал функции :
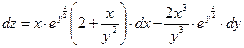
Ряды.
Основные понятия.
Числовым рядом называется выражение вида а1+а2+а3+…+аn+…, где а1, а2, а3,…аn , , называемые членами ряда, образуют бесконечную последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
S1 = a1,
S2 = a1 + a2
S3 = a1 + a2 + an
…………………
S1 = а1+а2+а3+…+аn
при n ®µ имеет конечный предел: 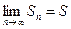 . Этот предел называется суммой сходящегося ряда. Если конечный предел
. Этот предел называется суммой сходящегося ряда. Если конечный предел 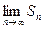 не существует , то ряд называется расходящимся.
не существует , то ряд называется расходящимся.
· Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
Ряд может сходиться только при условии, что его общий член an при неограниченном увеличении номера n стремиться к нулю: 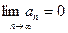 - это необходимый признак сходимости ряда.
- это необходимый признак сходимости ряда.
Если же 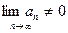 , то ряд расходиться – это достаточный признак расходимости ряда.
, то ряд расходиться – это достаточный признак расходимости ряда.
Для знакоположительных числовых рядовимеют местоследующие достаточные признаки, по которым можно установить их сходимость или расходимость.
1. Признак сравнения. Если члены знакоположительного ряда
а1+а2+а3+…+а n +…, (1)
начиная с некоторого номера, не превосходят соответствующих членов ряда
b 1 + b 2 + b 3 +…+ bn +…, (2)
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия
a + aq + aq2 + aq3 + … + aqn +… ( a > 0),
которая сходиться при ½q½ < 1 и расходиться при ½q½ ≥ 1, и гармонический ряд
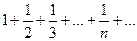 ,
,
Являющийся расходящимся рядом.
2. Признак Даламбера. Если для ряда (1) 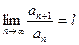 , то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
, то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
· Признак сходимости Лейбница.
Знакочередующимся рядом называется ряд вида
а1 - а2 + а3 - …+ (-1)n-1an + …, (1)
где а1, а2, а3,…аn - положительные числа.
Для знакочередующихся рядов имеет место следующий признак сходимости.
Признак Лейбница. Ряд (1) сходиться, если его слены монотонно убывают по абсолютной величине и общий член стремиться к нулю при n ® µ /
· Абсолютная и условная сходимость знакопеременного ряда.
Ряд а1 +а2+а3+…+аn+… (1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда. Если ряд
½а1 ½+½а2½+½а3½+…+½аn½+…, (2)
составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) также сходиться.
Знакопеременный ряд (1) называется абсолютно сходящимся, если, сходиться ряд (2), составленный из абсолютных величин членов данного ряда (1).
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд , составленный из абсолютных величин его сленов, расходиться..
· Степенные ряды.
Степенным рядом называется ряд вида
а0 + а1х + а2х2 + … + anxn + …, (1)
где а0, а1, а2, а3,…аn ,… - постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда называется совокупность всех значений х, при которых данный ряд сходится.
Нахождение области сходимости состоит из двух этапов.
1. Определяется интервал сходимости степенного ряда, т.е. интервал (-R,R) числовой оси, симметричный относительно точки х = 0 и обладающий тем свойством, что при всех ½х ½ < R – ряд сходиться и притом абсолютно, а при всех ½х ½ > R – ряд расходится. Для этого применяется признак Даламбера к ряду ½а0½ + ½а1½½х ½+ ½а2½½х2½ + … +½ an½½xn½ + …, члены которого есть абсолютные величины членов данного ряда (1).
2. Исследуется сходимость ряда (1) на концах интервала сходимости в точках х = -R и х = R.
Пример 1. Исследовать сходимость ряда
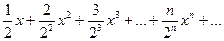
в точках х = 1, х = 3, х = - 2.
Решение.
При х = 1 данный ряд превращается в числовой 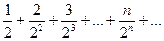
По признаку Даламбера этот ряд сходиться, так как
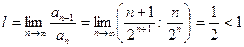
При х = 3 имеем ряд 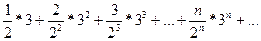
Применяя признак Даламбера, получим
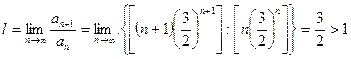 .
.
Следовательно, в точке х = 3 данный ряд расходится.
При х = -2 получаем следующий числовой ряд: -1 + 2 – 3 + 4 - ..+ (-1)n n + …, который расходится (так как не выполняется необходимый признак сходимости ряда).
Пример 2. Исследовать на сходимость степенной ряд 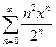 .
.
Решение. Здесь 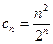 ,
,  ; тогда радиус сходимости
; тогда радиус сходимости
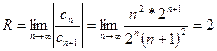 . Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
. Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
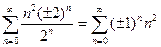 . Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
. Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
Ряды Тейлора и Маклорена
Если функция разложима в некоторой окрестности точки 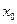 в степенной ряд по степеням
в степенной ряд по степеням 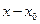 ,то этот ряд имеет вид:
,то этот ряд имеет вид:
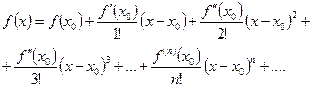 (1.1)
(1.1)
Ряд (1.1) называется рядом Тейлора для функции 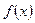 .
.
При 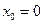 ряд (1.1) принимает вид:
ряд (1.1) принимает вид:
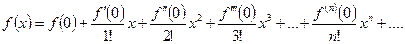
(1.2)
Ряд (1.2) называется рядом Маклорена для функции 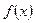 .
.
Таким образом, если функция разлагается в ряд по степеням 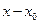 , то этот ряд является рядом Тейлора (или рядом Маклорена при
, то этот ряд является рядом Тейлора (или рядом Маклорена при 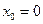 ). Очевидно, если функция разлагается в ряд Тейлора в точке
). Очевидно, если функция разлагается в ряд Тейлора в точке 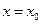 , то она имеет производные любого порядка в точке
, то она имеет производные любого порядка в точке 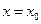 , т.е. бесконечно дифференцируема в точке
, т.е. бесконечно дифференцируема в точке 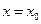
Пример 1.
Записать два первых отличных от нуля члена ряда Тейлора функции
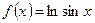 по степеням
по степеням 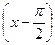 .
.
Решение. Найдём производные функции 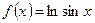 :
:
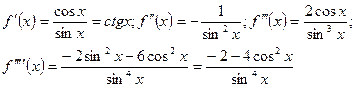
При  получим
получим
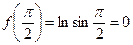 ;
; 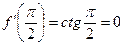 ;
; 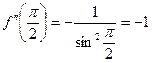 ;
;
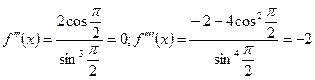 .
.
Запишем формально ряд Тейлора для функции 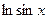 :
:
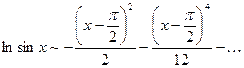 , или, после сокращения
, или, после сокращения 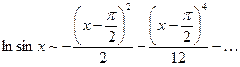 .
.
Разложение функций в ряд Маклорена
Имеют место следующие равенства:
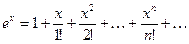 ,
, 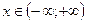 , (2.1)
, (2.1)
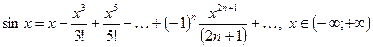 (2.2)
(2.2)
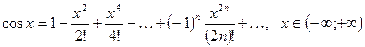 (2.3)
(2.3)
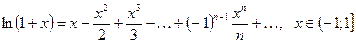 (2.4)
(2.4)
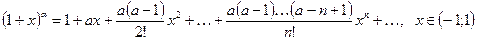 (2.5)
(2.5)
В частном случае, при 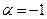 получаем функцию
получаем функцию 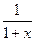 , которая является суммой геометрической прогрессии с первым членом
, которая является суммой геометрической прогрессии с первым членом 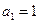 и со знаменателем
и со знаменателем
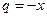 . Поэтому
. Поэтому
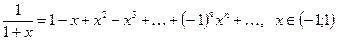 (2.6)
(2.6)
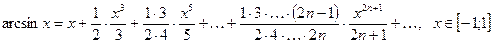 (2.7)
(2.7)
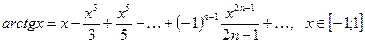 (2.8)
(2.8)
Пример 2.
Разложить функцию 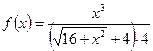 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение. Преобразуем функцию 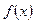 к виду:
к виду:
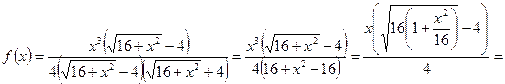
Разложим функцию 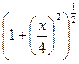 в степенной ряд по формуле (2.5)
в степенной ряд по формуле (2.5)
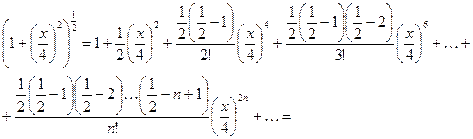
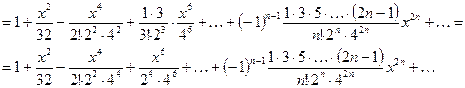
Это разложение верно при 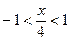 , т.е.
, т.е. 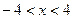 при . Тогда
при . Тогда
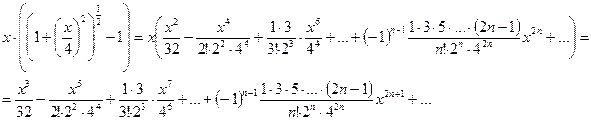
.
Этот ряд сходится при 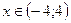 .
.
Пример 3.
Разложить функцию 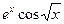 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение: Внутри общего интервала сходимости 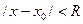
 имеет место формула
имеет место формула
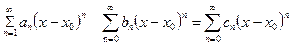 ,
,
где 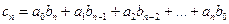 . Тогда, используя разложения (2.1) и (2.3), получим для
. Тогда, используя разложения (2.1) и (2.3), получим для 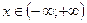
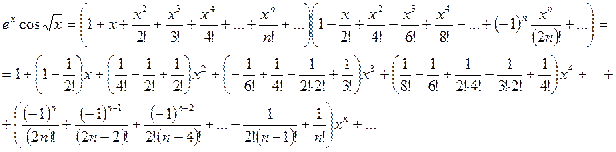
Итак:
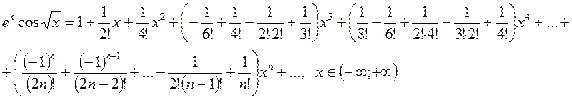
Вычисление определённых интегралов с помощью рядов
ПРИМЕР: Вычислить интеграл 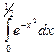 с точностью
с точностью 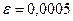 .
.
Решение:
Разложим в ряд Маклорена подынтегральную функцию:
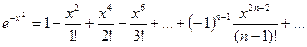 .
.
Это равенство имеет место при всех 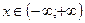 . Проинтегрировав его почленно в пределах от 0 до 1, получим:
. Проинтегрировав его почленно в пределах от 0 до 1, получим:
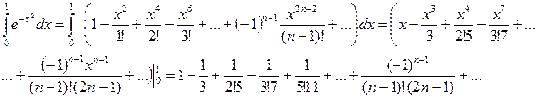 . (3.2)
. (3.2)
Так как вычисления нужно производить с тремя верными десятичными знаками, то погрешность не должна превышать 0,0005.
В правой части равенства стоит знакопеременный ряд. Если сумму знакопеременного ряда заменить суммой его первых n членов, то, как известно, возникающая при этом погрешность не превосходит модуля первого отброшенного члена. Поэтому в разложении (3.2) нужно оставить столько членов, чтобы первый отброшенный был меньше 0, 0005, причём следует учесть погрешности от округления бесконечных десятичных дробей, которые получатся в вычислениях.
Вычисляем члены нашего ряда, начиная со второго:
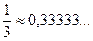 ;
;
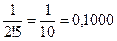 ;
;
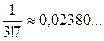 ;
;
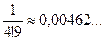 ;
;
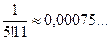 ;
;
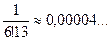 .
.
Следовательно, сохранив в сумме первые шесть членов, получим, что погрешность по абсолютной величине меньше первого отброшенного члена (седьмого члена) и она будет меньше, чем 0,00004, т.е. условие задачи выполнено.
Итак
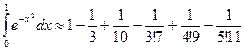 .
.
Теперь нужно вычислить приближённое значение 4 членов этой суммы (т.к. дробь 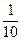 округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей
округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей 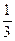 ;
; 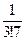 ;
; 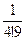 ;
; 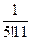 ?
?
Если каждую из них вычислять с тремя десятичными знаками, то погрешность вычислений для каждой дроби будет 0,0005, а для суммы 4-х дробей она будет равна 4 0,0005=0,002, т.е. превзойдёт заданную в условии погрешность.
Если вычисление дробей вести с четырьмя десятичными знаками, то погрешность вычислений для каждой дроби - 0,00005, а для их суммы 4 0,00005=0,0002.
Сложим погрешность вычислений 0,0002 с погрешностью 0,00004 от отбрасывания членов 0,0002+0,00004=0,00024<0,0005.
Итак, промежуточные вычисления выполняем с 4-мя верными знаками:
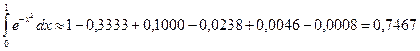
Округляя это число до трёх знаков, получим 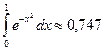 .
.
КОНТРОЛЬНАЯ РАБОТА №1
Вариант
КОНТРОЛЬНАЯ РАБОТА №2
Вариант
ЗАДАНИЕ
Задание 1 – 10. Вычислить предел.
1. 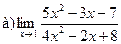 ;
; 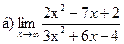 ;
; 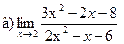 ;
; 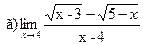
2. 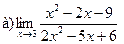 ;
; 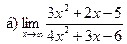 ;
; 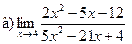 ;
; 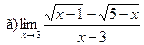
3. 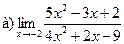 ;
; 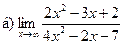 ;
; 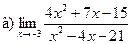 ;
; 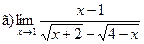
4. 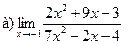 ;
; 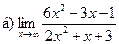 ;
; 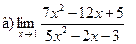 ;
; 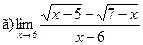
5. 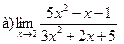 ;
; 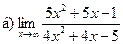 ;
; 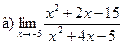 ;
; 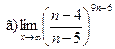
6. 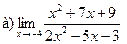 ;
; 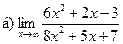 ;
; 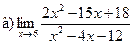 ;
; 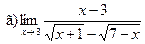
7. 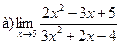 ;
; 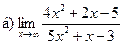 ;
; 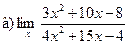 ;
; 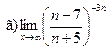
8. 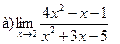 ;
; 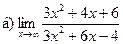 ;
; 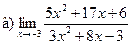 ;
; 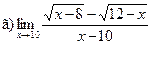
9. 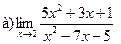 ;
; 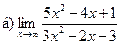 ;
; 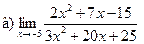 ;
; 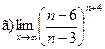
10. 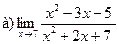 ;
; 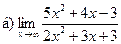 ;
; 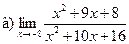 ;
; 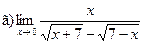
Задание 11-20 Найти производные заданных функций:
11. 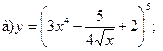
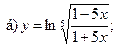
12. 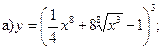
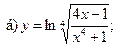
13. 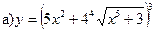 ;
; 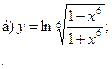
14. 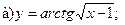
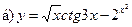
15 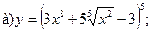
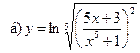
16 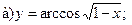
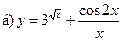
17. 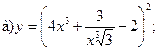
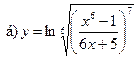
18. 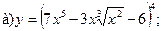
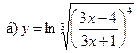
19. 
20. 
Задание 21 – 30 Найти неопределенные интегралы. Результаты проверить дифференцированием.
21. 
22. 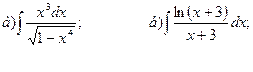
23. 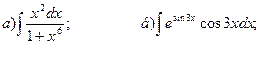
24. 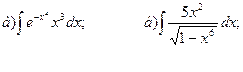
25. 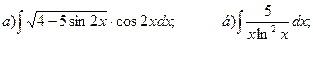
26. 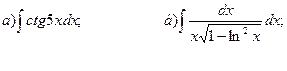
27. 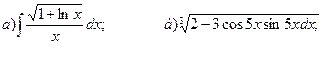
28. 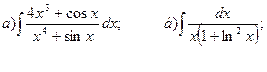
29. 
30. 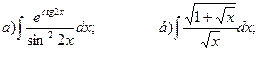
Задание 31 -40 Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж.
31. у = -х2 + 4х - 1; у = -х - 1.
32. у = х2 - 6х + 7; у = х + 1
33. у = -х2 + 6х -5; у = х - 5
34. у = х2 - 6х + 7; у = -х + 7
35. у =-х2 + 6х - 5; у = -х + 1
36. у = х2 + 6х + 7; у = х + 7
37. у = -х2 - 6х - 5; у = х + 1
38. у = х2 + 6х + 7; у = -х + 1
39. у = -х2 - 6х - 6; у = -х - 6
40. у = х2 - 4х + 1; у = х + 1
Задание 41 – 50 Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию у=у0 при х=х0.
41. 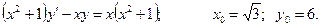

42. 
43. 
44. 
45. 
46. 
47. 
48. 
49. 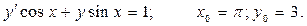
50. 
Задание 51 – 60 Найти частное решение дифференциального уравнения 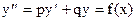 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 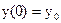 ;
; 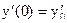 :
:
51. 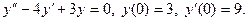
52. 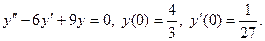
53. 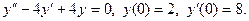
54 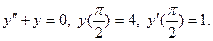
55 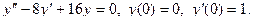
56. 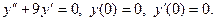
57. 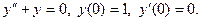
58. 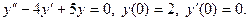
59. 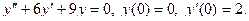
60. 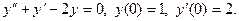
Задание 61 – 70 Найти частные производные и полный дифференциал функции:
61. 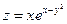
| 66. 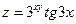
|
62. 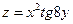
| 67. 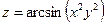
|
63. 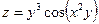
| 68. 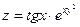
|
64. 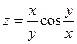
| 69. 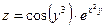
|
65. 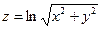
| 70. 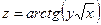
|
Задание 71 – 80 Найти область сходимости ряда степенного:
71. 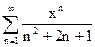 72.
72. 
73. 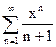 74.
74. 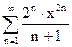
75. 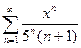 76.
76. 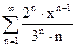
77. 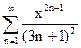 78.
78. 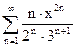
79. 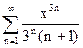 80.
80. 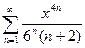
Задание 81 – 90 Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд и почленно интегрируя этот ряд:
81. 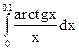 82.
82. 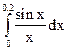
83.  84.
84. 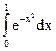
85. 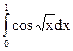 86.
86. 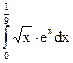
87. 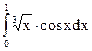 88.
88. 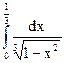
89. 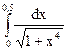 90.
90. 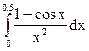
ЛИТЕРАТУРА:
1. Г.Н. Яковлев Алгебра и начала анализа Часть 1, М.: Наука, 1981
2. Г.Н. Яковлев Алгебра и начала анализа Часть 2, М.: Наука, 1981
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, ФМЛ, 1980г.
4. Щипачев В.С. Высшая математика. - М.: Высшая школа, 1985.
5. Богомолов Н.В., Практические занятия по математике. – М.: Высшая
СОДЕРЖАНИЕ
Требования к выполнению и оформлению контрольной работы. 1
Методические указания к выполнению контрольной работы 2
Пределы 2
Производная и ее приложения 6
Интегральное исчисление 9
Дифференциальные уравнения 19
Частные производные первого порядка для функции двух
переменных. Полный дифференциал функции двух переменных. 25
Ряды 26
Ряды Тейлора и Маклорена 28
Контрольная работа 33
ЛИТЕРАТУРА 37
КГБОУ СПО
«Красноярский индустриально-металлургический техникум»
Методические указания
к практическим занятиям по дисциплине
«МАТЕМАТИКА»
для студентов 1 курса
заочной формы обучения
Специальность
22.02.02 «Металлургия цветных металлов»
Красноярск 2014
2014
| СОГЛАСОВАНО на заседании цикловой комиссии «Общеобразовательных дисциплин» Протокол № 9 от 17.05.2011 г. Председатель ЦК А.В. Щагина | Составлены в соответствии с учебным планом и рабочей программой дисциплины «Математика» |
| Составитель: А.В. Щагина | Преподаватель КГБОУ СПО «Красноярский индустриально-металлургический техникум» |
| Рецензенты: Т.И. Граборева | Преподаватель КГБОУ СПО «Красноярский индустриально-металлургический техникум» |
ПРЕДИСЛОВИЕ
Настоящее методическое пособие написано в соответствии с программой базового курса по математике для студентов средних профессиональных учебных заведений, обучающихся по специальности 150402 «Металлургия цветных металлов». Оно содержит как теоретическую часть, так и большое количество примеров и задач.
Основное назначение данного пособия состоит в том, чтобы помочь студенту преодолеть трудности при решении практических работ по математике.
При самостоятельном решении задач многие студенты нуждаются в постоянных консультациях относительно приемов и методов их решения. Такие консультации студент может получить при изучении этого пособия.
Такая форма изложение позволяет студенту сначала познакомиться с приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке навыков при решении практических работ.
Требования к выполнению и оформлению контрольной работы.
1. Каждая работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.
2. На обложке тетради должен быть приклеен титульный лист утвержденного образца: шифр, фамилия имя, отчество студента, адрес, предмет и номер работы.
3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.
4. Решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием.
5. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь.
6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения, например
· Студенты должны соблюдать абзацы, всякую мысль следует начинать с красной строки;
· Важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
· При описании решения задачи краткая запись условия отделяется от решения и в конце ставиться точка;
· Необходимо правильно употреблять математические символы.
7. Решения должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
8. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
9. Если в работе допущены недочеты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.
10. Контрольные работы должны быть выполнены в срок ( в соответствии с учебным планом – графиком).
11. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
12. Студенты, не имеющие зачет по контрольной работе, к экзамену не допускаются.
13. Во время экзамена зачтенные контрольные работы представляются преподавателю вместе с данными методическими указаниями.
14. Контрольная работа имеет 10 вариантов. Вариант выбирается по последней цифре шифра. Если последняя цифра « 0», то студент выполняет 10 вариант.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Пределы.
По данной теме следует сначала изучить Глава IV п.п. 17-18 [1], глава II [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
Основные понятия и определения.
О: Под числовой последовательностью х1, х2, х3, …,х n , …понимается функция х n = f ( n ), заданная на множестве Nнатуральных чисел. Кратко последовательность обозначается в виде {х n } или х n , nÎN.
Число х1 называется первым членом (элементом) последовательности, х2 –вторым,…,х n - общим или n -м членом последовательности.
Способы задания последовательности:
1. формулой общего члена последовательности – позволяет вычислить любой член последовательности по номеру n .
ПРИМЕР:
a ) vn = n 2 +1 => vn ={2,5,10,…, n 2 +1,…}
б) zn =(-1) n * n => zn ={-1,2,-3,4,…,(-1) n * n ,…}
в) yn = 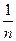 => yn ={1,1/2,1/3,1/4, …,
=> yn ={1,1/2,1/3,1/4, …, 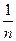 ,…}
,…}
г) un = 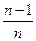 => un = {0,1/2,2/3,3/4,4/5,5/6, …,
=> un = {0,1/2,2/3,3/4,4/5,5/6, …, 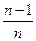 ,…}
,…}
2. рекуррентный –в ней задается начальный элемент х1 (первый член последовательности) и правило определения n –го элемента по( n -1)-му: хn = f ( xn +1 )
ПРИМЕР:
an =2 an -1 - an -2
“-“ - первые члены последовательности не определяется.
Т.к. a 0 и a -1 – не существуют, поэтому а1 и а2 – задают дополнительно.
3.словесно – описание членов последовательности
ПРИМЕР:
А) последовательность ( an ), где an – n -е простое число; начало этой последовательности имеет вид 2; 3; 5; 7; 11; 13; …;
Б) последовательность ( an ), где an =2, если n четное, и an =0, если n нечетное.
Заметим, что в последнем случае легко находиться формула для общего члена: an=1+(-1)n.
О: Последовательность {х n } называется ограниченной, если существует такое число М>0, что для любого nÎN выполняется неравенство
ï х n ï≤ М.
Иначе, последовательность называется неограниченной.
ПРИМЕР: Последовательности yn и un - ограничены, vn и zn - неограниченны.
Монотонность последовательности:
О: Последовательность {х n } называется возрастающей (неубывающей), если для любого n выполняется неравенство an +1 > an ( an +1 ≥ an ).
Аналогично определяется убывающая (не возрастающая) последовательность.
О: Все эти последовательности называются монотонными последовательностями. Последовательности yn , un и vn монотонные, а zn – не монотонная.
О: Если все элементы последовательности {х n } равны одному и тому же числу с , то ее называют постоянной.
Предел числовой последовательности.
Можно заметить, что последовательности un неограниченно приближаются к числу 1.
О: Число а называется пределом последовательности {х n } , если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство │ хn -а│< ε.
Обозначение: 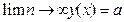
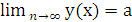
Говорят: последовательность х n имеет предел, равный а при n стремящемся к ∞.
О: Сходящаяся последовательность имеет только один предел. Последовательность не имеющая предела называется расходящейся.
Предел функции.
Пусть функция y = f ( x ) определена в некоторой окрестности точки x 0 , кроме, быть может, самой точки x 0 .
О (на « языке последовательностей», или по Гейне): Число А называется пределом функции y = f ( x ) в точке x 0 , если для любой последовательности допустимых значений аргумента xn, nÎN (xn¹x0), сходящейся к x0 ( т.е. 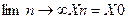
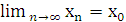 ), последовательность соответствующих значений f ( xn ), n Î N , сходиться к числу А.
), последовательность соответствующих значений f ( xn ), n Î N , сходиться к числу А.
Техника вычисления пределов.
При вычисление предела элементарной функции f(x) приходиться сталкиваться с двумя различными типами примеров.
1. Функция f(x) определена в предельной точке х = а. Тогда 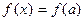
2. Функция f(x) в предельной точке х = а не определена или же вычисляется предел функции при х ® ¥ . Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях ( наиболее простых) вопрос сводиться непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними.
Более сложными случаями нахождения предела являются такие, когда
функция f(x) в точке х = а или при х ® ¥ представляет собой неопределенность
( типа 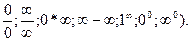
Приведем основные теоремы, на которых основано вычисление пределов.
1) Если существуют 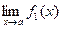 и
и 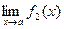 , то
, то
· 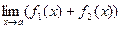 =
= 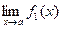 +
+ 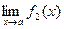
· 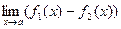 =
= 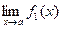 -
- 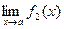
· 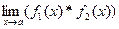 =
= 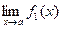 *
* 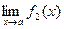
· 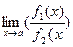 =
= 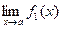 /
/ 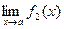 при
при 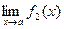 ¹ 0
¹ 0
2) 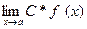 = С*
= С* 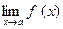 , где С – некоторое число
, где С – некоторое число
3) Связь между бесконечно малой и бесконечно большой величинами (С– некоторое число): 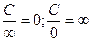
Рассмотрим некоторые ПРИМЕРЫ:
Задание 1. Найти предел функции 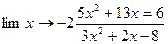
Решение: Имеем неопределенность вида 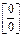 . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель 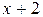 , который при
, который при 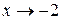 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
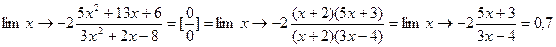
Задание 2. Найти предел функции 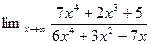
Решение : Имеем неопределенность вида  . Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
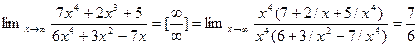
Задание 3. Найти предел функции 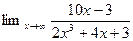
Решение: Имеем неопределенность вида 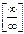 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
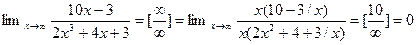
Задание 4. Найти предел функции 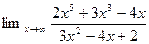
Решение: Имеем неопределенность вида 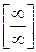 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
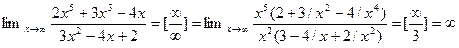
Задание 5. Найти предел функции 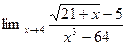
Решение: Имеем неопределенность вида 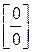 . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель 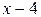 , который при
, который при 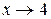 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.

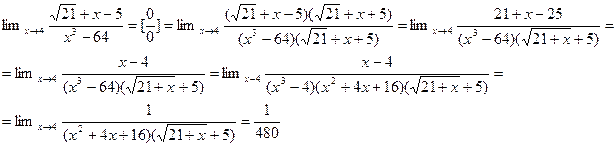
Задание 6. Найти предел функции 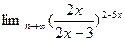
Решение: Имеем неопределенность вида 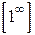 . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом 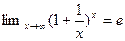 .
.
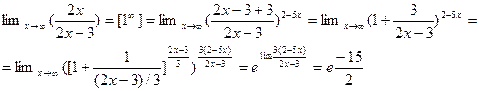
Производная и ее приложения .
По данной теме следует сначала изучить Глава VI [1], Глава V[3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
О: Производной функции y = f ( x )по аргументу х называется предел отношения приращения D у к приращению D х аргумента х, когда приращение аргумента стремиться к нулю:
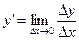
Дата: 2019-11-01, просмотров: 334.