Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

С’ = 0, где С – некоторое число

 

( u ± v)’ = u’ ± v’

 

(u*v)’ = u’v+v’u

 

 

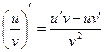
( Cx)’ = C

 

Дифференцирование основных элементарных функций.

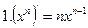
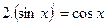
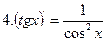
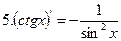
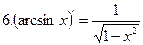
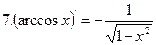
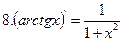
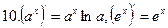
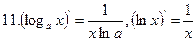
Пример: Найти производные следующих функций :

; ; ;

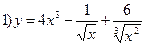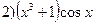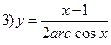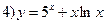
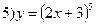
Решение. 1) Запишем данную функцию следующим образом:

.

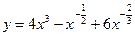Тогда

 

 

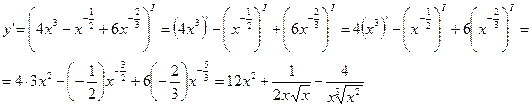
Имеем

 

 

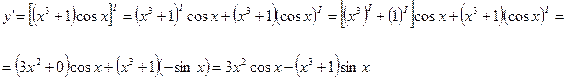
3) Имеем

 

 

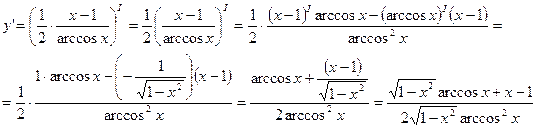
4) Имеем

 

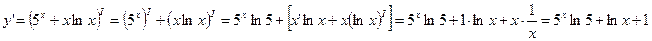
5) Имеем

 

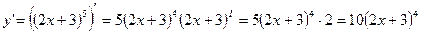
Дифференцирование сложных функций.

Примеры:

·

 

·

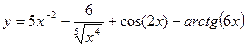
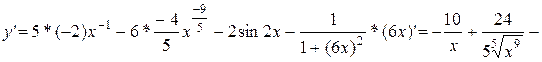
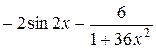
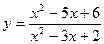
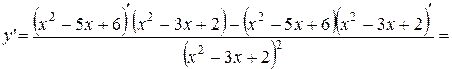
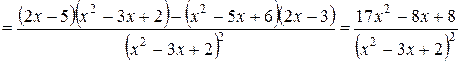
· у = (2х² –3х +4) (х² +5х +2)

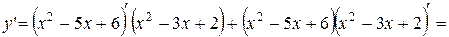
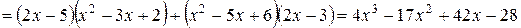
· у = ln (5x) +6^x + e ^2x

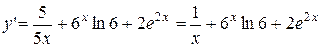
Вторая производная.

 

Примеры:

· У= 5х³ + 4х ^–2 - 8х + 4

Y’ = 15x² – 8x ^–3 – 8

Y’’= 30x + 24x ^–4

· У= cos³ x + x⁷ – e ^–4x

Y’ = 3cos²x(-sin x) + 7x⁶ +4e ^–4x

Y’’ = 6cosx (-sin x) (-sin x) - 3cos²x cos x +42x⁵ -16e ^–4x = 6cosx sin ²x - 3cos³ x +42x⁵ -16e ^–4x

 

Интегральное исчисление

Определение 1. Функция F ( x ) называется первообразной для функции f ( x ) в промежутке 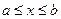, если в любой точке этого промежутка ее производная равна f ( x ):

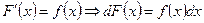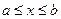, . (1)

Определение 2. Совокупность всех первообразных функций F(x) + с для функции f ( x ) на некотором промежутке называется неопределённым интегралом и обозначается

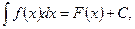 (2)

где f ( x ) dx называется подынтегральным выражением, х - переменной интегрирования, а С -произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например 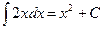, т.к.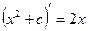

 

1. Метод непосредственного интегрирования.

Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводятся к одному или нескольким табличным интегралам.

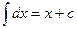
1.	9.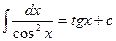
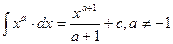
2.	10. =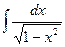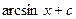
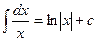
3.	11.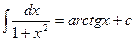
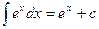
4.	12.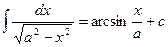
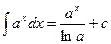
5.	13.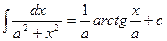
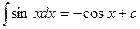
6.	14.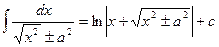
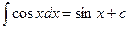
7.	15.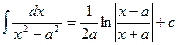
8.

 

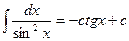
Примечание. Формулы верны, когда х является независимой переменной, а также когда х является функцией другой переменной: х=х(t).

Свойства неопределённого интеграла

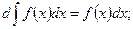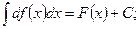1)   2) 3)

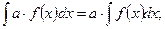
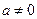
4)

 

 

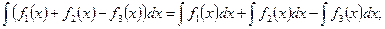
Примеры

 

1)

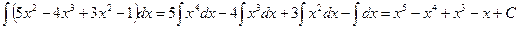
2)

 

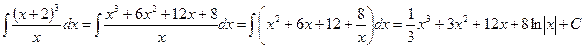
Интегрирование способом подстановки

Сущность интегрирования методом подстановки заключается в преобразовании интеграла 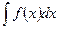 в интеграл 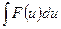, который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения  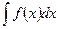заменяем переменную х новой переменной и с помощью подстановки. 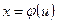.Дифференцируя это равенство, получаем 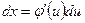. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через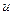 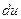, имеем

 

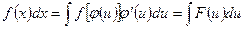            (3)

 

После того, как интеграл относительно новой переменной и будет найден, с помощью подстановки 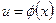 он приводится к переменной х.

 

Примеры:

l) 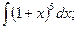     2)

 

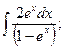
Решение:

1) положим 1 + х = z. Продифференцируем это неравенство: 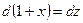 или dx = dz .

Заменим в интеграле: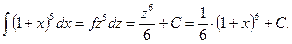

2) Сделав замену: 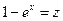, получим 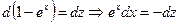. Тогда

 

 

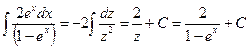
Вычисление о пределённого интеграла методом непосредственного интегрирования, подстановки.