Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется 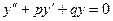 (1)

Для отыскания общего решения уравнения (1) составляется характеристическое уравнение r²+pr+q=0

Которое получается из уравнения (1) заменой в нём производных искомой функции с соответствующими степенями r, причём сама функция заменяется единицей. Тогда общее решение (1) строиться в зависимости от характера r₁ и r₂ уравнения (2).Здесь возможно 3 случая.

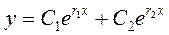1-случай.Корни r₁ и r₂-действительные и различные. Тогда общее решение уравнения (1) имеет вид

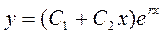2-случай. Корни r₁ и r₂-действительные и равные r₁₌r₂₌r.В этом случае общее уравнение (1) имеет вид 

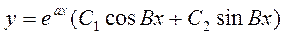3-случай. Корни r₁ и r₂-комплексно сопряжённые: r₁=a+Bi, r₂₌a-Bi. Тогда общее значение записывается так:

 

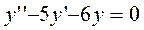Пример 1: Найти общее решение уравнения

Решение: Запишем характеристическое уравнение. Для этого заметим функцию y и её производные y’ и y” соответствующими степенями r: r⁰=1,r и r²

тогда получим r²-5r-6=0

откуда r₁=-1, r₂=6.

Т.к. корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения согласно 1 случая имеет вид

y=C₁e^-x+C₂e^6x.

 

Пример 2:Найти общее решение уравнения y”-4y’+4y=0

Решение: Составляем характеристическое уравнение r²-4r+4=0 из которого находим r_1,2=2. Характеристическое уравнение имеет равные действительные корни , поэтому согласно 2 случая общее решение запишется следующим образом:

y=e^2x(C₁+C₂x)

 

Пример 3 : Найти решение уравнения y”+9y=0

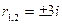Решение: Этому уравнению соответствует характеристическое уравнение r²+9=0 имеющее 2 мнимых сопряженных корня

Используя 3 случай при a=0 и b=3, получаем общее решение

y=C₁cos3x+C₂sin3x.

 

Пример 4:Найти общее решение уравнения y”+6y’+25y=0

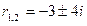Решение: Характеристическое уравнение r²+6r+25=0 имеет два комплексно сопряженных корня

Согласно 3 случая при a = -3 и b=4 получаем общее решение

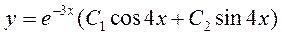Пример 5: Найти решение уравнения у”-3y’+2y=0 удовлетворяющее заданным начальным условиям y(0)=1, y’(0)=-1.

 

 Решение. Запишем характеристическое уравнение r² – 3r + 2 = 0; его корни r₁=1, r₂ = 2 Следовательно, общее решение имеет вид

y=C₁e^2x.

Далее, используя начальные условия, определяем значение постоянных C₁ и C₂. Для этого подставим в общее решение заданные значения x=0, y=1; В результате получим одно из уравнений, связывающее C₁ и С₂: 1= C ₁ + C ₂

Второе уравнение относительно C₁ и С₂ получим следующим образом. Продиффиринцируем общее решение y’= C₁e^2x+2С₂e^2x и подставим в найденное выражение заданные значения x=0, y’=-1: -1= C ₁ +2С₂

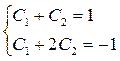Из системы

Находим C₁₌3, С₂₌-2. Следовательно, искомое частное решение имеет вид

y=3e^x-2e^2x