Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В пункте г) вашей контрольной работы предлагается взять интеграл от рациональной дроби.

Пример 15.

 

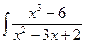
Под знаком интеграла стоит рациональная дробь.

1. Так как подинтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе),то выделим целую часть, разделив числитель на знаменатель “углом” (аналогично тому, как в задачах 41-50):

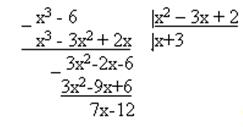
Итак, подынтегральную функцию можно записать в виде:

 

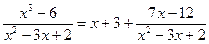
Тогда данный интеграл (обозначим его J), можно представить как сумму интегралов:

 

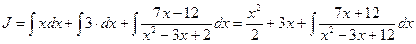
2. Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J₁, разложим знаменатель подынтегральной функции на множители.

Для этого найдем корни квадратного трехчлена, стоящего в знаменателе: x²-3x+12=0.

 

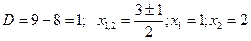
Тогда

 

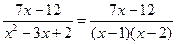
3. Представим полученную правильную дробь в виде суммы элементарных дробей:

4.            (*)

 

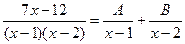Здесь А и В - числа, которые нужно найти. Сделаем приведение к общему знаменателю в правой части:

 

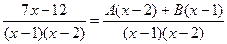
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:

7x-12=A(x-2)+B(x-1);

7x-12=Ax-2A+Bx-B;

7x-12=(A+B)x+(-2A-B).

Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х:

 

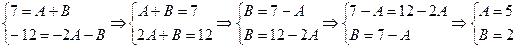
Получена система двух уравнений с двумя неизвестными А и В, решив которую, найдем А=5; В=2.

Подставим найденные числа в равенство (*):

 

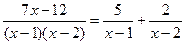
4. Вернемся к интегралу J₁:

 

 

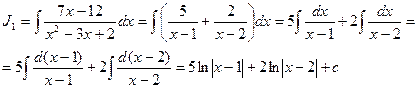
5. Окончательно искомый интеграл равен:

 

Вычисление площадей плоских фигур с помощью определённого интеграла.

Геометрический смысл определённого интеграла: площадь фигуры, ограниченной кривой у = f (х), где f (х) 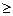0, осью ОХ и двумя прямыми х = а и х = b, выражается 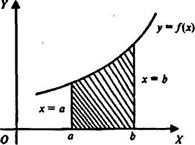определённым интегралом:  S =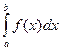  

Пример 1: определить площадь S фигуры, заключённой между ветвью кривой у = х², осью ОХ и прямыми х = 0, х = 3.

Решение: S =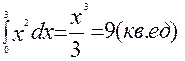

Пример 2: Найти площадь S фигуры, заключённой между осью ОХ и кривой у=х²-4х

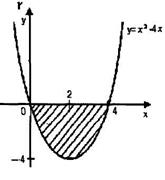
Решение: рассмотрим точки пересечения кривой у = х² - 4х с осью ОХ

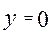
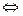х²-4х = 0  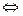 х(х-4) = 0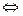 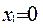 или х₂ = 4.

Найдём производную функции 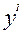 = 2х - 4 и точки экстремума:

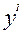 = 0 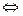2х-4 = 0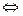^:  х = 2^: у" =2>0  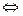х = 2 - точка min y(2) = - 4

Искомая площадь ограничена сверху OX, снизу y = х² – 4x, слева х = 0, справа

 х = 4. Так как у < 0, то

S= 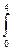(x² -4х)dх = 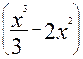= = 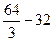 = = 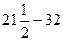 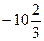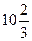(кв. ед.)

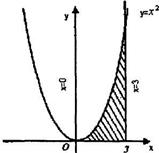
Пример 3: Найти площадь фигуры, заключённой между 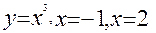и осью OX (рис.4 )

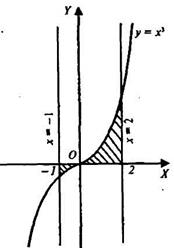
рис. 4

 

Найдем точки пересечения графика функции 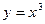 с осью абсцисс .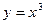

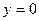
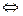
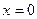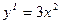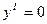
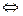
Точки экстремума: ; ; 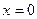; ; 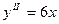;  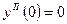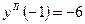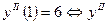меняет знак при переходе через х=0 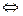т. (0;0) - точка перегиба. Значит, искомая площадь состоит из двух частей:

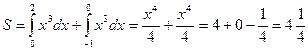 (кв.ед.)

Дифференциальные уравнения

 

Обыкновенным дифференциальным уравнением называется равенство, содержащее независимую переменную x, неизвестную функцию y и её производные :

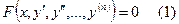
Порядок старшей производной уравнения (1) называется порядком уравнения. Решением уравнения (1) называется функция 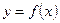, обращающая уравнение в тождество. Процесс нахождения решения называется интегрированием дифференциального уравнения. График решения на плоскости (x,y) называется интегральной кривой.

Например, функция 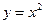 удовлетворяет уравнению  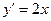и поэтому является его решением , однако это решение не единственно, т.к. семейство функций  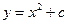, где 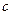– произвольная константа, также решение уравнения. Говорят, что функция (семейство функций)  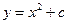является общим решением. Общее решение может быть найдено в явном, параметрическом или неявном виде, в любом случае оно должно зависеть от n констант 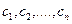. Если общее решение получено в неявном виде, то его часто называют общим интегралом уравнения.

Всякое решение, получающееся из общего при некоторых конкретных значениях констант, называется частным решением. Так, в рассмотренном примере 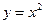 решение является частным, оно получается из общего при  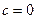Задачу нахождения частного решения в общей постановке можно сформулировать следующим образом:

найти частное решение уравнения (1) , удовлетворяющее условиям

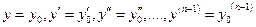(2)

Геометрически это означает, что интегральная кривая частного решения должна проходить через точку (x0,y0) и иметь заданные производные в этой точке, равные указанным значениям. Условия (2) называются начальными данными.

В общем случае не всякое решение получается из общего при конкретных (числовых) значениях констант. Решение, которое не содержится в общем решении ни при каких числовых значениях констант, называется особым решением.

При решении дифференциальных уравнений следует иметь в виду, что существуют типы уравнений, для которых известны шаблонные методы решения. Поэтому процесс решения разбивается, как правило, на три этапа:

1. Распознание типа решаемого уравнения либо приведение его к известному типу.

2. Применение известного шаблонного метода решения к распознанному уравнению.

3.  Интегрирование уравнения (взятие интегралов).

Первый этап - идеологический, требует навыка, опыта, набитие руки. Второй этап - справочный, требует хорошей памяти, умения запоминать. Третий этап - технический, требует владения техникой интегрирования (взятие неопределенных интегралов).

Учитывая, что 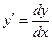, иногда дифференциальное уравнение записывают в дифференциалах. Например, уравнение  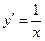   можно записать в виде .

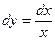Рассмотрим некоторые типы уравнений и методы их решения.

 

1. Простейшее дифференциальное уравнение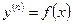

Интегрируя n раз обе части уравнения, найдем общее решение, зависящее от n констант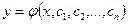

Пример 1 Найти частное решение уравнения 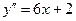 с начальными данными: при x=0 y=1, 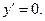Интегрируем дважды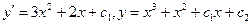

Из начальных условий следует: 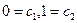. Таким образом,  .

 

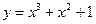2. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение y '= f ( x , y ) называется уравнением с разделяющимися переменными, если имеет следующий вид: 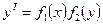                       (3)

В предположении, что f 2 ( y ) 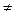0, уравнение с разделяющимися переменными (3) можно переписать в виде (разделить переменные):

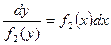            (4)

Уравнение вида (4) называется уравнением с разделёнными переменными.

При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться следующим алгоритмом:

1) разделить переменные (с учётом условий, когда это можно делать);

2) проинтегрировать почленно полученное уравнение с разделёнными переменными;

3) найти его общий интеграл;

4) выяснить, имеет ли уравнение (5) решения, не получающиеся из общего интеграла;

5) найти частный интеграл (или решение), удовлетворяющий начальным условиям (в случае задачи Коши).

 

Пример. Найти частное решение уравнения: 2у' = 1 - Зх2; у 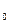 = 3 при х  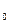= 0

 

Решение: это уравнение с разделяющимися переменными. Представим его в дифференциалах.

Учитывая, что 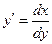получим 2у— = 1-3х .

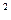Разделим переменные:

2 ydy = (1 - Зх2 ) dx . Интегрируя обе части последнего равенства, найдём

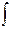2 ydy = 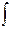(1 - Зх2 ) dx , т.е. у2=х-х3+С. Подставив начальные значения х0 =1, уо=3,найдём С: 9=1-1+С, т.е. С=9. Следовательно, искомый частный интеграл будет у2=х-х3+9, или х3+у2-х-9 = 0