Существует множество подходов к классификации текстовых задач. В рамках данной работы будут рассмотрены некоторые из них.

Л.М.Фридман классифицирует задачи следующим образом:

1) По характеру объекта.
Школьные задачи чаще всего различаются характером объектов. Если в задаче фигурируют реальные объекты – она называется практической, если объекты являются математическими (например, геометрическими фигурами), то задача называется математической.
Если для решения задачи существуют готовые правила решения, то такая задача называется стандартной. Если же для задачи нет общих правил, определяющих алгоритм решения, она нестандартная.

2) По характеру требований.
Такие задачи делятся на три класса: на нахождение искомого, на доказательство или объяснение, на преобразование или построение.

3) По отношению к теории.

Классификация Т.Е.Демидова и А.П.Тонких разделяет задачи по типу и виду, где тип задачи – это классификация по содержанию (задачи на движение, на части, на работу и т.д.). Внутри каждого типа задачи делятся по видам, в зависимости от структуры.

Есть и другая классификация задач:

1) По содержанию:

· Экономические:

o  Купля-продажа;

o  Оптимальный выбор;

o  Спрос-предложение.

· Физического содержания

· Задачи на прямую пропорциональную зависимость:

o  Движение;

o  Работа.

· Задачи на смеси/сплавы/растворы

2) По методу решения:

· Арифметические;

· Алгебраические (составление и решение уравнений и
 неравенств);

· Геометрические;

· Комбинированные.

3) По специфике языка:

· Текстовые;

· Сюжетные (в тексте задачи присутствует фабула);

· Абстрактные (предметные задачи).

Любая типология задач условна, и зависит от многих факторов. Например, одну и ту же задачу можно решить арифметически, алгебраически и геометрически. Отнесение задачи к тому или иному типу в данной ситуации зависит от того кто ее решает.

Методы решения текстовых задач

Решить математическую задачу – значит найти такую последовательность общих положений математики (определений, правил, аксиом и т.д.), применяя которые к условиям задачи или промежуточным результатам решения, получаем ответ за требование задачи.

Существует несколько методов решения текстовых задач:

1) Арифметический.
Решение сводится к поиску ответа на требование задачи, через выполнение арифметических действий над числами. Типы задач, для которых данным метод наиболее целесообразен: простые задачи, задачи на части/дроби.

2) Алгебраический.
Решение сводится к поиску ответа, через составление и решение уравнения, неравенства или их системы. Если для задачи можно составить несколько различных уравнений или систем, то целесообразно требовать от учеников искать все возможные способы решения. 

3) Геометрический.
Для решения задач геометрическим методом, необходимо проводить геометрические построения и/или использовать свойства различных геометрических фигур. Отличительной особенностью данного метода является его наглядность, которая помогает ученикам лучше вникнуть в условие.

4) Графический.
Л.М.Фридман отдельно выделяет этот метод. Для его использования ученикам достаточно знать график прямой пропорциональности. Решение таким методом сводится к построению графиков в прямоугольной системе координат.

5) Табличный.
Некоторые задачи быстрее и эффективнее решать через представление информации в виде таблицы. Данный метод достаточно наглядный и эффективный, он экономит много времени, которое обычно тратится на оформление и запись пояснений к действиям. Многие задачи можно решить «не выходя» из таблицы.

В школьном курсе математики есть задачи, решение которых возможно несколькими способами одновременно.

Этапы решения задач

Решение любой текстовой задачи осуществляется в четыре этапа:

1) Анализ условий и требования.
На этом этапе ученик должен прочитать и осмыслить текст задачи и ситуацию, которую она описывает. Анализ можно проводить по двум направлениями: предметно-содержательному (мысленное воссоздание заданной ситуации) или логико-семантическому (разбиение задачи на элементарные условия, установление величин и соотношений между ними, т.е. выделение структуры задачи). Для оформления результатов анализа используются схематические записи, т.е. вспомогательные модели, помогающие в переводе текста задачи на математический язык. Они могут быть представлены в виде схем, таблиц, чертежа, рисунка и т.п.

2) Построение плана решения задачи.
На этом этапе ученик устанавливает связи между данными и искомыми величинами, указывает последовательность использования этих связей. Есть два пути решения: от вопроса к данным (аналитический) или от данных к вопросу (синтетический). В.А.Далингер предлагает изображать разбор задачи от ее вопроса к условию в виде «дерева рассуждений». Построение такого «дерева» – анализ, а решение задачи по данной схеме – синтез.
Этот этап считается самым трудным для учащихся.

3) Осуществление плана решения задачи.
На этом этапе ученик реализует ранее составленный план и таким образом находит ответ на требование задачи. Большое внимание необходимо уделить записи решения и описанию промежуточных этапов.

4) Проверка решения.
После записи или озвучивания решения, необходимо проверить его правильность. Проверка может быть прямой или косвенной, и каждая из них может быть полной (выполнение всех условий задачи) или частичной (выполнение некоторых условий задачи). Косвенная проверка представляет собой составление и решение задачи, обратной данной. Так же косвенную проверку можно выполнить через решение исходной задачи другим способом.

Если ученик научится внимательно анализировать задачи, вдумчиво решать каждую из них, фиксируя в своей памяти все приёмы и способы, использованные для нахождения решения, то постепенно у него выработается умение решать любую задачу. Профессор Московского университета С.А.Яновская на вопрос «Что значит решить задачу?» дала короткий ответ: «Решить задачу – значит свести её к уже решённым».

При решении задач «на работу» используется следующий алгоритм:

1) При решении таких задач мы имеем дело с тремя параметрами:

· Время – t (время, за которое выполняется работа);

· Объем работы – А (объем работы, выполняемый за единицу времени);

· Производительность – P (скорость работы).

Эти три величины – пропорциональны и связаны между собой следующими формулами:

·

·

·

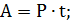
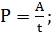
2) Содержание подобных задач обычно сводится к следующему: некоторую работу, объем которой не является искомым и не указывается, выполняют несколько объектов, работающих равномерно (т.е. с постоянной для каждого производительностью). Производительность и время – взаимообратные величины, т.е. вся работа по формуле равна единице. Следовательно, в таких задачах объем всей работы, которая должна быть выполнена, если он не указан, принимается за единицу.

3) Во время решения задач «на работу» необходимо ответить на следующие вопросы:

· Что принято за время выполнения работы первым/вторым/и т.д. рабочим?

· Какова производительность труда первого/второго/и т.д. рабочего?

· Чему равно время, за которое будет выполнен работа?

· Эффективность какого рабочего выше?

Ответить на эти вопросы можно как в виде составления математической модели, так и с помощью таблицы.