Задание № 31-40. Найти производную функции
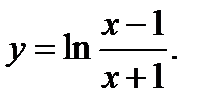
31.
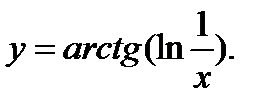
32.
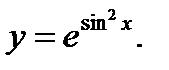
33.
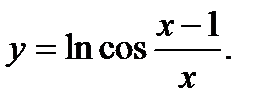
34.

35.
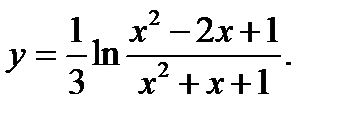
36.
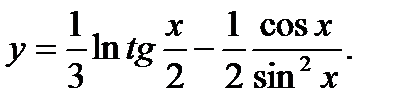
37.
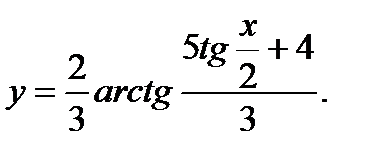
38.
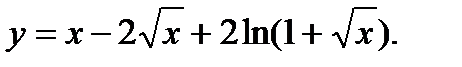
39.
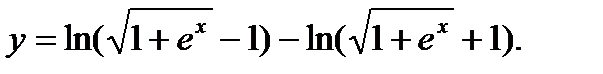
40.
Задания №41-50. Исследовать функцию и построить её график
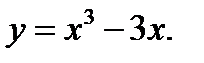
41.
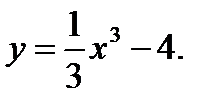
42.
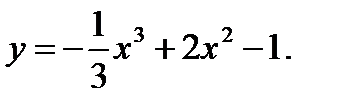
43.
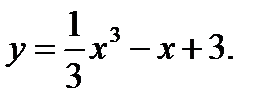
44.
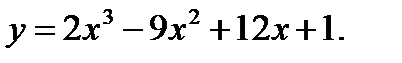
45.
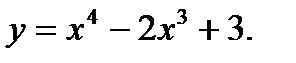
46.
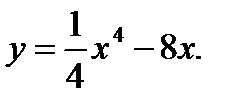
47.
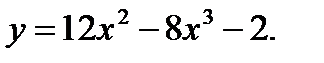
48.
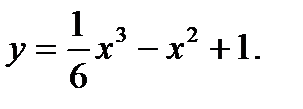
49.
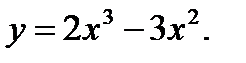
50.
Задание №51-60. Вычислить определённый интеграл
| 51. | 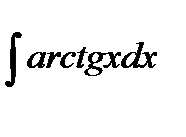 а) а)
| 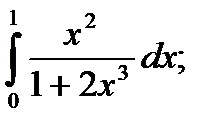 б) б)
|
| 52. | 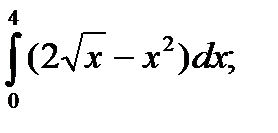 а) а)
| 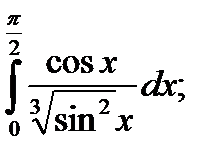 б) б)
|
| 53. | 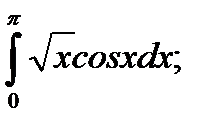 а) а)
| 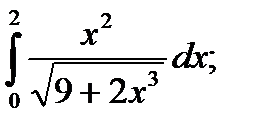 б) б)
|
| 54. | 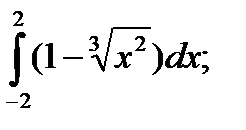 а) а)
| 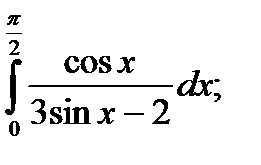 б) б)
|
| 55. | 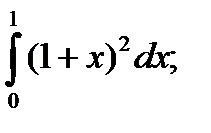 а) а)
| 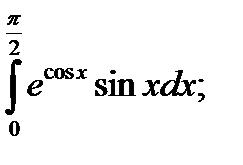 б) б)
|
| 56. | 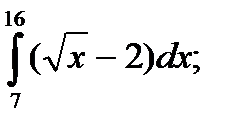 а) а)
| 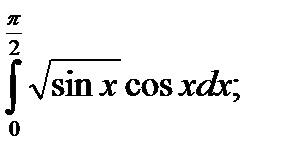 б) б)
|
| 57. | 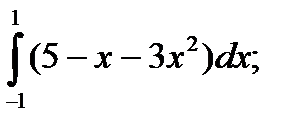 а) а)
| 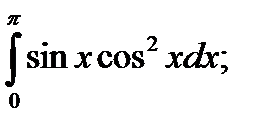 б) б)
|
| 58. | 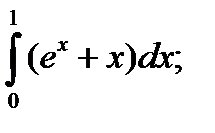 а) а)
| 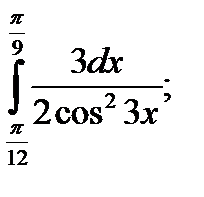 б) б)
|
| 59. | 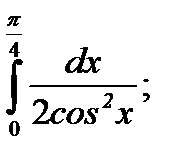 а) а)
| 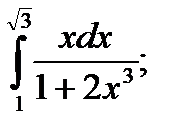 б) б)
|
| 60. | 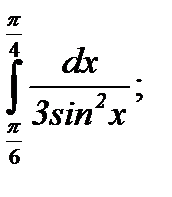 а) а)
| 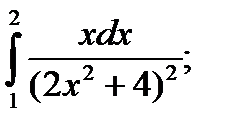 б) б)
|
Задание №61-70. Вычислить площадь фигуры, ограниченной линиями
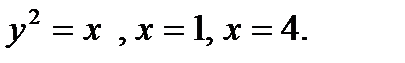
61.
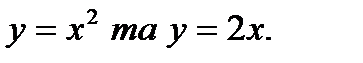
62.
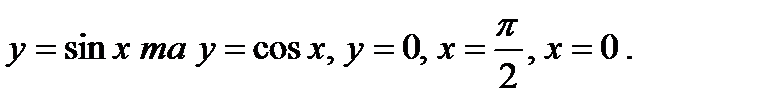
63.
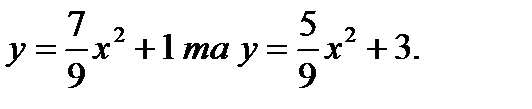
64.
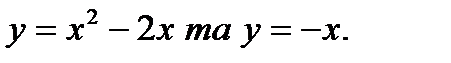
65.
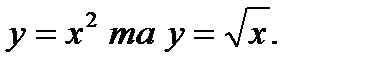
66.
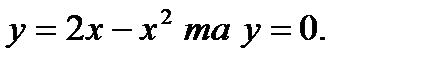
67.
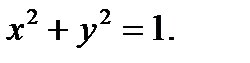
68.
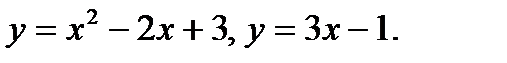
69.
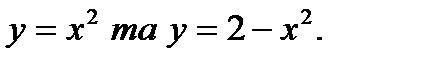
70.
Тема: Элементы математической статистики
Задание № 71-80. Задачи на классическое определение вероятности, применение формул комбинаторики для вычисления вероятности
Задание 71.
Какова вероятность того, что при бросании игрального кубика выпадает чётное число очков?
Задание 72.
В одном ящике находятся 8 белых и 12 красных шариков, в другом – 15 синих и 5 чёрных шариков. Из каждого ящика наугад вынимают по одному шарику, какова вероятность того, что вынули красный и чёрный шарики?
Задание 73.
В ящике лежат 20 одинаковых на ощупь шариков. Из них 12 белых и 8 чёрных. Наугад вынимают два шарика. Какова вероятность того, что оба шарика белые? Что они разного цвета?
Задание 74.
Из ящика, в котором находятся 4 шарика, пронумерованные числами 0, 1, 2, 3, наугад берут два шарика. Составить закон распределения суммы номеров двух вынутых шариков.
Задание 75.
При сборке прибора для точной подгонки определённой детали необходимо сделать несколько попыток. При этом деталь, забракованная при сборке одного прибора, уже используется при сборке других. Для установления количества деталей, которыми необходимо обеспечить рабочего, было проведено 100 наблюдений. Оказалось, что в 7 случаях понадобилась одна попытка, в 16 – две, в 55 – три, в 21 – четыре и в одном случае – пять попыток. Найти среднее количество деталей, необходимых для сборки одного прибора.
Задание 76.
Найти математическое ожидание Х, равной числу очков, которые выпадают на игральном кубике при одном броске.
Задание 77.
Подбросили два игральных кубика и подсчитали сумму выпавших очков. Что вероятнее получить в сумме: 7 или 8?
Задание 78.
В корзине находятся 4 белых и 7 чёрных шариков. Какова вероятность того, что наугад вынутый шарик окажется белого цвета?
Задание 79.
Подбросили две монеты. Какова вероятность того, что на каждой монете выпадет герб?
Задание 80.
Из полного набора костей домино наугад выбирается одна кость. Какова вероятность появления кости, сумма очков на которой равна шести?
Литература
Основная
1 Богомолов Н.В., Самойленко П.И. Математика. – М.: Дрофа, 2010.
2 Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика: Підручник. – К.: Вища школа., 2005
3 Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики: Навчальний посібник. – К.: Вища школа., 2005
4 Голованов Н.Н. Геометрическое моделирование. Учебник., М.: ФИЗМАТЛИТ, 2002
5 Валєєв К.Г., Джалладова І.А. Вища математика: Навч. посібник. У 2-х ч - К.: КНЕУ, 2001
6 Лопатько О.В. Математичні методи в розрахунках на ЕОМ: Навчальний посібник. – Львів: «Магнолія плюс», 2005
Дополнительная
1 В.М.Лейфура. Математика: Учебник для высших учебных учреждений І-ІІ уровней аккредитации – К.: Техника, 2003
2 Яковлев Г.М. Алгебра и начало анализа. Учебник ч І-ІІ - М.: Наука, 1987
3 Крамор в.С., Алгебра и начала анализа: Учебное пособие для вузов. – М.: Высшая школа, 2001.
4 Валуце І.І. Математика для техникумов. Учебник. – М.: Наука, 1987
5 Богомолов М.В. Практичні заняття з математики. Навчальний посібник. – К.: Вища школа, 1987
6 Зайцев И.Л. Элементы высшей математики для техникумов. Учебник. – М.: «Наука», 1982
Дата: 2019-11-01, просмотров: 334.