Напомним, что дифференциал функции 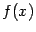 (называемый также первым дифференциалом, или дифференциалом первого порядка) задаётся формулой
(называемый также первым дифференциалом, или дифференциалом первого порядка) задаётся формулой
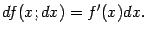
Рассмотрим это выражение (при фиксированном приращении 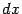 аргумента
аргумента  ) как функцию переменного
) как функцию переменного  и найдём её дифференциал
и найдём её дифференциал 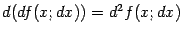 :
:
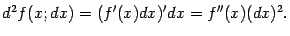
Этот дифференциал от первого дифференциала называется вторым дифференциалом от функции 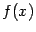 , или дифференциалом второго порядка. Аналогично, дифференциал от второго дифференциала называется третьим дифференциалом; он задаётся формулой
, или дифференциалом второго порядка. Аналогично, дифференциал от второго дифференциала называется третьим дифференциалом; он задаётся формулой
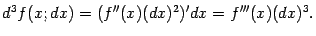
Вообще, 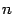 -й дифференциал
-й дифференциал 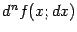 , или дифференциал
, или дифференциал 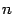 -го порядка, определяется как дифференциал от
-го порядка, определяется как дифференциал от 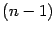 -го дифференциала (при постоянном приращении
-го дифференциала (при постоянном приращении 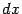 ); для него имеет место формула:
); для него имеет место формула:
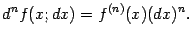
Практическое занятие. Нахождение неопределённого интеграла
Цель. Формирование умений и навыков вычисления неопределённого интеграла непосредственным интегрированием, методами интегрирования по частям и заменой переменной.
Неопределённый интеграл и таблица неопределённых интегралов
Определение Пусть 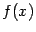 - функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для
- функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для 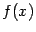 называется неопределённым интегралом от
называется неопределённым интегралом от 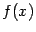 и обозначается
и обозначается 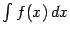 . Операция нахождения неопределённого интеграла по заданной функции
. Операция нахождения неопределённого интеграла по заданной функции 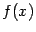 называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функция
называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функция 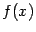 , записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией.
, записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией.
Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции 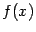 состоит из функций вида
состоит из функций вида 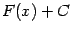 , где
, где 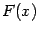 -- какая-либо фиксированная первообразная для
-- какая-либо фиксированная первообразная для 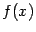 , а
, а 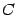 -- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция
-- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция 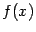 . Поэтому можно написать такую формулу:
. Поэтому можно написать такую формулу:
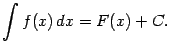
(Точнее было бы 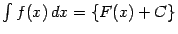 , но фигурные скобки, обозначающие множество всех функций вида
, но фигурные скобки, обозначающие множество всех функций вида 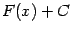 , писать в данной ситуации не принято.)
, писать в данной ситуации не принято.)
Итак, для того чтобы доказать равенство 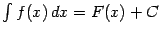 , достаточно проверить, что
, достаточно проверить, что 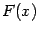 -- первообразная для
-- первообразная для 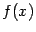 , то есть что
, то есть что 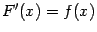 .
.
| 1 | 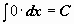 . .
| 11 | 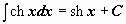 . .
|
| 2 | 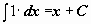 . .
| 12 | 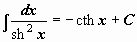 . .
|
| 3 | 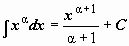 ( ( 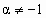 ). ).
| 13 | 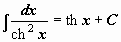 . .
|
| 4 | 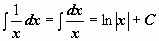 . .
| 14 | 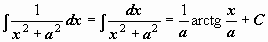 . .
|
| 5 | 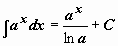 ; ;  . .
| 15 | 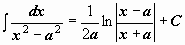 . .
|
| 6 | 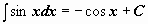 . .
| 16 | 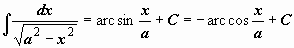
|
| 7 | 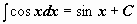 . .
| 17 | 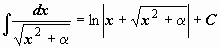 . .
|
| 8 |  . .
| 18 | 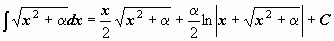 . .
|
| 9 | 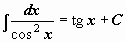 . .
| 19 |  . .
|
| 10 |  . .
| 20 | 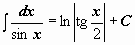 ; ; 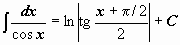 . .
|
Интегрирование по частям
 Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du
Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du 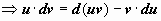 . Находим неопределённые интегралы для обеих частей этого равенства (при этом
. Находим неопределённые интегралы для обеих частей этого равенства (при этом 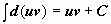 ):
):


 .
.
 Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙ dx , du = u’∙ dx):
Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙ dx , du = u’∙ dx):
 .
.
 Примеры:
Примеры: 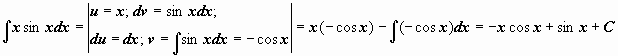 .
. 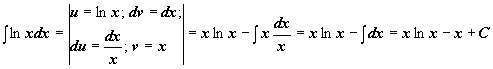 .
.
 Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде
Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде 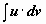 :
: 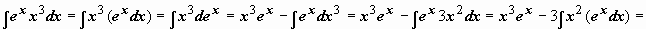
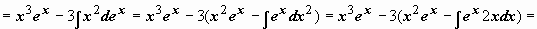

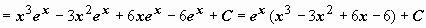 .
.
 Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:
Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:
 Интегралы вида
Интегралы вида 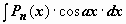 ,
, 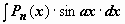 ,
,  , где Pn(x) - многочлен n-ой степени. Так, для
, где Pn(x) - многочлен n-ой степени. Так, для 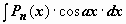 имеем
имеем  ,
, 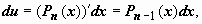
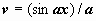 , и
, и  . В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.
. В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.
 Интегралы
Интегралы 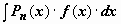 , где
, где 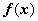 - трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = Pn(x)dx, для того, чтобы в интеграле
- трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = Pn(x)dx, для того, чтобы в интеграле 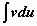 участвовала не f(x), а её производная. Пример:
участвовала не f(x), а её производная. Пример: 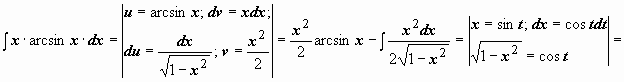
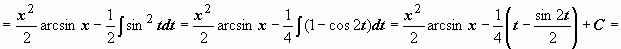
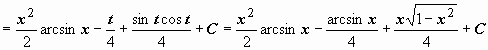 .
.
 Для некоторых функций применяется приём “сведения интеграла к самому себе”. С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла. Примеры:
Для некоторых функций применяется приём “сведения интеграла к самому себе”. С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла. Примеры:
 Найти
Найти 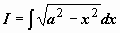 (это интеграл №19 из табл. 10.3.неопределённых интегралов; в предыдущем параграфе мы вычислили этот интеграл с помощью тригонометрической подстановки
(это интеграл №19 из табл. 10.3.неопределённых интегралов; в предыдущем параграфе мы вычислили этот интеграл с помощью тригонометрической подстановки 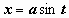 ).
). 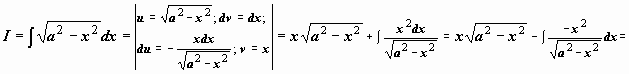
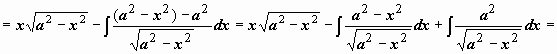
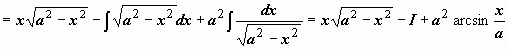 .
.
 В результате для искомого интеграла мы получили уравнение
В результате для искомого интеграла мы получили уравнение 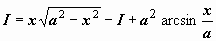 ,
,
решая которое, получаем 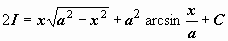 (константа С появилась вследствие того, что интегралы
(константа С появилась вследствие того, что интегралы 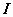 в правой и левой частях уравнения определены с точностью до произвольной постоянной) и
в правой и левой частях уравнения определены с точностью до произвольной постоянной) и 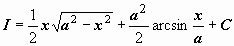 (константа
(константа 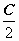 переобозначена через С).
переобозначена через С).
 Сведение интеграла к самому себе – самый простой способ нахождения часто встречающихся интегралов вида
Сведение интеграла к самому себе – самый простой способ нахождения часто встречающихся интегралов вида 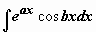 и
и 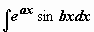 (
( 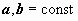 ). Например,
). Например,
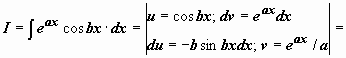
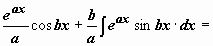
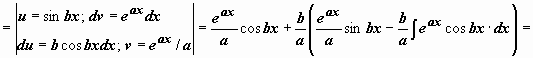
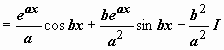 . Итак, после двукратного интегрирования по частям получено уравнение относительно
. Итак, после двукратного интегрирования по частям получено уравнение относительно 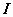 :
: 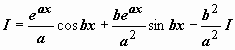 , решение которого
, решение которого  .
.
 При нахождении эти интегралов не принципиально, положим ли мы u = cos bx, dv = eax dx или u = eax, dv = cos bx dx; важно только при втором применении формулы интегрирования по частям загонять под знак дифференциала функцию того же типа, что и при первом (показательную или тригонометрическую).
При нахождении эти интегралов не принципиально, положим ли мы u = cos bx, dv = eax dx или u = eax, dv = cos bx dx; важно только при втором применении формулы интегрирования по частям загонять под знак дифференциала функцию того же типа, что и при первом (показательную или тригонометрическую).
Ещё один вид формул, которые обычно получаются с помощью интегрирования по частям, и используются для нахождения интегралов - рекуррентные соотношения. Если подынтегральная функция зависит от некоторого параметра n, и получено соотношение, которое выражает интеграл через аналогичный интеграл с меньшим значением n, то это соотношение и называется рекуррентным соотношением.
Примеры:
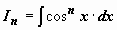 . Представим подынтегральную функцию в виде
. Представим подынтегральную функцию в виде 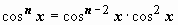
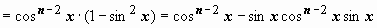 ; интеграл от первого слагаемого аналогичен исходному с значением параметра n на две единицы меньше; к интегралу от второго слагаемого применим формулу интегрирования по частям:
; интеграл от первого слагаемого аналогичен исходному с значением параметра n на две единицы меньше; к интегралу от второго слагаемого применим формулу интегрирования по частям:
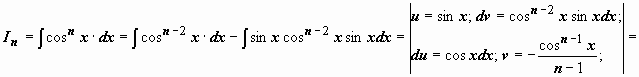
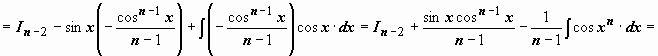
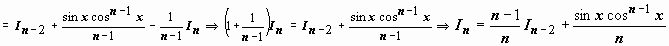 .
.
 Теперь, зная
Теперь, зная  ,
, 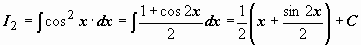 , мы можем выписать
, мы можем выписать 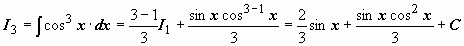 ;
; 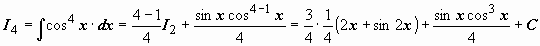 ;
;
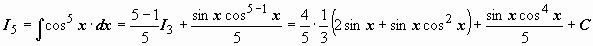

Практическое занятие. Вычисление определённого интеграла
Дата: 2019-11-01, просмотров: 335.