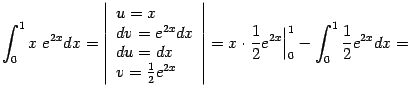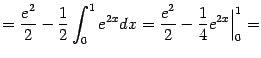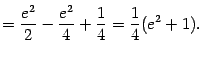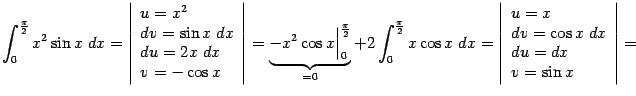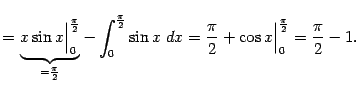Теорема . Пусть функции 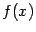 и
и 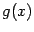 имеют на отрезке
имеют на отрезке  непрерывные производные
непрерывные производные 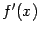 и
и 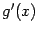 . Тогда имеет место формула
. Тогда имеет место формула
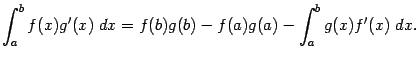
Замечание. Заметим, что эту формулу можно записать в виде
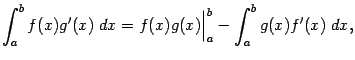
где выражение
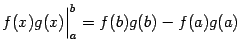
называется внеинтегральным членом. Введя обозначения 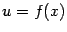 и
и 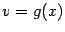 , мы можем переписать формулу интегрирования по частям в более коротком виде:
, мы можем переписать формулу интегрирования по частям в более коротком виде:
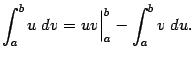
Пример 2. Вычислим интеграл
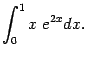
Выгодно взять 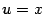 и
и 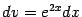 , так что получаем:
, так что получаем:
|
|
|
|
|
|
|
|
|
При этом возникший по дороге внеинтегральный член 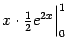 мы вычислили так:
мы вычислили так:
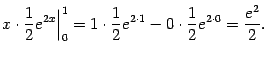
Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд.
Пример 3. Вычислим интеграл
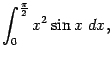
применив формулу интегрирования по частям два раза подряд. Имеем:
|
|
|
|
|
|
Если бы мы сразу же не вычисляли значения подстановок во внеинтегральных членах, то нам пришлось бы несколько раз при нахождении первообразных выписывать значения этих внеинтегральных членов  и
и  , а здесь мы сразу же заменили первую подстановку на 0, а вторую на
, а здесь мы сразу же заменили первую подстановку на 0, а вторую на 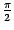 , что сэкономило некоторое место в записи и наши усилия.
, что сэкономило некоторое место в записи и наши усилия.
Практическое занятие. Вычисление площади криволинейной трапеции и объёмов тел вращения с помощью определённого интеграла.
Цель работы: совершенствовать умения вычислять определенные итегралы, находить площадь криволинейной трапеции, решать задачи, применять интегрирование к решению задач.
Геометрический смысл определенного интеграла:
Определённый интеграл численно равен площади криволинейной трапеции, ограниченной прямыми х=а; х=b; у=0 и частью графика функции 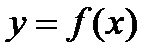 , взятой со знаком плюс, если функция положительна, и со знаком минус, если функция отрицательна (рисунок 1)
, взятой со знаком плюс, если функция положительна, и со знаком минус, если функция отрицательна (рисунок 1)
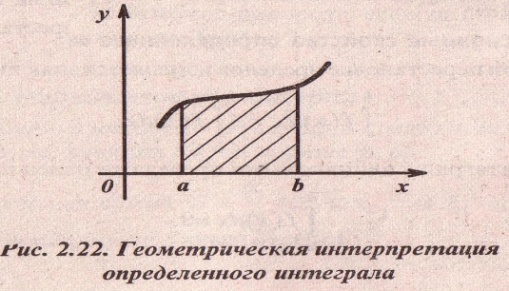
Основные случаи расположения плоской фигуры
| 1 | 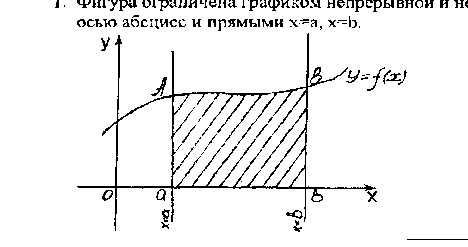
| 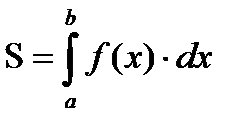
|
| 2 | 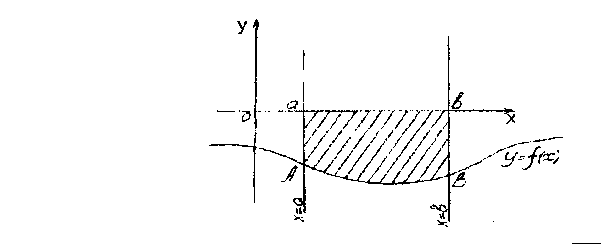
| 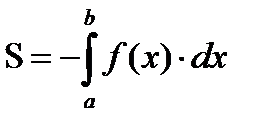
|
| 3 | 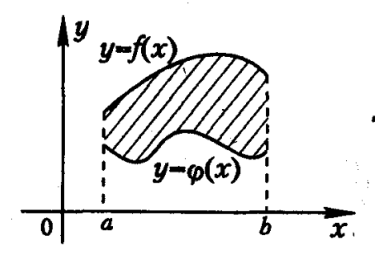
| 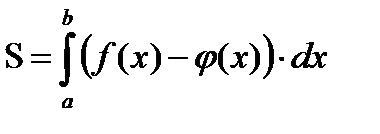
|
Пример1 . Найти площадь фигуры, заключённой между линиями y = x 3 , x = -1. x = 2 и осью OX
Решение: найдем точки пересечения графика функции 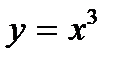 с осью ОХ(см. рис 4):
с осью ОХ(см. рис 4):
y = x 3; y = 0  x = 0; Вычислим производную функции: y ’ = 3 x 2; y ’ = 0
x = 0; Вычислим производную функции: y ’ = 3 x 2; y ’ = 0  x = 0 . Найдем значение второй производной в точке х=0: y ” = 6 x ; y ” (0) = 0. Вычислим y ”(-1) = -=6; y ”(1) = 6;
x = 0 . Найдем значение второй производной в точке х=0: y ” = 6 x ; y ” (0) = 0. Вычислим y ”(-1) = -=6; y ”(1) = 6;  Т.к. y ” меняет знак при переходе через х =0
Т.к. y ” меняет знак при переходе через х =0  т. (0;0) – точка перегиба. Искомая площадь состоит из двух частей, поэтому:
т. (0;0) – точка перегиба. Искомая площадь состоит из двух частей, поэтому:
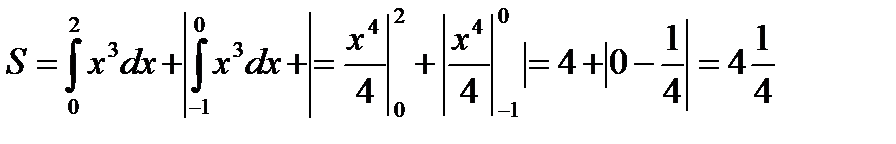 (кв.ед.)
(кв.ед.)
Физические приложения интеграла
| Величины | Вычисление производной | Вычисление интеграла |
| А – работа; F – сила; N - мощность. | F(x)=A' (x); N(t)=A' (t). | A= 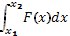 ;
A= ;
A= 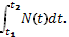
|
| m –масса тонкого стержня p – линейная плотность | P(x)=m' (x). | m= 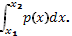
|
| Q –электрический заряд; I – сила тока. | I(t)=q' (t) | Q= 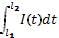
|
| S –перемещение; v –скорость. | V(t)=S' (t) | S= 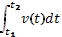
|
| Q –количество теплоты; с – теплоёмкость. | C(t)=Q' (t) | Q= 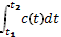
|
Пример 2 Дано ускорение скорости движения тела 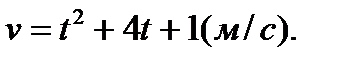 . Найти путь тела, за первые 3 с .
. Найти путь тела, за первые 3 с .
Решение:
Уравнение пути s(t) находится интегрированием:
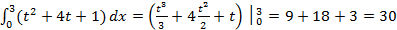 ( м)
( м)
Задания для практической работы
Задание 3. Вычислить определенные интегралы
а) 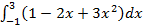 б)
б) 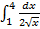 в)
в) 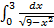
Задание 4. Вычислить определенные интегралы методом подстановки.
а) 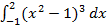
б). 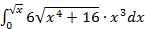
в) 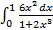
Задание 5. Вычислить площадь фигуры ограниченной линиями
1. 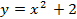
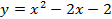
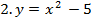
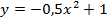
Задание 6. Решить задачу.
1.Скорость точки задана уравнением 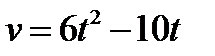 (м/с). Найти её путь за третью секунду движения.
(м/с). Найти её путь за третью секунду движения.
2.Скорость точки задана уравнением 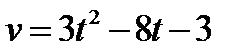 (м/с). Найти путь, пройденный телом за время от начала движения до остановки.
(м/с). Найти путь, пройденный телом за время от начала движения до остановки.
5. Методические рекомендации по выполнению и оформлению домашней контрольной работы
Контрольная работа по учебной дисциплине «Математика» для студентов заочной формы обучения составлена согласно учебному плану основной профессиональной образовательной программы среднего профессионального образования Государственного профессионального образовательного учреждения ГПОУ «Донецкий горный техникум им. Е.Т. Абакумова» по специальности
46.02.01 «Документационное обеспечение управления и архивоведение»
Задания контрольной работы охватывают все основные темы учебной программы. Контрольная работа выполняется студентом в тетради, где указывается номер варианта (задания студент выбирает из таблицы вариантов своей учебной группы), код (номера заданий, соответствующие варианту). Студент пользуется методическими указаниями для выполнения контрольной работы и указанной литературой, конспектом. Если студент применяет дополнительную литературу не указанную в списке, то необходимо в конце работы указать используемые источники, интернет-ресурсы и т.д.
Титульный лист заполняется согласно методическим требованиям, с которыми студент знакомится на установочной сессии.
Контрольная работа считается выполненной (выставляется оценка «зачтено»), если студент правильно решил и оформил более 80 % заданий. В противном случае работа возвращается студенту на доработку. Студент должен представить контрольную работу на проверку преподавателю в указанный срок, согласно учебному плану. В противном случае студент получает оценку «неудовлетворительно» и обязан выполнить контрольную работу заново.
Студент имеет право получить консультацию у преподавателя по графику консультаций, с которым может ознакомиться на заочном отделении или выяснить у преподавателя.
ТАБЛИЦА ВАРИАНТОВ
для выполнения контрольной работы
по учебной дисциплине «Математика»
для студентов заочной формы обучения специальности 46.02.01
«Документационное обеспечение управления и архивоведение»
Преподаватель: Левченко В.А.
Группа: 1Д-17/з
| № варианта | ||||||||
Номера заданий
Примечание: номер варианта соответствует порядковому номеру ФИО студента контингента в журнале успеваемости.
Тема: Функции, область определения функции, предел функции
Задания 1-10. Найти область определения функции
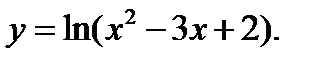
1.
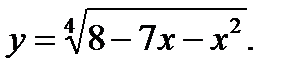
2.
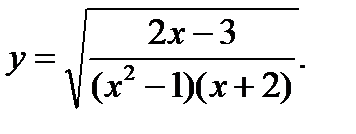
3.
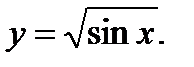
4.
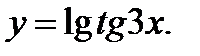
5.
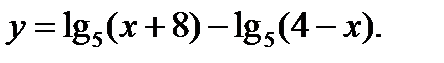
6.
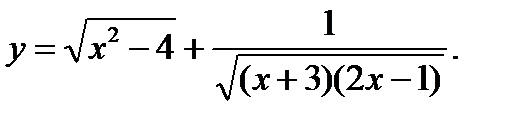
7.
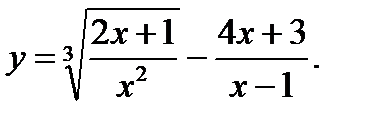
8.
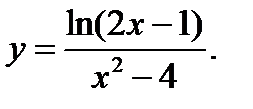
9.
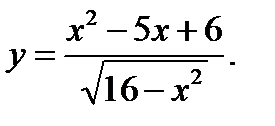
10.
Задания № 11-20. Найти предел функции
| 11. | 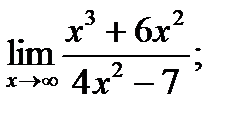 а) а)
| 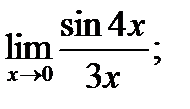 б) б)
|
| 12. |  а) а)
| 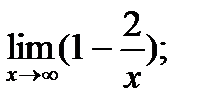 б) б)
|
| 13. | 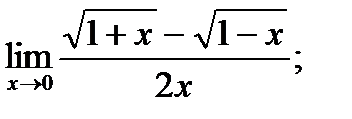 а) а)
| 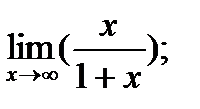 б) б)
|
| 14. | 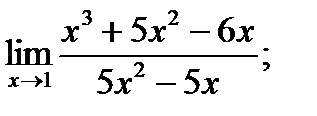 а) а)
| 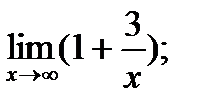 б) б)
|
| 15. | 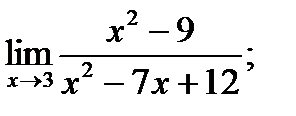 а) а)
| 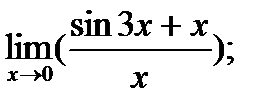 б) б)
|
| 16. | 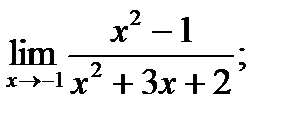 а) а)
| 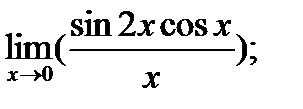 б) б)
|
| 17. | 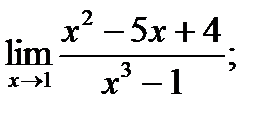 а) а)
| 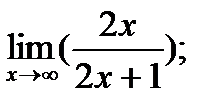 б) б)
|
| 18. | 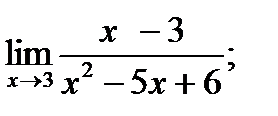 а) а)
| 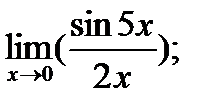 б) б)
|
| 19. | 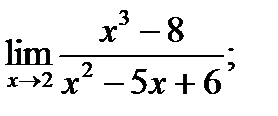 а) а)
| 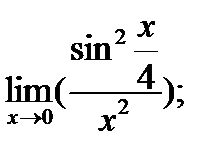 б) б)
|
| 20. | 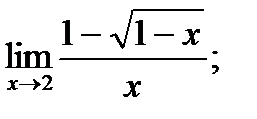 а) а)
| 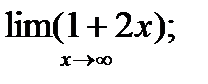 б) б)
|
Тема: Метод координат
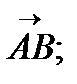 Задания № 21-30. В треугольнике с вершинами А(х1,, у1), В(х2,, у2) та С(х3, у3) найти:
Задания № 21-30. В треугольнике с вершинами А(х1,, у1), В(х2,, у2) та С(х3, у3) найти:
а) длину вектора
б) косинус внутреннего угла 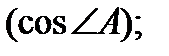
в) уравнение высоты, проведённой через вершину С;
г) уравнение медианы, которая проходит через вершину С;
д) выполнить рисунок.
21. А(0; 0) В(6; 3) С(3; 4)
22. А(1; -3) В(-5; 0) С(-2; 1)
23. А(-1; 1) В(5; 4) С(2; 5)
24. А(0; 0) В(6; 3) С(3; 4)
25. А(2; 2) В(-4; 5) С(-1; 6)
26. А(-1; -2) В(5; 1) С(2; 2)
27. А(-2; -1) В(4; 2) С(1; 3)
28. А(2; -1) В(-8; 4) С(-5; 5)
29. А(-1; -1) В(-7; 2) С(-4; 3)
30. А(3; -1) В(-3; 2) С(0; 3)
Дата: 2019-11-01, просмотров: 344.