(ДОК 1) Формула Грина. Пусть в области 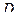, граница которого - замкнутый контур 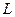, являющийся односвязным множеством, задано плоское векторное поле .

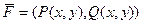Тогда верна такая формула: .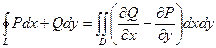

(ДОК 2) Криволинейный интеграл 2 рода не зависит от пути 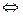 циркуляция по замкнутому контуру равна 0.

(ДОК 3) Поле F потенциально 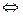криволинейный интеграл 2 рода от F не зависит от пути, причём тогда потенциал в любой точке  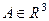вычисляется в виде  .

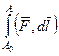(ДОК 4) 1) Если поле 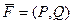 потенциально то симметрична производная матрица .

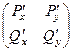2) Если граница области D, в которой задано векторное поле, является односвязным множеством, и симметрична производная матрица 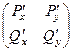, то поле потенциально.

 (ДОК 5) Действительную и мнимую часть 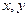 для числа  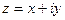можно выразить через . ,

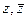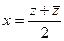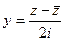
(ДОК 6) Формула Эйлера .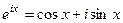

(ДОК 7) , .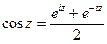

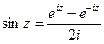(ДОК 8) .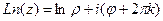

(ДОК 9). Доказать что линейное отображение 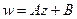 в комплексной плоскости есть композиция растяжения, поворота и сдвига.

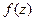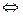
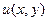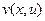(ДОК 10) Функция  дифференцируема  и  дифференцируемы и выполняются условия Коши-Римана:

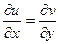 и .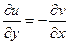

(ДОК 11) 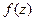 дифференцируемая функция  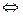векторные поля

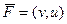 и 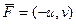 являются потенциальными.

(ДОК 12) Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой) 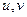 в этой области выполняется уравнение Лапласа:  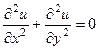и .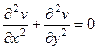

(ДОК 13) Условия Коши-Римана эквивалентны условию .

(ДОК 14). Докажите, что если 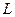 замкнутый контур, внутри которого во всех точках  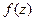является аналитической, то .

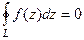(ДОК 15). Докажите, что если 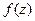 является аналитической во всех точках некоторой области 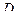, граница которой односвязна, то интеграл от функции  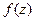не зависит от пути, то есть имеет одно и то же значение для любой кривой 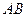, соединяющей пару точек .

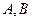(ДОК 16). Докажите, что функция 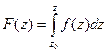 является первообразной от функции .

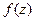(ДОК 17). Докажите, что для аналитической на кривой 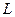 функции верна формула Ньютона-Лейбница: .

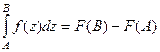(ДОК 18). Доказать интегральную теорему Коши о том, что .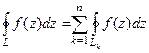

(ДОК 19). Доказать интегральную формулу Коши: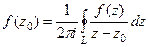

(ДОК 20) (Обобщённая интегральная формула Коши).

Пусть 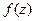 является аналитической на контуре  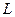и внутри него, точка  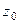лежит внутри 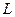. Тогда .

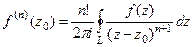(ДОК 21) Лемма Доказать, что 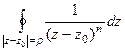 = 0 для любого целого .

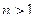(ДОК 22) Если 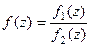, причём точка  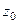является нулём порядка m для функции 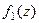, и нулём порядка n для функции 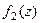, то при  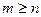точка 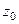 устранимая или правильная точка, а при  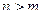полюс порядка  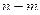для функции .

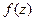(ДОК 23) Если 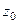 простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета:  = .

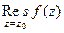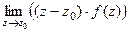(ДОК 24) Если 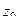 - полюс порядка m,  то верна формула вычисления вычета:  = .

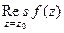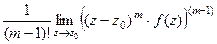Литература

1. Л.И.Магазинников. Высшая математика III. Функции комплексного переменного. Ряды. Интегральные преобразования

http://edu.tusur.ru/publications/2258 

2. А.П.Ерохина, Л.Н. Байбакова. Высшая математика III в упражнениях с задачами и решениями.

http://narod.ru/disk/29273915001/eroh-bajb.djvu.html

3. А.А.Ельцов, Т.А.Ельцова. Интегральное исчисление и дифференциальные уравнения http://edu.tusur.ru/publications/2259 

4. Практикум по интегральному исчислению и дифференциальным уравнениям: Учебное пособие / Ельцов А. А., Ельцова Т. А. — 2005. 204 с. http://edu.tusur.ru/publications/39

5. Воробьёв Н.Н. Теория рядов. Санкт-Петербург, 2002, изд-во «Лань». ISBN 5-8114-0446-8